Содержание
- 2. Учебные вопросы: Представление целых беззнаковых чисел Представление чисел с фиксированной точкой Операции над числами с фиксированной
- 3. Память состоит из нумерованных ячеек. Линейная структура (адрес ячейки – одно число). Байт – это наименьшая
- 4. Целые беззнаковые числа Беззнаковые данные – не могут быть отрицательными. Для представления беззнаковых чисел может использоваться
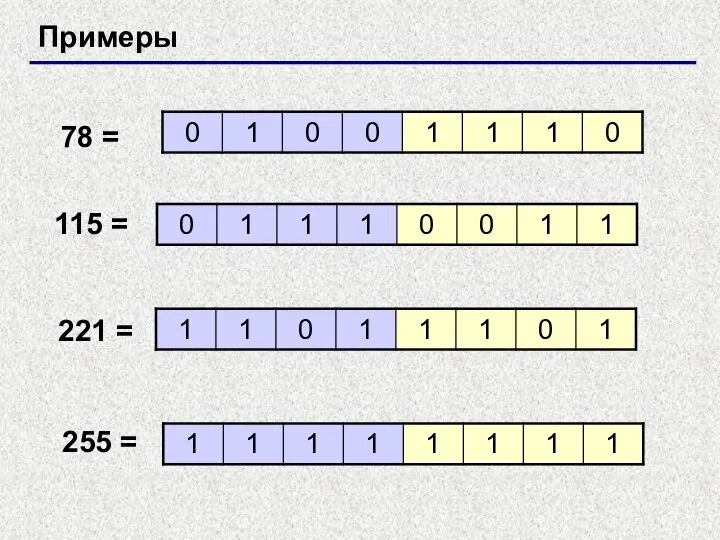
- 5. Примеры 78 = 115 = 221 = 255 =
- 6. Целое без знака размером 2 байта (16 бит) диапазон значений 0…65535, 0…FFFF16 = 216-1 Си: unsigned
- 7. 2. Представление чисел с фиксированной точкой Числа с фиксированной точкой — форма представления вещественных чисел, когда
- 8. Пример 1. Пусть даны числа 123.6, 0.01 и 1.5143. Записать их в виде числа с фиксированной
- 9. Такая форма представления наиболее проста для восприятия, но имеет существенный недостаток: - программирование операций для чисел
- 10. В восьми разрядной сетке числа с фиксированной точкой (байтовые числа) могут быть представлены в диапазоне значений:
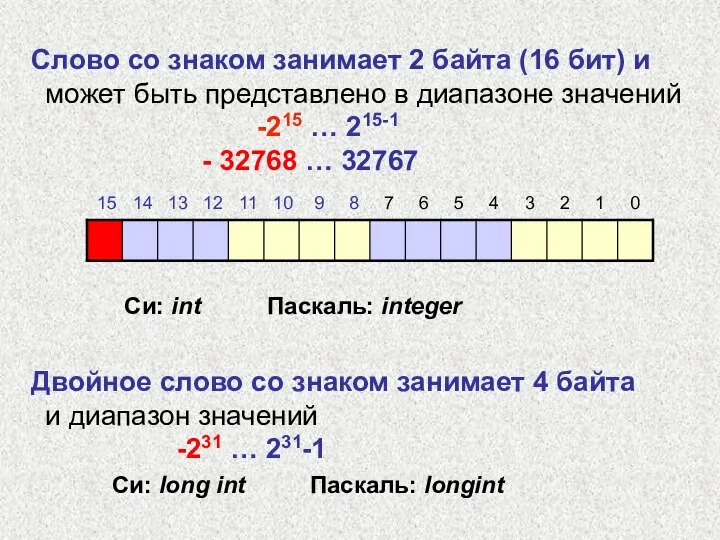
- 11. Слово со знаком занимает 2 байта (16 бит) и может быть представлено в диапазоне значений -215
- 12. 3. Коды чисел и операции над ними
- 13. Такой способ представления числа является наиболее естественным, так как обеспечивает простой переход от двоичной записи числа
- 14. 3.2 Обратный код Обратный код для положительных чисел совпадает с прямым кодом, Обратный код для отрицательных
- 15. Пример представления числа -12310 в обратном коде: 1. Перевод числа -12310 в двоичное число: 2. Запись
- 16. Для обратного кода справедливо следующее соотношение: где xsign – значение знакового разряда, xi – значение i-го
- 17. При использовании обратного кода арифметические операции для отрицательных чисел выполняются проще. Само получение обратных кодов не
- 18. 3.3 Дополнительный код Дополнительный код для положительных чисел совпадает с прямым кодом, Дополнительный код для отрицательных
- 19. Пример представления числа -11510 в дополнительном коде: 1. Перевод числа -11510 в двоичное число: 2. Запись
- 20. Для дополнительного кода справедливо следующее соотношение: где xsign – значение знакового разряда, xi – значение i-го
- 21. Анализ дополнительного кода. - Получение дополнительного кода происходит несколько сложнее, чем обратного. - Использование дополнительного кода
- 22. 3.4 Ошибки выполнения операций над кодами Переполнение разрядной сетки: в результате сложения больших положительных чисел получается
- 23. Перенос: при сложении больших (по модулю) отрицательных чисел получается положительное (перенос за границы разрядной сетки). ДК
- 24. Учебные вопросы для самостоятельного изучения
- 25. 4. Представление чисел с плавающей точкой X = s ⋅ M ⋅ 2e s – знак
- 26. Нормализованные числа в памяти IEEE Standard for Binary Floating-Point Arithmetic (IEEE 754) 15,625 = 1⋅1,1111012 ⋅23
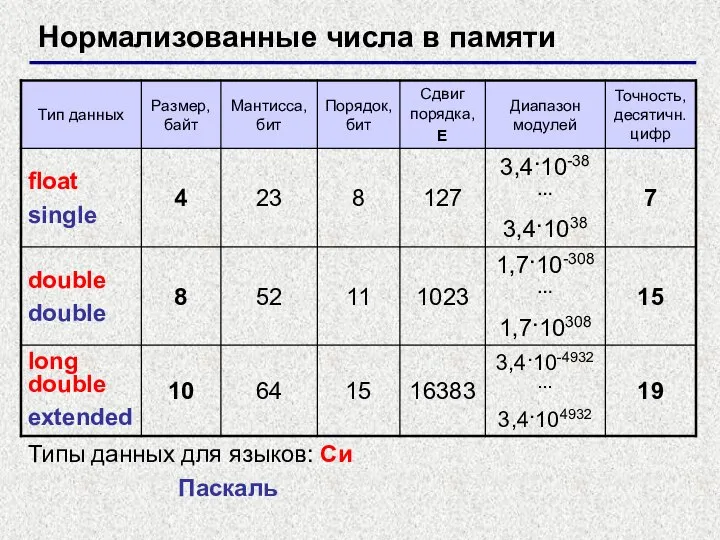
- 27. Нормализованные числа в памяти Типы данных для языков: Си Паскаль
- 28. Вещественные числа в памяти 15,625 = 1,1111012 ⋅23 4 байта = 32 бита p = e+127
- 29. 5. Арифметические операции над числами с плавающей точкой сложение Порядок выравнивается до большего 5,5 = 1,0112⋅22
- 30. вычитание Порядок выравнивается до большего 10,75 = 1,010112⋅23 5,25 = 1,01012 ⋅22 = 0,101012 ⋅23 Мантиссы
- 31. умножение Мантиссы умножаются 7 = 1,112 ⋅ 22 1,1 12 3 = 1,12 ⋅ 21 ×
- 32. деление Мантиссы делятся 17,25 = 1,0001012 ⋅ 24 3 = 1,12 ⋅ 21 1,0001012 : 1,12
- 36. Скачать презентацию






























 Среда программирования programming environment
Среда программирования programming environment Основы программирования на языке Python
Основы программирования на языке Python Практика интервью. Народная журналистика
Практика интервью. Народная журналистика Графический редактор Paint. Планируем последовательность действий
Графический редактор Paint. Планируем последовательность действий Basic Technology Components
Basic Technology Components Основные положения кибернетики. Лекция №1
Основные положения кибернетики. Лекция №1 Сервис оценки столовых УРФУ
Сервис оценки столовых УРФУ Единицы измерения количества информации
Единицы измерения количества информации Структуры данных и алгоритмы. Дружественные классы и функции
Структуры данных и алгоритмы. Дружественные классы и функции Ежегодные мероприятия университета Частного права
Ежегодные мероприятия университета Частного права Программно-аппаратные средства обеспечения информационной безопасности (ПАСО ИБ)
Программно-аппаратные средства обеспечения информационной безопасности (ПАСО ИБ) 6-2-1-kompjuternye-objekty
6-2-1-kompjuternye-objekty Односторонние T-тесты гипотез, относящихся к коэффициентам регрессии
Односторонние T-тесты гипотез, относящихся к коэффициентам регрессии Технологии сегодня
Технологии сегодня Введение в блокчейн
Введение в блокчейн Я имею право на образование
Я имею право на образование Организация запросов в SQL. Запрос на выборку данных из одной таблицы
Организация запросов в SQL. Запрос на выборку данных из одной таблицы ТЗ на визуализацию. Правки
ТЗ на визуализацию. Правки Защита персональных данных
Защита персональных данных Безопасность в Интернете для всей семьи
Безопасность в Интернете для всей семьи АО Концерн Калашниов. 1С:Производственная безопасность. Комплексная
АО Концерн Калашниов. 1С:Производственная безопасность. Комплексная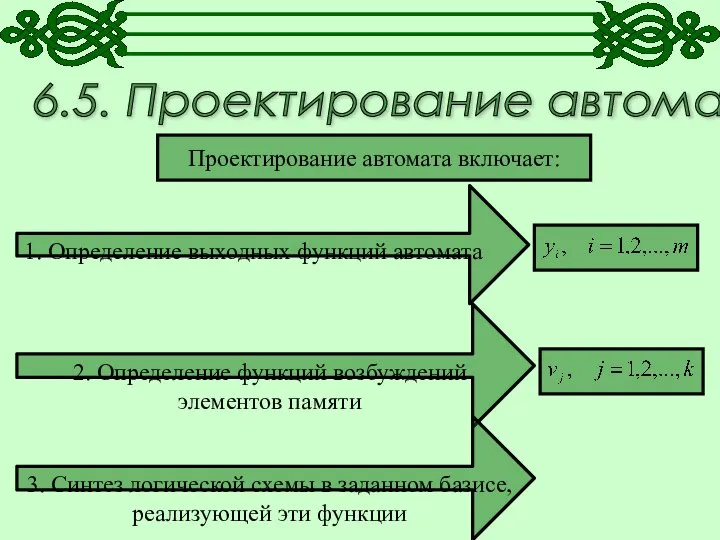 Проектирование автомата
Проектирование автомата Безопасность в Интернете
Безопасность в Интернете Симулятор установки windows 5
Симулятор установки windows 5 Презентация "Алгоритм. Свойства. Способы записи. Линейные алгоритмы" - скачать презентации по Информатике
Презентация "Алгоритм. Свойства. Способы записи. Линейные алгоритмы" - скачать презентации по Информатике Обработка текстовых величин
Обработка текстовых величин лекция 5
лекция 5 Использование встроенного задачника в Pascal ABC
Использование встроенного задачника в Pascal ABC