Logic

Значения
В алгебре логики переменные и выражения могут иметь только два значения:
Истина;
Ложь.
Подобно древнегреческой логике.

Отрицание ¬
Иными словами НЕ. Также обозначается полоской над переменной или функцией.

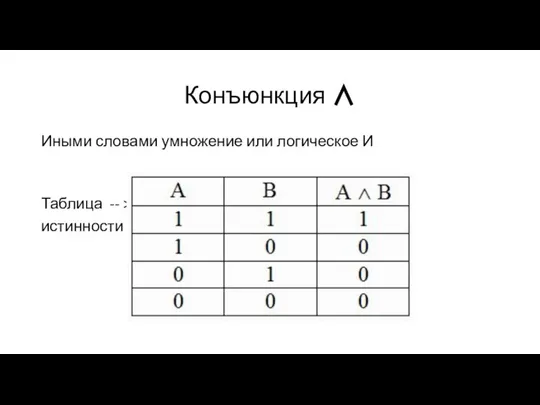
Конъюнкция ∧
Иными словами умножение или логическое И
Таблица -- >
истинности

Дизъюнкция ∨
Иными словами умножение или логическое ИЛИ

Импликация →
Иными словами операция следования. Из истины не может следовать ложь.

Эквивалентность ≡
Если переменные равны, то функция истина.

XOR ⊕
Иными словами “исключающее ИЛИ”.

NB!
Обратите внимание, что таблица истинности XOR соответствует отрицанию эквивалентности. Следовательно A ⊕ B = ¬ (A ≡ B)
А таблица истинности импликации соответствует ¬A ∨ B.
Следовательно: A → B = ¬A ∨ B

Законы
В алгебре логики действуют те же правила, что и в обычной: