Логические основы компьютера

Математический аппарат алгебры логики очень удобен для описания того, как функционируют аппаратные средства компьютера, поскольку основной системой счисления в компьютере является двоичная, в которой используются цифры 1 и 0, а значений логических переменных тоже два: “1” и “0”.
1) одни и те же устройства компьютера могут применяться для обработки и хранения как числовой информации, представленной в двоичной системе счисления, так и логических переменных;
2) на этапе конструирования аппаратных средств алгебра логики позволяет значительно упростить логические функции, описывающие функционирование схем компьютера, и, следовательно, уменьшить число элементарных логических элементов, из десятков тысяч которых состоят основные узлы компьютера.

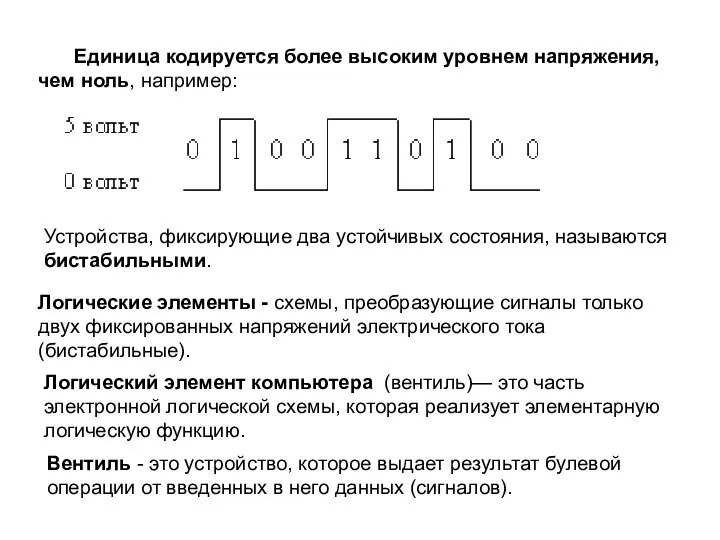
Единица кодируется более высоким уровнем напряжения, чем ноль, например:
Устройства, фиксирующие два устойчивых состояния, называются бистабильными.
Логические элементы - схемы, преобразующие сигналы только двух фиксированных напряжений электрического тока (бистабильные).
Логический элемент компьютера (вентиль)— это часть электронной логичеcкой схемы, которая реализует элементарную логическую функцию.
Вентиль - это устройство, которое выдает результат булевой операции от введенных в него данных (сигналов).

Логические основы устройства компьютера
Преобразование сигнала логическими элементами задаётся таблицей состояний (идентична таблице истинности)
Каждый логический элемент имеет свое условное обозначение, которое выражает его логическую функцию, но не указывает на то, какая именно электронная схема в нем реализована. Это упрощает запись и понимание сложных логических схем.
Логическими элементами компьютеров являются электронные схемы И, ИЛИ, НЕ, И-НЕ , ИЛИ-НЕ, исключающее ИЛИ,
Исключающая ИЛИ-НЕ.

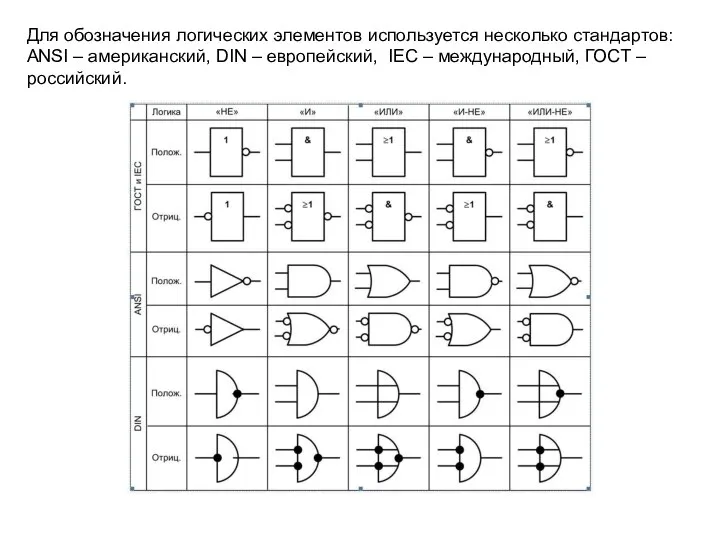
Для обозначения логических элементов используется несколько стандартов: ANSI – американский, DIN – европейский, IEC – международный, ГОСТ – российский.

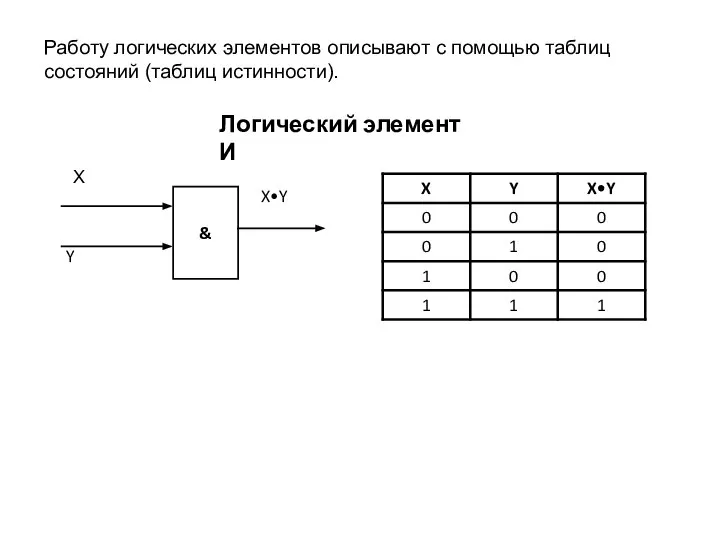
Работу логических элементов описывают с помощью таблиц состояний (таблиц истинности).
Логический элемент И

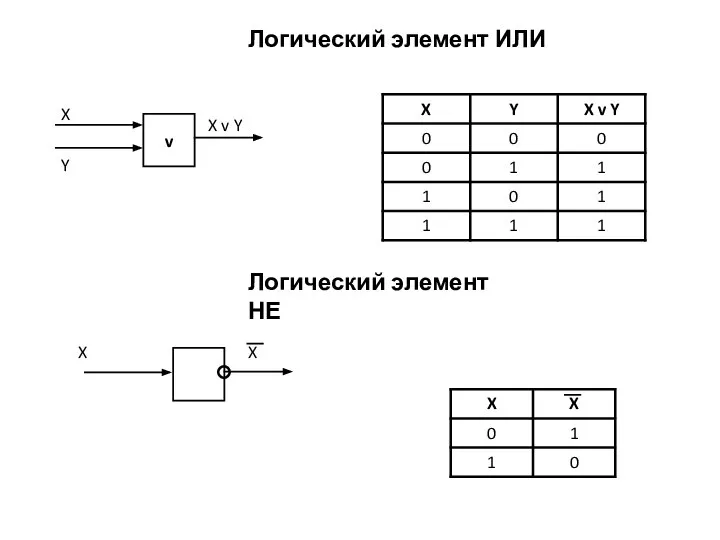
Логический элемент ИЛИ
Логический элемент НЕ

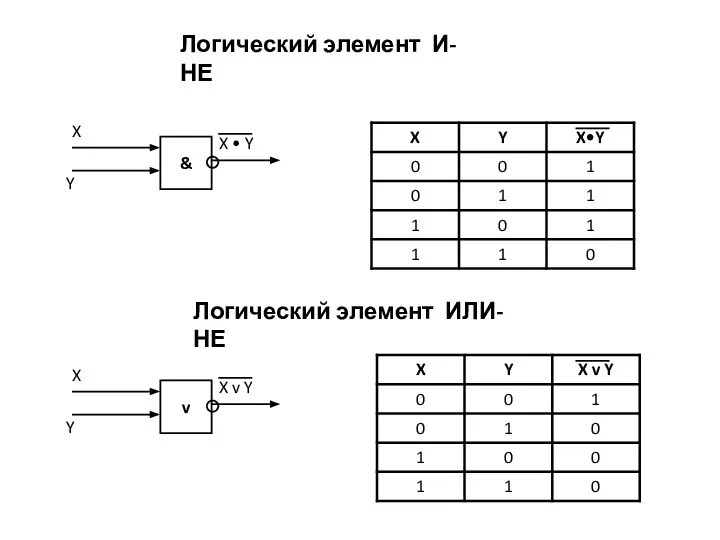
Логический элемент И-НЕ
Логический элемент ИЛИ-НЕ

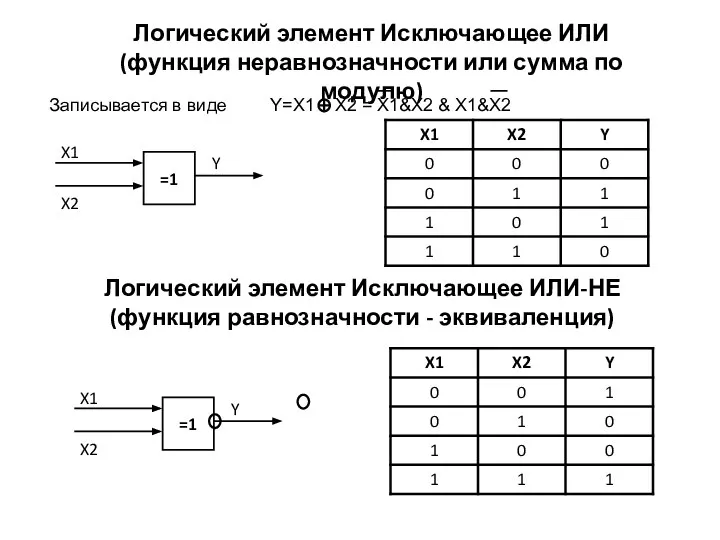
Логический элемент Исключающее ИЛИ
(функция неравнозначности или сумма по модулю)
Записывается в виде
Логический элемент Исключающее ИЛИ-НЕ
(функция равнозначности - эквиваленция)

Интегральные логические элементы выпускаются в стандартных корпусах с 14 или 16 выводами. Один вывод используется для подключения источника питания, еще один является общим для источников сигналов и питания. Оставшиеся 12 (14) выводов используют как входы и выходы логических элементов. В одном корпусе может находится несколько самостоятельных логических элементов.
Цоколевка (нумерация выводов) некоторых микросхем.

Задачи на логические схемы: синтез и анализ логических схем.
Задачи анализа логических схем
Определение функции f, реализуемой заданной логической схемой
Порядок действий:
1. Логическая схема разбивается на ярусы, ярусам присваиваются последовательные номера.
2. Выводы каждого логического элемента обозначаются названием искомой функции, снабжённым цифровым индексом, где первая цифра – номер яруса, а остальные – порядковый номер элемента в ярусе.
3. Для каждого элемента записывается аналитическое выражение, связывающее его выходную функцию с входными переменными. Выражение определяется логической функцией, реализуемой данным логическим элементом.
4. Производится подстановка одних выходных функций через другие, пока не получится булева функция, выраженная через входные переменные.

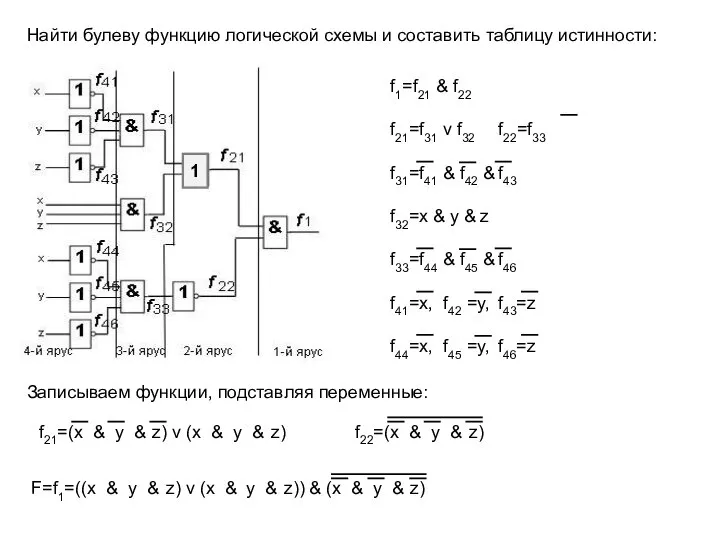
Найти булеву функцию логической схемы и составить таблицу истинности:
f1=f21 & f22
f32=x & y & z
Записываем функции, подставляя переменные:

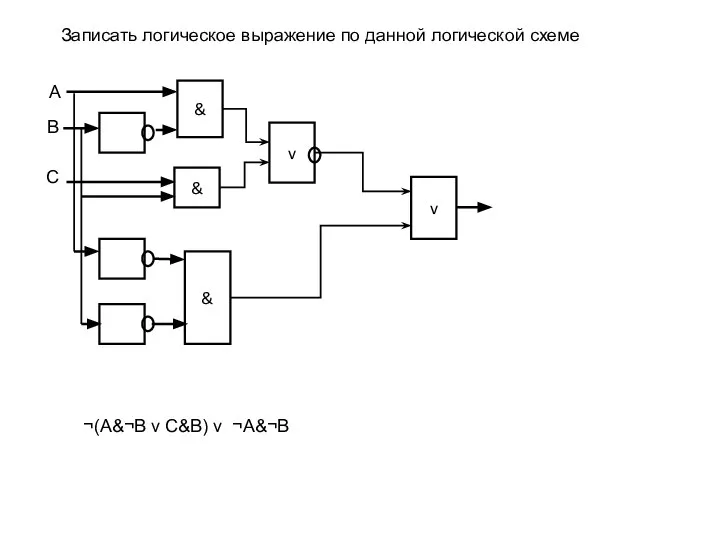
Записать логическое выражение по данной логической схеме
¬(A&¬B v C&B) v ¬A&¬B

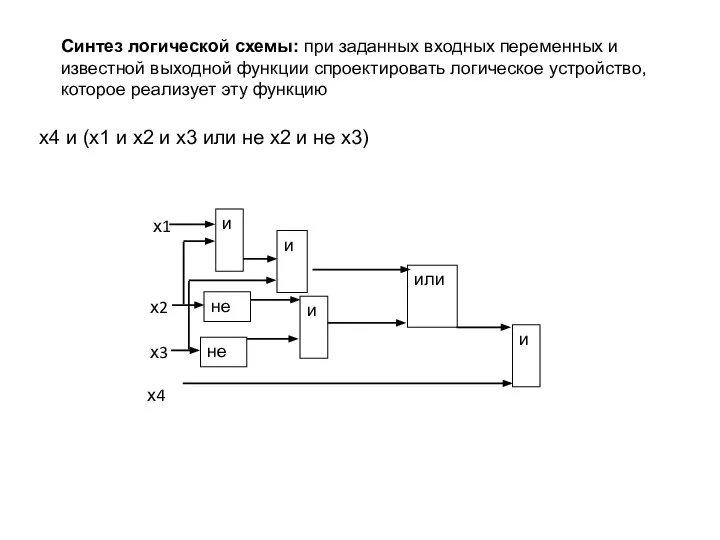
х4 и (х1 и х2 и х3 или не х2 и не х3)
Синтез логической схемы: при заданных входных переменных и известной выходной функции спроектировать логическое устройство, которое реализует эту функцию

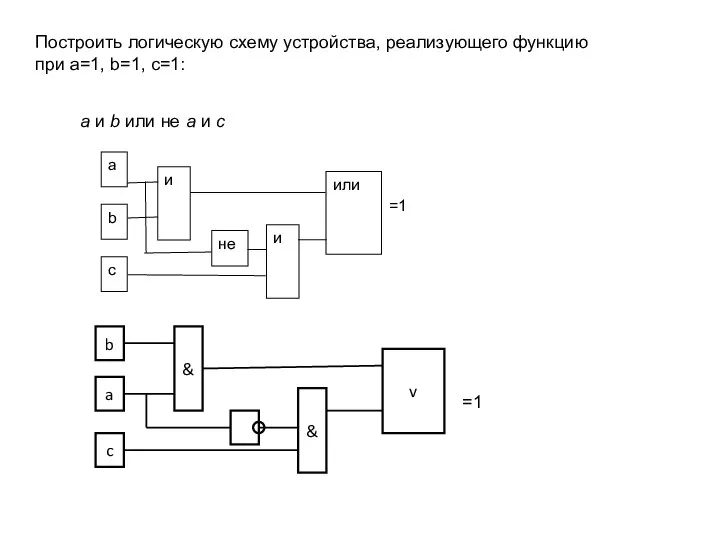
Построить логическую схему устройства, реализующего функцию
при а=1, b=1, с=1:
а и b или не а и с

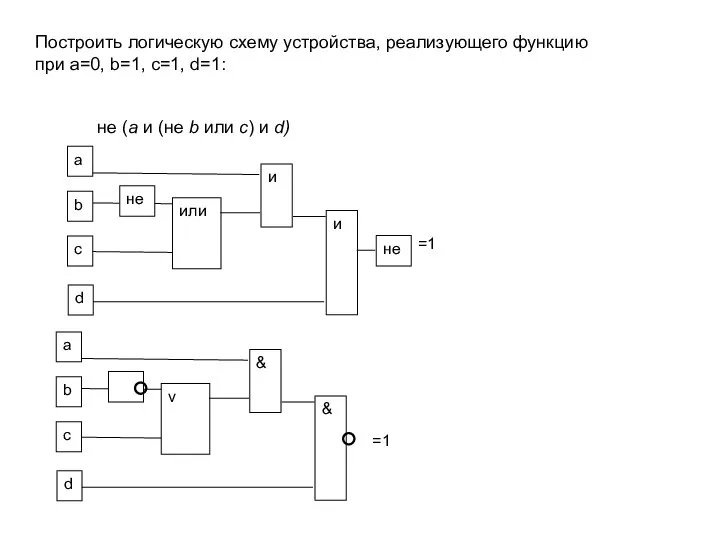
Построить логическую схему устройства, реализующего функцию
при а=0, b=1, с=1, d=1:
не (а и (не b или с) и d)

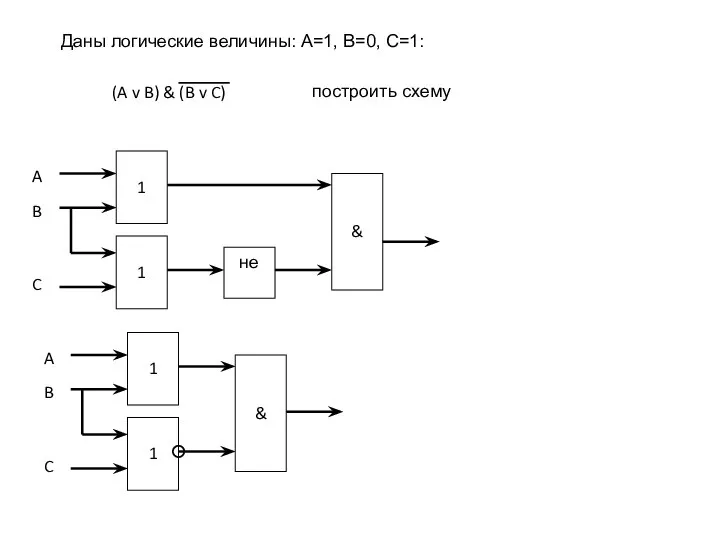
Даны логические величины: A=1, B=0, C=1:
(A v B) & (B v C)
построить схему

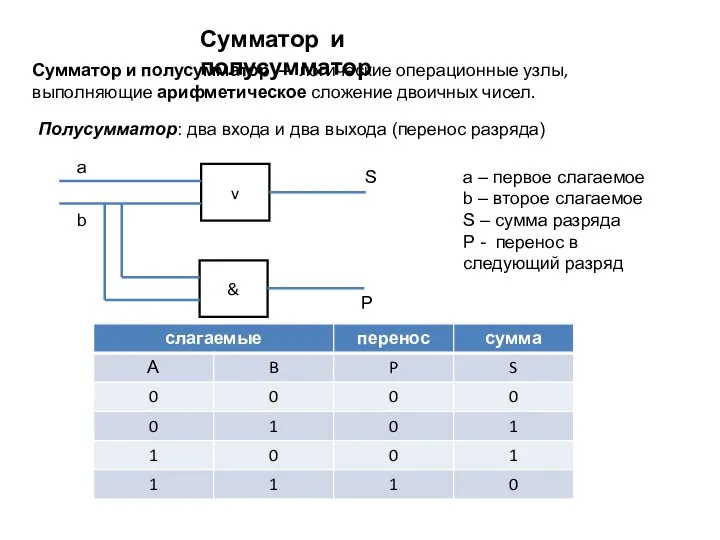
Сумматор и полусумматор
Сумматор и полусумматор — логические операционные узлы, выполняющие арифметическое сложение двоичных чисел.
Полусумматор: два входа и два выхода (перенос разряда)
a – первое слагаемое
b – второе слагаемое
S – сумма разряда
P - перенос в следующий разряд

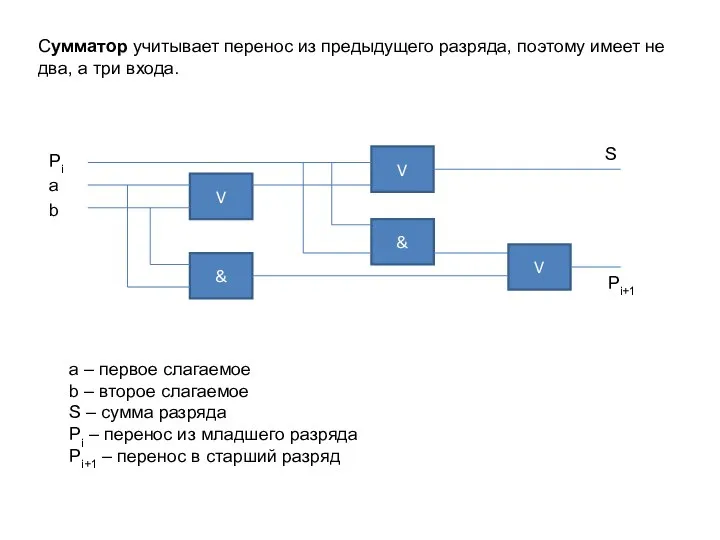
Сумматор учитывает перенос из предыдущего разряда, поэтому имеет не два, а три входа.
&
a – первое слагаемое
b – второе слагаемое
S – сумма разряда
Pi – перенос из младшего разряда
Pi+1 – перенос в старший разряд

По количеству одновременно обрабатываемых разрядов складываемых чисел:
одноразрядные
многоразрядные.
По числу входов и выходов одноразрядных двоичных сумматоров:
Многоразрядный двоичный сумматор предназначен для сложения многоразрядных двоичных чисел и представляет собой комбинацию одноразрядных сумматоров,
четвертьсумматоры
полусумматоры (2 входа, 2 выхода: реализует арифметическую сумму в данном разряде, перенос в следующий разряд);
полные одноразрядные двоичные сумматоры (3 входа, 2 выхода: аналогично полусумматору).

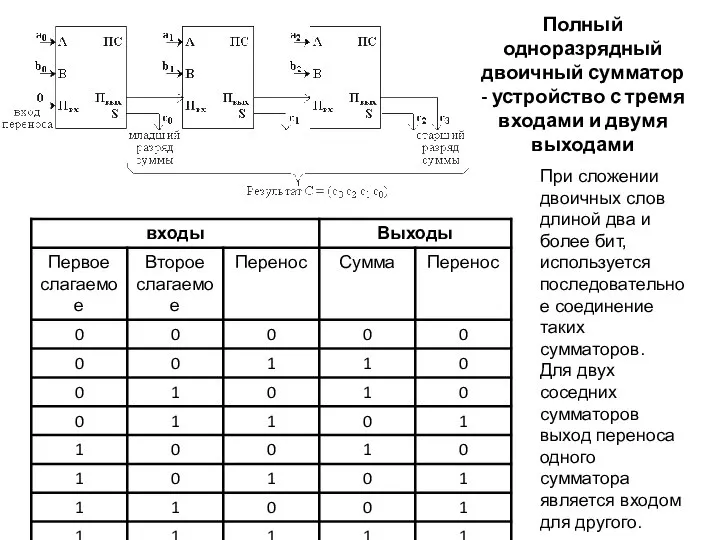
Полный одноразрядный двоичный сумматор - устройство с тремя входами и двумя выходами
При сложении двоичных слов длиной два и более бит, используется последовательное соединение таких сумматоров.
Для двух соседних сумматоров выход переноса одного сумматора является входом для другого.

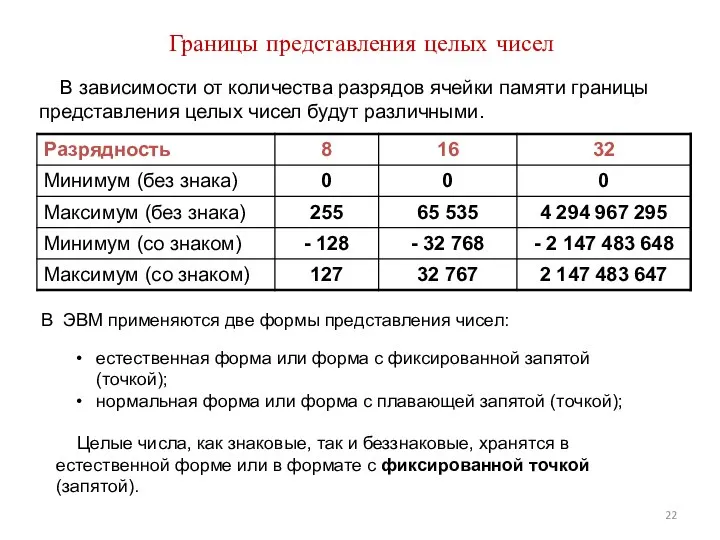
Границы представления целых чисел
В зависимости от количества разрядов ячейки памяти границы представления целых чисел будут различными.
Целые числа, как знаковые, так и беззнаковые, хранятся в естественной форме или в формате с фиксированной точкой (запятой).
В ЭВМ применяются две формы представления чисел:
естественная форма или форма с фиксированной запятой (точкой);
нормальная форма или форма с плавающей запятой (точкой);

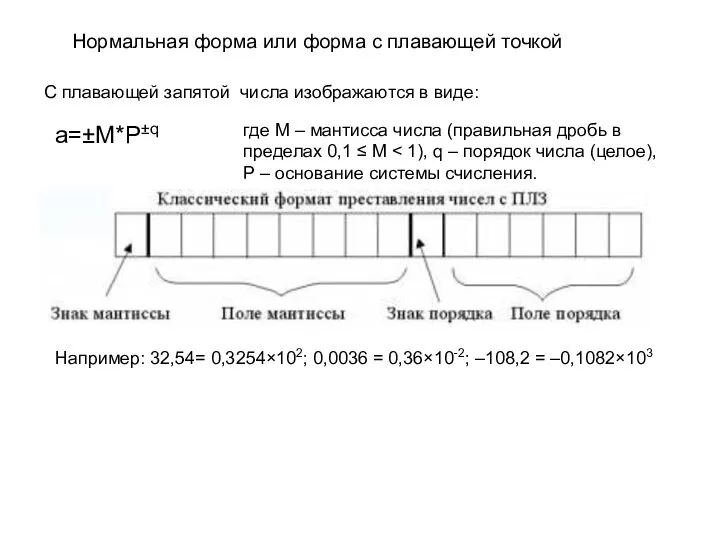
Нормальная форма или форма с плавающей точкой
С плавающей запятой числа изображаются в виде:
а=±М*Р±q
где М – мантисса числа (правильная дробь в пределах 0,1 ≤ М < 1), q – порядок числа (целое), Р – основание системы счисления.
Например: 32,54= 0,3254×102; 0,0036 = 0,36×10-2; –108,2 = –0,1082×103

Решить:
1. Привести к нормализованному виду числа, оставляя их в тех же системах счисления, в которых они записаны:
а) –0. 0000010111012; в) 100.012;
б) 98765432110; г) –0. 0015028;
2. Запишите в естественной форме с фиксированной запятой следующие нормализованные числа:
а) 0. 10112 •21; б) 0. 10112 •211;
в) 0. 1234510 •10-3; г) –0. 400658 •8-4;

Экспоненциальная запись представляют в виде MEp, где:
M — мантисса,
E (exponent), означающая «*10^» («…умножить на десять в степени…»),
p — порядок.
Например:
1, 602176565Е -19= 1, 602176565·10-19 (элементарный заряд)
Экспоненциальный формат
Научный (SCIENTIFIC) формат :
- для мантиссы M должно выполняться неравенство 0 < |M| < 1;
- значение порядка P любое целое.
Инженерный (ENGINERING) формат:
- мантисса M формируется с целой и дробной (если необходимо) частями, причем целая часть содержит не более трех значащих цифр так, чтобы значение порядка P было равным максимальному возможному числу, кратному трем.
Например, дано число 31450000:
научный формат: экспоненциальная запись 0,3145Е8
инженерный формат: экспоненциальная запись 31,45Е6
1,380648524Е -23= 1,380648524·10-23 (Постоянная Больцмана)
6,02214129е23 = 6,02214129·1023 (число Авогадро)

Решить:
1) 3,567Е-6=
0,000003567
2) 3,567Е9=
3567000000
3) 749200000000=
7,492е11
4) 0,000000000012=
1,2е-11
=0,7492е12
=74,92е10
=12,0е-12
=0,12е-10

Максимальное знаковое число 127
Минимальное знаковое число -128
Максимальное
255
Прямой код;
Обратный код;
Дополнительный код
Отрицательные целые числа представляются в ЭВМ с помощью дополнительного кода.
Например: записать дополнительный код отрицательного числа -2002 для 16-разрядного компьютерного представления.
Прямой код: |-200210|=200210=00000111110100102
Обратный код: 11111000001011012
Дополнительный код: 11111000001011102