Слайд 3Поначалу булева алгебра не имела никакого практического значения. Однако уже в XX

веке ее положения нашли применение в разработке различных электронных схем. Законы и аппарат алгебры логики стали использоваться при проектировании различных частей компьютеров (память, процессор).
Слайд 4Алгебра логики оперирует с высказываниями. Под высказыванием понимают повествовательное предложение, относительно которого

имеет смысл говорить, истинно оно или ложно. Над высказываниями можно производить определенные логические операции, в результате которых получаются новые высказывания. Наиболее часто используются логические операции, выражаемые словами «не», «и», «или».
Слайд 5Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты

вычислений сложных высказываний при различных значениях исходных простых высказываний. Простые высказывания обозначаются переменными (например, A и B).
Слайд 6Конъюнкция (логическое умножение)
Конъюнкция (логическое умножение)
Сложное высказывание А & В истинно только в
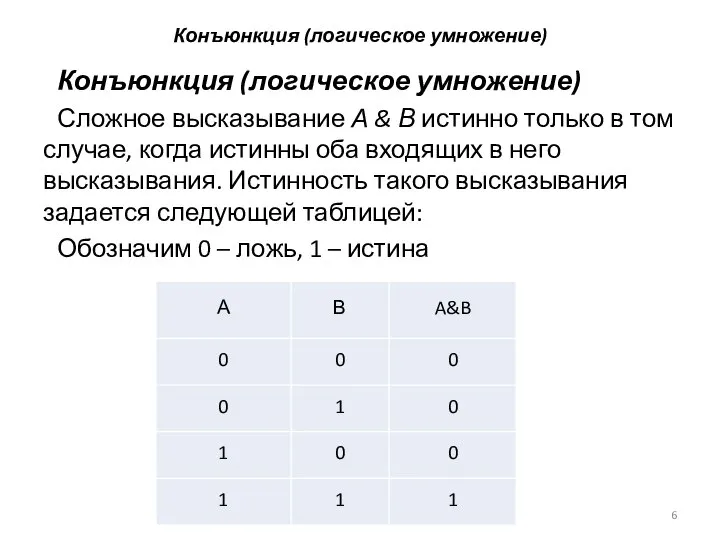
том случае, когда истинны оба входящих в него высказывания. Истинность такого высказывания задается следующей таблицей:
Обозначим 0 – ложь, 1 – истина
Слайд 7Дизъюнкция (логическое сложение)
Дизъюнкция (логическое сложение)
Сложное высказывание A ∨ В истинно, если истинно
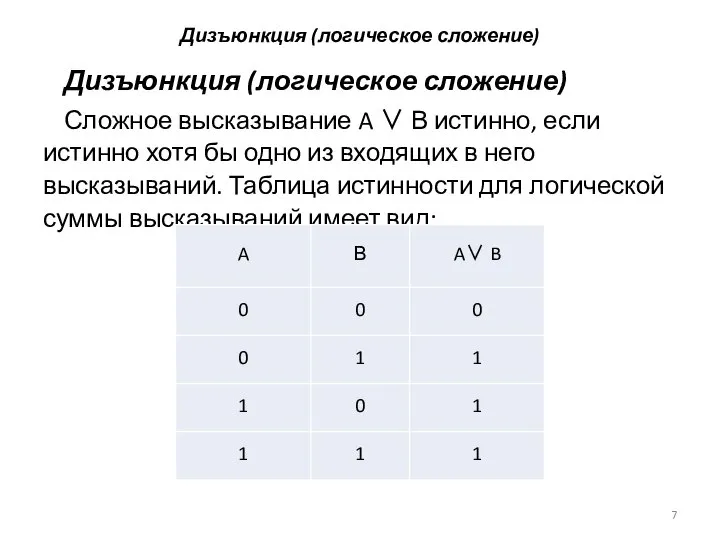
хотя бы одно из входящих в него высказываний. Таблица истинности для логической суммы высказываний имеет вид:
Слайд 8Инверсия (логическое отрицание)
Инверсия (логическое отрицание)
Присоединение частицы НЕ (NOT) к данному высказыванию называется

операцией отрицания (инверсии). Она обозначается Ā (или ¬А)и читается не А . Если высказывание А истинно, то В ложно, и наоборот. Таблица истинности в этом случае имеет вид:
Слайд 9Обозначения логических операций И, ИЛИ и НЕ в классической математической логике (∨,∧,

¬) интуитивно непонятны, не проявляют аналогии с обычной алгеброй.
Альтернативные обозначения «НЕ» — черта сверху;
«И» — знак умножения (логическое умножение);
«ИЛИ» — знак «+» (логическое сложение).
Слайд 10Продемонстрируем мощь альтернативных обозначений логических операций:

Слайд 11Примеры логических операций
ИСТИНА ЛОЖЬ
а = гласная а = согласная
А = НЕ

согласная А = НЕ гласная
(А = гласная) И (О = гласная) (А = гласная) И (З = гласная)
(А = гласная) ИЛИ (З = гласная) (А = согласная) ИЛИ (З = гласная)










 Предметно-ориентированное проектирование автоматизированных систем управления
Предметно-ориентированное проектирование автоматизированных систем управления Виконання операцій з надання послуг копіювального центру. Робота з принтером
Виконання операцій з надання послуг копіювального центру. Робота з принтером Компьютерные сети. Тема 4
Компьютерные сети. Тема 4 Компьютерное проектирование - 6
Компьютерное проектирование - 6 Графические информационные модели. Моделирование и формализация
Графические информационные модели. Моделирование и формализация Печатать ПРЕЗЕНТАЦИЯ
Печатать ПРЕЗЕНТАЦИЯ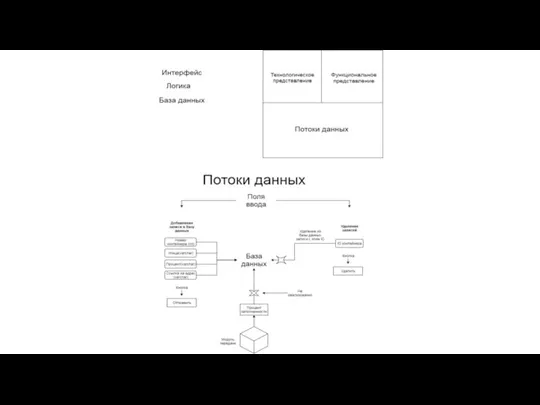 Потоки данных
Потоки данных Скриншот история подключений
Скриншот история подключений Компьютерная игра, где могут играть 4 игрока, используя 1 компьютер
Компьютерная игра, где могут играть 4 игрока, используя 1 компьютер Почти графический редактор
Почти графический редактор JavaScript
JavaScript Лекция 13
Лекция 13 Оказание телемедицинских услуг в режиме онлайн. Руководство пользователя Lime Team
Оказание телемедицинских услуг в режиме онлайн. Руководство пользователя Lime Team Урок информатики, 7 класс
Урок информатики, 7 класс Создаем игру Fifa
Создаем игру Fifa Правила этикета в сети интернета
Правила этикета в сети интернета Мы на airbnb. Онлайн-площадка для размещения, поиска и краткосрочной аренды частного жилья по всему миру
Мы на airbnb. Онлайн-площадка для размещения, поиска и краткосрочной аренды частного жилья по всему миру Система типов C#
Система типов C# Медиация в моей жизни
Медиация в моей жизни Устройства памяти компьютера. Информатика в школе
Устройства памяти компьютера. Информатика в школе Аналитика на YouTube. Обзоры от Арстайл
Аналитика на YouTube. Обзоры от Арстайл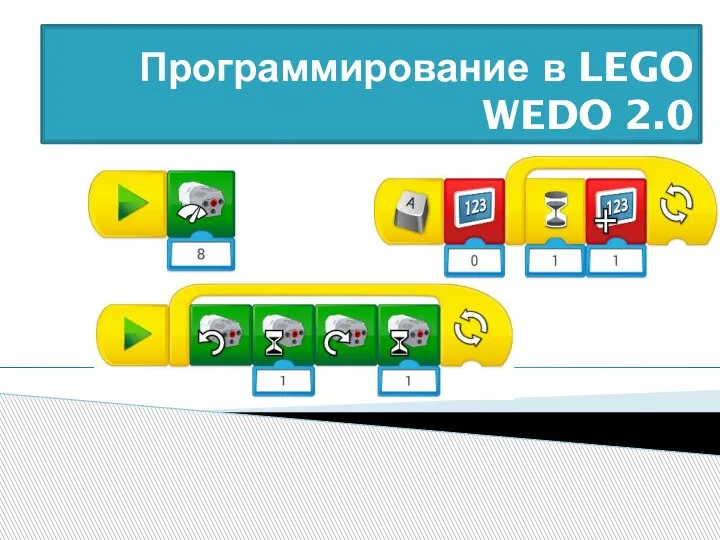 Программирование в Lego Wedo 2.0
Программирование в Lego Wedo 2.0 Шрифты. Структура тега
Шрифты. Структура тега Электронный документооборот
Электронный документооборот Мастер класс/ Как подобрать мобильное приложение для урока
Мастер класс/ Как подобрать мобильное приложение для урока Matlab Simulink. Окно обозревателя разделов библиотеки
Matlab Simulink. Окно обозревателя разделов библиотеки Введение в SAS Enterprise Guide
Введение в SAS Enterprise Guide Разработка рекомендация по техническому обслуживанию сетевых серверов
Разработка рекомендация по техническому обслуживанию сетевых серверов