Слайд 2ЦЕЛИ ОБУЧЕНИЯ
ПЕРЕВОДИТЬ ЦЕЛЫЕ ЧИСЛА ИЗ ДЕСЯТИЧНОЙ СИСТЕМЫ СЧИСЛЕНИЯ В ДВОИЧНУЮ, ВОСЬМЕРИЧНУЮ, ШЕСТНАДЦАТЕРИЧНУЮ

И ОБРАТНО;
ИСПОЛЬЗОВАТЬ ЛОГИЧЕСКИЕ ОПЕРАЦИИ (ДИЗЪЮНКЦИЯ, КОНЪЮНКЦИЯ, ИНВЕРСИЯ);
• СТРОИТЬ ТАБЛИЦЫ ИСТИННОСТИ ДЛЯ ЗАДАННОГО ЛОГИЧЕСКОГО ВЫРАЖЕНИЯ;
• ОБЪЯСНЯТЬ НАЗНАЧЕНИЕ ОСНОВНЫХ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ: КОНЪЮНКТОР, ДИЗЪЮНКТОР, ИНВЕРТОР;
• ПРЕОБРАЗОВЫВАТЬ ЛОГИЧЕСКИЕ ВЫРАЖЕНИЯ В ЛОГИЧЕСКИЕ СХЕМЫ И НАОБОРОТ;
• ОПИСЫВАТЬ ФУНКЦИИ УСТРОЙСТВА УПРАВЛЕНИЯ, АРИФМЕТИКОЛОГИЧЕСКОГО УСТРОЙСТВА И РЕГИСТРОВ ПАМЯТИ КАК ОТДЕЛЬНЫХ ЧАСТЕЙ ПРОЦЕССОРА;
• СРАВНИВАТЬ ТАБЛИЦЫ КОДИРОВКИ СИМВОЛОВ UNICODE И AS
Слайд 3ЛОГИКА – ЭТО НАУКА О ВИДАХ И ЗАКОНАХ ЧЕЛОВЕЧЕСКОГО МЫШЛЕНИЯ, В ТОМ

ЧИСЛЕ О ЗАКОНОМЕРНОСТЯХ ВЫСКАЗЫВАНИЙ, КОТОРЫЕ МОЖНО ДОКАЗАТЬ. КАК НАУЧНЫЕ ДИСЦИПЛИНЫ СФОРМИРОВАНЫ ФОРМАЛЬНАЯ, МАТЕМАТИЧЕСКАЯ, ВЕРОЯТНОСТНАЯ И ДР. ВИДЫ ЛОГИКИ.
ФОРМАЛЬНАЯ ЛОГИКА – ЭТО ЛОГИКА, СВЯЗАННАЯ С АНАЛИЗОМ НАШЕГО СОДЕРЖАТЕЛЬНОГО МНЕНИЯ, КОТОРОЕ ВЫРАЖАЕТСЯ ЯЗЫКОМ РЕЧИ.
ВЕРОЯТНОСТНАЯ ЛОГИКА – ЛОГИКА, СОЗДАВАЕМАЯ СЛУЧАЙНЫМИ ПАРАМЕТРАМИ, ОСНОВАННАЯ НА ИСПОЛЬЗОВАНИИ НЕСКОЛЬКИХ СЕРИЙ ИСПЫТАНИЙ.
Слайд 4МАТЕМАТИЧЕСКАЯ ЛОГИКА ЯВЛЯЕТСЯ ЧАСТЬЮ ФОРМАЛЬНОЙ ЛОГИКИ, ИМЕЕТ ЧЕТКО ОПРЕДЕЛЕННЫЕ ФОРМЫ И ВЫСКАЗЫВАНИЯ.

ОНА ИЗУЧАЮТ ТОЛЬКО ТЕ МЫСЛИ, КОТОРЫЕ МОЖНО РЕШИТЬ ИХ ИСТИННОСТЬ ИЛИ ЛОЖЬ.
ВЫСКАЗЫВАНИЕ – КАКОЕ-ЛИБО ПРЕДПОЛОЖЕНИЕ, КОТОРОЕ МОЖЕТ БЫТЬ ИСТИНОЙ ИЛИ ЛОЖЬЮ. НАПРИМЕР, ВЫСКАЗЫВАНИЯ «НУР-СУЛТАН – СТОЛИЦА РЕСПУБЛИКИ КАЗАХСТАН» И «2 * 3 = 6» – ИСТИННЫЕ, А ТАКИЕ, КАК «ГОРА ПЛОСКАЯ», «2 * 2 = 5» – ЛОЖНЫЕ.
Слайд 5ТАБЛИЦА ИСТИННОСТИ – ЭТО ПРЕДСТАВЛЕНИЕ ЛОГИЧЕСКИХ ОПЕРАЦИЙ В ВИДЕ ТАБЛИЦЫ, В КОТОРОЙ

ВСЕ ВОЗМОЖНЫЕ ПОСЛЕДОВАТЕЛЬНОСТИ ЗНАЧЕНИЙ ИСТИННОСТИ ВСТРОЕННЫХ ОПЕРАНД ПЕРЕЧИСЛЕНЫ ВМЕСТЕ С ФАКТИЧЕСКИМ ЗНАЧЕНИЕМ РЕЗУЛЬТАТА ОПЕРАЦИИ ДЛЯ КАЖДОЙ ИЗ ЭТИХ ПОСЛЕДОВАТЕЛЬНОСТЕЙ.
Слайд 6ɅОГИЧЕСКОЕ УМНОЖЕНИЕ (КОНЪЮНКЦИЯ)
СОЕДИНЕНИЕ ДВУХ ПРОСТЫХ ВЫСКАЗЫВАНИЙ A И B В ОДНО СОСТАВНОЕ

С ПОМОЩЬЮ СОЮЗА И НАЗЫВАЕТСЯ ЛОГИЧЕСКИМ УМНОЖЕНИЕМ, ИЛИ КОНЪЮНКЦИЕЙ, А РЕЗУЛЬТАТ ОПЕРАЦИИ – ЛОГИЧЕСКИМ ПРОИЗВЕДЕНИЕМ. ОПЕРАЦИЯ И ОТМЕЧАЕТСЯ ЗНАКОМ «‸», «·» ИЛИ «&».
Слайд 7ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОЙ ОПЕРАЦИИ И.
Здесь А и В – два высказывания, принимающие
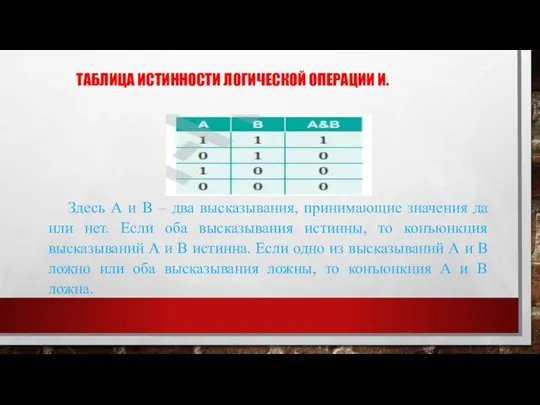
значения да или нет. Если оба высказывания истинны, то конъюнкция высказываний А и В истинна. Если одно из высказываний А и В ложно или оба высказывания ложны, то конъюнкция А и В ложна.
Слайд 8
ɅОГИЧЕСКОЕ СЛОЖЕНИЕ (ДИЗЪЮНКЦИЯ)
ОБЪЕДИНЕНИЕ ДВУХ ПРОСТЫХ УТВЕРЖДЕНИЙ A И B В ОДНО СОСТАВНОЕ

УТВЕРЖДЕНИЕ С ПОМОЩЬЮ СОЮЗА ИЛИ НАЗЫВАЕТСЯ ЛОГИЧЕСКИМ СЛОЖЕНИЕМ, ИЛИ ДИЗЪЮНКЦИЕЙ, А РЕЗУЛЬТАТ ОПЕРАЦИИ – ЛОГИЧЕСКОЙ СУММОЙ. ОПЕРАЦИЯ ИЛИ ОТМЕЧАЕТСЯ ЗНАКОМ «|», «V» ИЛИ «+». ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОЙ ОПЕРАЦИИ ИЛИ.
Слайд 9
ЕСЛИ ОДНО ИЗ ВЫСКАЗЫВАНИЙ А И В ИСТИННО, ТО ДИЗЪЮНКЦИЯ А И
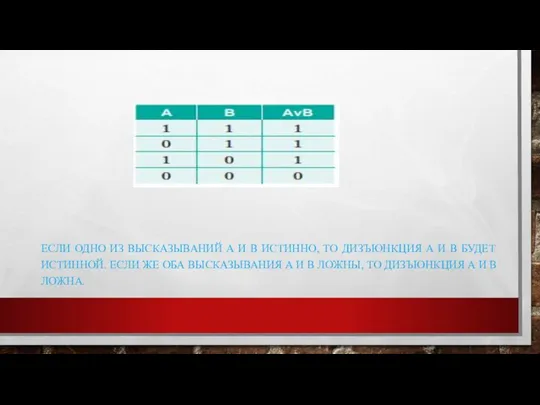
В БУДЕТ ИСТИННОЙ. ЕСЛИ ЖЕ ОБА ВЫСКАЗЫВАНИЯ А И В ЛОЖНЫ, ТО ДИЗЪЮНКЦИЯ А И В ЛОЖНА.
Слайд 10ɅОГИЧЕСКОЕ ОТРИЦАНИЕ (ИНВЕРСИЯ)
ПРИСВОЕНИЕ СОЮЗА НЕ ПРОСТОМУ УТВЕРЖДЕНИЮ A НАЗЫВАЕТСЯ ЛОГИЧЕСКИМ ОТРИЦАНИЕМ,

ИЛИ ИНВЕРСИЕЙ, В РЕЗУЛЬТАТЕ ВЫПОЛНЕНИЯ ЭТОЙ ОПЕРАЦИИ ПОЯВЛЯЕТСЯ НОВОЕ УТВЕРЖДЕНИЕ. ОПЕРАЦИЯ НЕ ОБОЗНАЧАЕТСЯ ЧЕРТОЙ НАД УТВЕРЖДЕНИЕМ А ИЛИ ЗНАКОМ «¬». ТАБЛИЦА ИСТИННОСТИ ЛОГИЧЕСКОЙ ОПЕРАЦИИ НЕ.
Слайд 11ЕСЛИ ИСХОДНОЕ ВЫСКАЗЫВАНИЕ ЛОЖНО, ТОГДА ОТРИЦАНИЕ ЯВЛЯЕТСЯ ИСТИННЫМ, И НАОБОРОТ, ЕСЛИ ИСХОДНОЕ
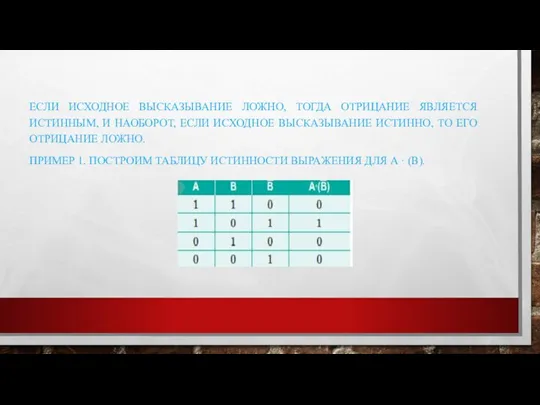
ВЫСКАЗЫВАНИЕ ИСТИННО, ТО ЕГО ОТРИЦАНИЕ ЛОЖНО.
ПРИМЕР 1. ПОСТРОИМ ТАБЛИЦУ ИСТИННОСТИ ВЫРАЖЕНИЯ ДЛЯ А · (В).










 Семантика HTML 5
Семантика HTML 5 Data Science. Ярмарка вакансий
Data Science. Ярмарка вакансий Табличный процессор Excel
Табличный процессор Excel Образование на основе онлайновых социальных сетей
Образование на основе онлайновых социальных сетей Презентация на тему Время и числовая информация (2 класс)
Презентация на тему Время и числовая информация (2 класс)  Диапазоны частот, в которых специальная техника должна обеспечивать измерения. Средства защиты информации
Диапазоны частот, в которых специальная техника должна обеспечивать измерения. Средства защиты информации Источники дохода от арбитража трафика
Источники дохода от арбитража трафика Машинное обучение
Машинное обучение Электронная вычислительная машина
Электронная вычислительная машина Представление цифровой информации в компьютере
Представление цифровой информации в компьютере Организация процесса конструирования
Организация процесса конструирования Понятие информации в теории Шеннона
Понятие информации в теории Шеннона Основы логики
Основы логики Десятичная система счисления
Десятичная система счисления Массив независимых дисков с избыточностью (RAID)
Массив независимых дисков с избыточностью (RAID) Информация для родителей. Безопасный интернет
Информация для родителей. Безопасный интернет Анализ проблемы и моделирование предметной области с использованием системного подхода
Анализ проблемы и моделирование предметной области с использованием системного подхода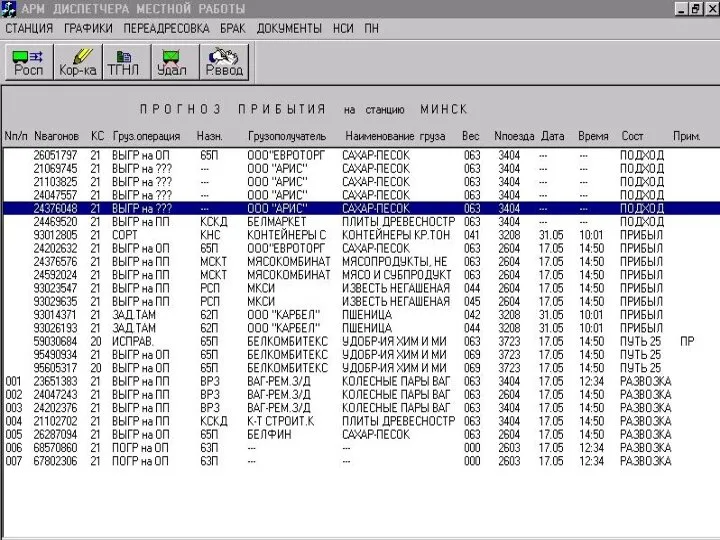 Описание и работа автоматизированной системы управления сортировочной станцией. Формы АРМ ДСЦМ
Описание и работа автоматизированной системы управления сортировочной станцией. Формы АРМ ДСЦМ Виды склеек
Виды склеек Устройство ПК
Устройство ПК Достижение целевого показателя
Достижение целевого показателя Начало 3 лабораторной. Часть 1: Рисование
Начало 3 лабораторной. Часть 1: Рисование Одномерные массивы
Одномерные массивы Skype. Позвони писателю
Skype. Позвони писателю Компьютерные сети. Тема 4
Компьютерные сети. Тема 4 Тест по табличному процесору Excel
Тест по табличному процесору Excel Текстовая информация. Ключевые слова
Текстовая информация. Ключевые слова Доработки применения КТРУ на версию 9.3
Доработки применения КТРУ на версию 9.3