Слайд 2
Логика – наука о законах и формах мышления

Слайд 3Мыслить логично – т.е.
Точно и последовательно
Не допускать противоречий
Уметь вскрывать логические ошибки

Слайд 4Основатель логики
Философ Аристотель
Систематизировал формы и правила мышления.
Исследовал категории «понятие» и «суждение».
Разработал

теорию умозаключений и доказательств.
Сформулировал основные законы мышления.
Слайд 5Логика – является наукой о способах доказательств и опровержений.
Начало исследований в

области логики
было положено Аристотелем в 4 в. до н.э.
Однако математические подходы к этим
вопросам впервые были указаны
Джорджем Булем.В честь него алгебру
высказываний называют “булевой алгеброй”.
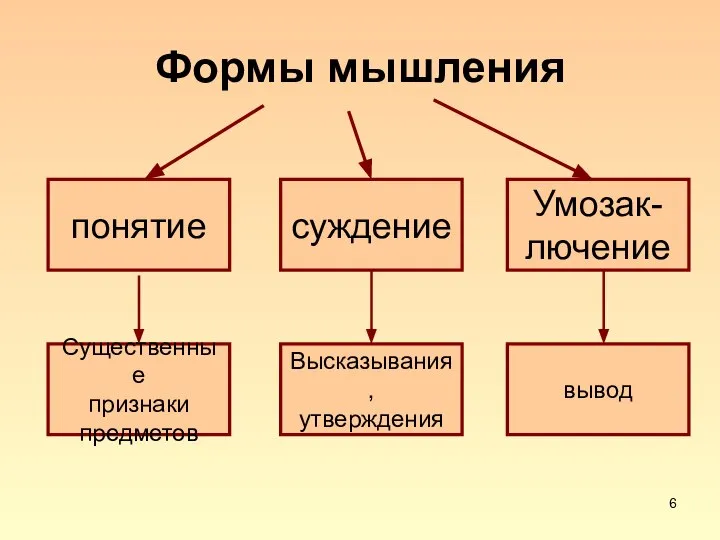
Слайд 6Формы мышления
понятие
суждение
Умозак-
лючение
Существенные
признаки
предметов
Высказывания,
утверждения
вывод
Слайд 7Алгебра логики
Это алгебра высказываний – раздел математической логики, изучающий строение (формулы, структуру)

сложных логических высказываний и способы установления их истинности с помощью алгебраических методов.
Слайд 8Высказывание
Повествовательное предложение, о котором можно сказать истинно оно или ложно.
Например,
Все ученики

– отличники. – ВЛ
Некоторые ученики – отличники. – ВИ
Петя – отличник! – не В
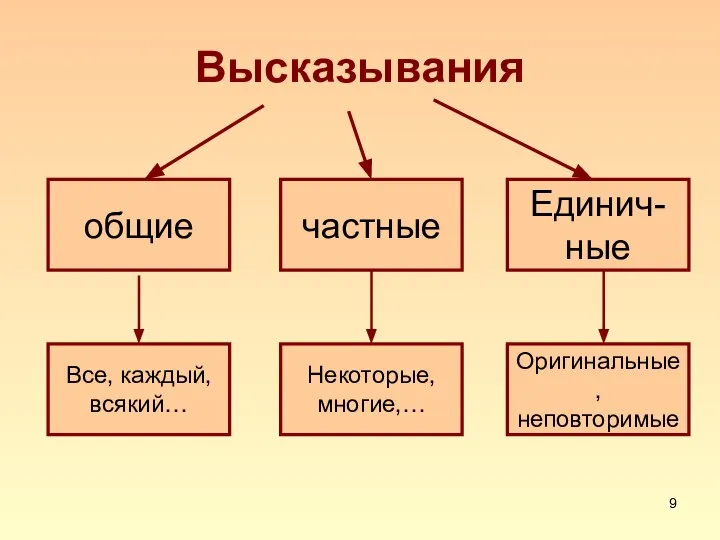
Слайд 9Высказывания
общие
частные
Единич-
ные
Все, каждый,
всякий…
Некоторые,
многие,…
Оригинальные,
неповторимые
Слайд 10Термины
Логические величины – это понятия выражаемые словами И или Л.
Логическая переменная

– это символически выраженная логическая величина.
Логическое выражение – это простое или сложное высказывание, о котором можно сказать И оно или Л.
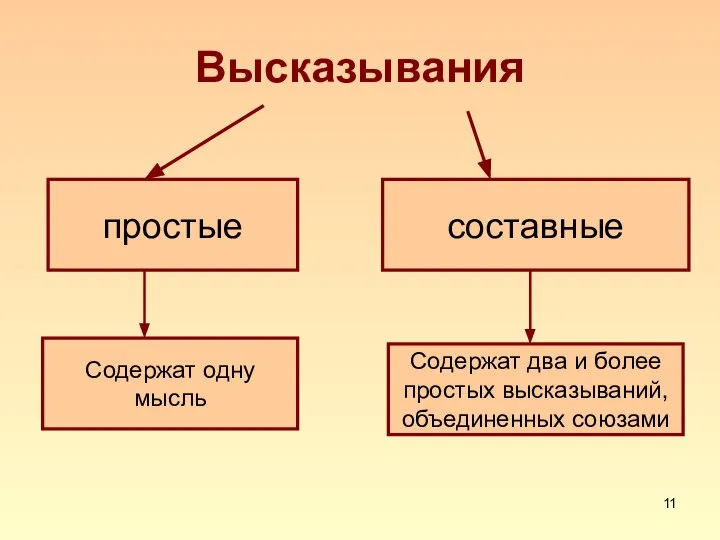
Слайд 11Высказывания
простые
составные
Содержат одну мысль
Содержат два и более
простых высказываний,
объединенных союзами
Слайд 13Инверсия (отрицание)
не А;
неверно, что А
А, А, А
Например,
А – На улице тепло.
не А

– Неверно, что на улице тепло.
Слайд 14Конъюнкция
Логическое умножение.
F(A,B)=А и В
F(A,B)=А * В
F(A,B)=А & В
F(A,B)=А В
F(A,B)=А and В
Например,
А

– У меня есть деньги на покупку машины.
В – У меня есть желание на покупку машины.
Слайд 15Дизъюнкция
Логическое сложение.
F(A,B)=А или В
F(A,B)=А + В
F(A,B)=А В
F(A,B)=А or В
F(A,B)=А | В
Например,
А –

Я пойду на дискотеку в школу.
В – Я пойду на дискотеку в Огни Уфы.
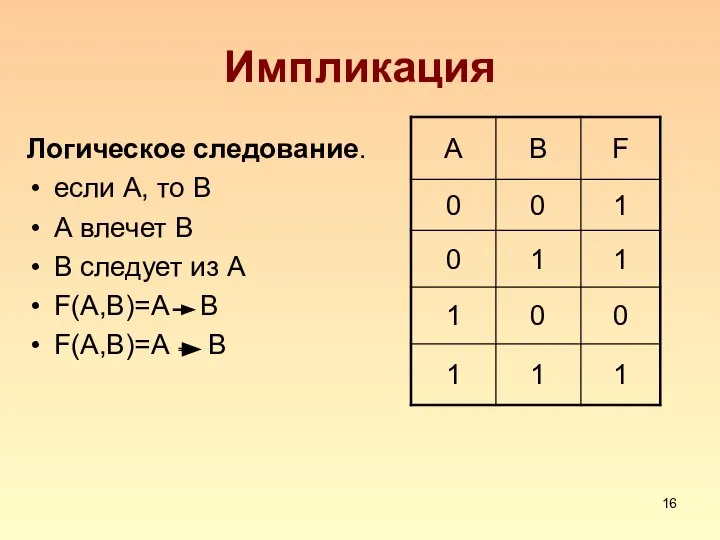
Слайд 16Импликация
Логическое следование.
если А, то В
А влечет В
В следует из А
F(A,B)=А В
F(A,B)=А В
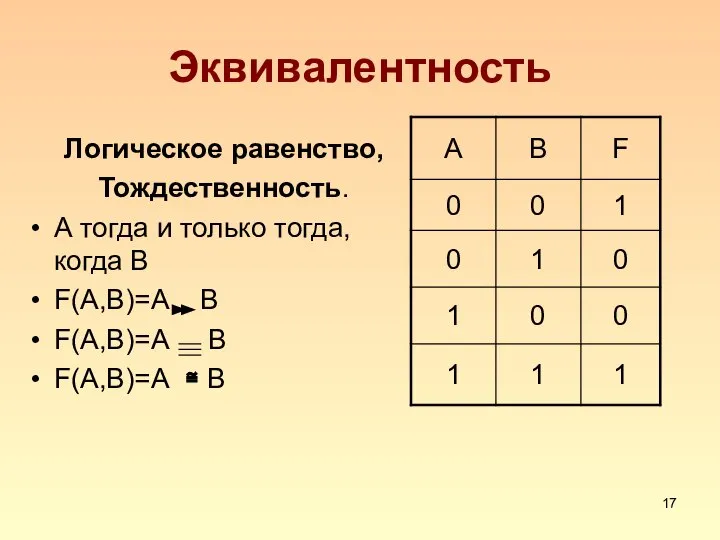
Слайд 17Эквивалентность
Логическое равенство,
Тождественность.
А тогда и только тогда, когда В
F(A,B)=А В
F(A,B)=А В
F(A,B)=А ≅ В
















 Система координат. Графические операторы Basica
Система координат. Графические операторы Basica Шаблон для составления скрипта
Шаблон для составления скрипта ПО для создания интерактивных карт помещений
ПО для создания интерактивных карт помещений История развития вычислительной техники
История развития вычислительной техники Информатика. Введение
Информатика. Введение Копирование формул
Копирование формул Написание литературного обзора
Написание литературного обзора Текстовый процессор MS WORD: работа с таблицами
Текстовый процессор MS WORD: работа с таблицами Объектно-ориентированное программирование. Принципы ООП. Классы, объекты, поля и методы. Уровни доступа
Объектно-ориентированное программирование. Принципы ООП. Классы, объекты, поля и методы. Уровни доступа Rink OS 2019. Версия для разработчиков
Rink OS 2019. Версия для разработчиков Работа с двумерными массивами
Работа с двумерными массивами Разработка плана совершенствования деятельности по управлению ИТ-проектами АО Гознак
Разработка плана совершенствования деятельности по управлению ИТ-проектами АО Гознак Компьютерные технологии и интернет в современном образовании
Компьютерные технологии и интернет в современном образовании Риски, которые надо учитывать при организации обслуживания IT технологий
Риски, которые надо учитывать при организации обслуживания IT технологий Системы счисления
Системы счисления Комплект 3-D моделей пластиковых деталей для автомобилей
Комплект 3-D моделей пластиковых деталей для автомобилей Целевая рассылка Сенлер
Целевая рассылка Сенлер Телемед Бизнес - продукт телемедицинского консультирования
Телемед Бизнес - продукт телемедицинского консультирования Измерение информации. Алфавитный подход к измерению информации
Измерение информации. Алфавитный подход к измерению информации ДУ Информатика 8.12
ДУ Информатика 8.12 Сравнение средств и методов выявления и защиты от фишинговых атак
Сравнение средств и методов выявления и защиты от фишинговых атак Классификация объектов
Классификация объектов АО Концерн Калашниов. 1С:Производственная безопасность. Комплексная
АО Концерн Калашниов. 1С:Производственная безопасность. Комплексная Методические особенности применения модельного конструктора Живая физика (на примере модели Математический маятник)
Методические особенности применения модельного конструктора Живая физика (на примере модели Математический маятник) Анти - вирусы и вирусы
Анти - вирусы и вирусы Создание интернет-ресурса Художественная галерея
Создание интернет-ресурса Художественная галерея Алгоритм обратного распространения ошибки
Алгоритм обратного распространения ошибки Заказ данных спутников серии Landsat с сайта
Заказ данных спутников серии Landsat с сайта