Логика в ЕГЭ

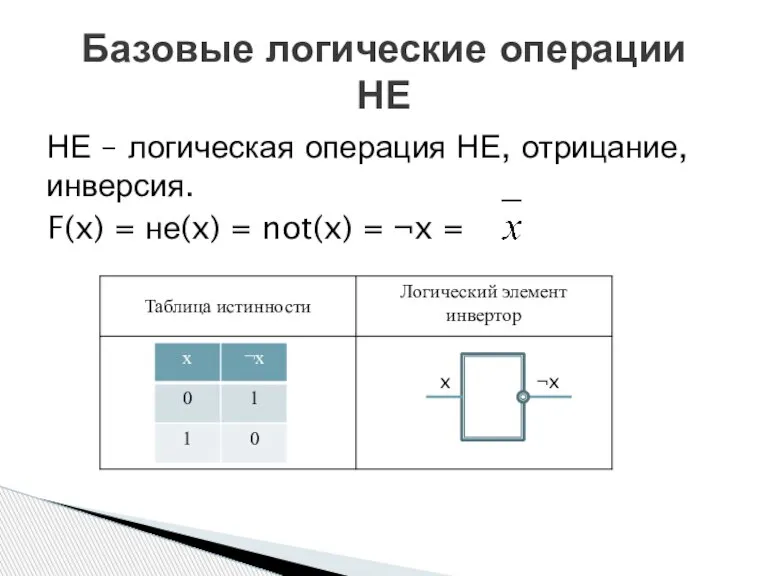
НЕ – логическая операция НЕ, отрицание, инверсия.
F(x) = не(x) = not(x) = ¬x =
Базовые логические операции
НЕ
¬x

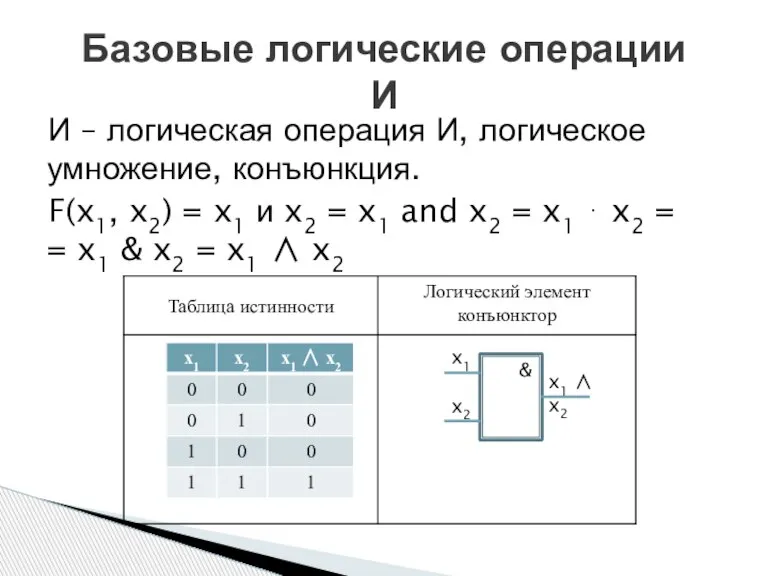
И – логическая операция И, логическое умножение, конъюнкция.
F(x1, x2) = x1 и x2 = x1 and x2 = x1 ⋅ x2 =
= x1 & x2 = x1 ∧ x2
Базовые логические операции
И

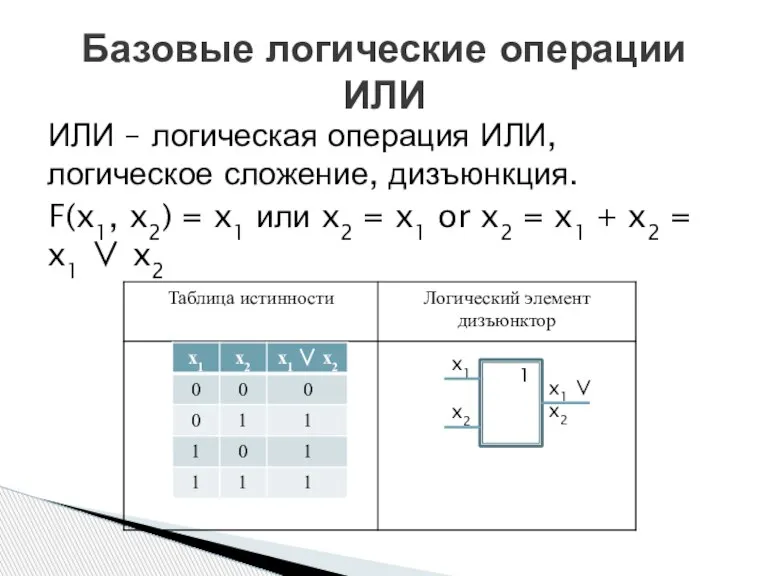
ИЛИ – логическая операция ИЛИ, логическое сложение, дизъюнкция.
F(x1, x2) = x1 или x2 = x1 or x2 = x1 + x2 = x1 ∨ x2
Базовые логические операции
ИЛИ

Аксиомы алгебры логики

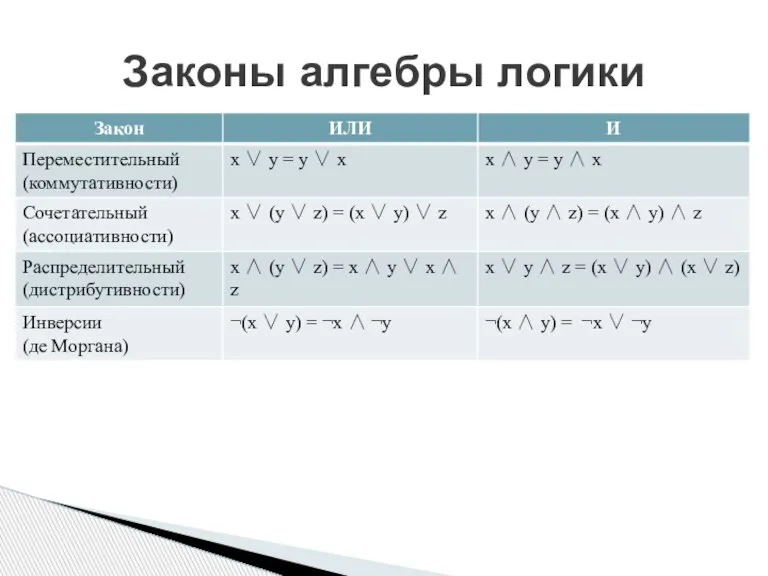
Законы алгебры логики

Операции выполняются слева направо с учетом скобок:
1. Отрицание
2. Конъюнкция
3. Дизъюнкция
4. Исключающее ИЛИ
5. Импликация
6. Эквивалентность
Правила выполнения
логических операций

Решение ЕГЭ №2

Досрочный ЕГЭ 2016 (fipi.ru)

1шаг – минимизация функции.
(x∧y∧¬z) ∨ (x∧y∧z) ∨ (x∧¬y∧¬z)= x∧(y ∨¬z)
1) (x∧y∧¬z) ∨ (x∧y∧z) = x∧y ∧ (¬z∨z) = x∧y
2) x∧y ∨ (x∧¬y∧¬z) = x∧(y ∨ ¬y∧¬z) = x∧((y ∨¬y)∧(y ∨¬z)) =
= x∧(y ∨¬z)
2 шаг – логическая операция И: истина будет тогда, когда все множители истинны.
x = 1 и y ∨ ¬z = 1
По таблице переменная 2 везде = 1 ⇒ x.
Для получения 1 в выражении y ∨ ¬z можно предположить: переменная 1 – y, переменная 3 – z.
0 ∨¬0 = 0∨1 = 1
1 ∨¬0 = 1∨1 = 1
1 ∨¬1 = 1∨0 = 1
Ответ: yxz
Решение

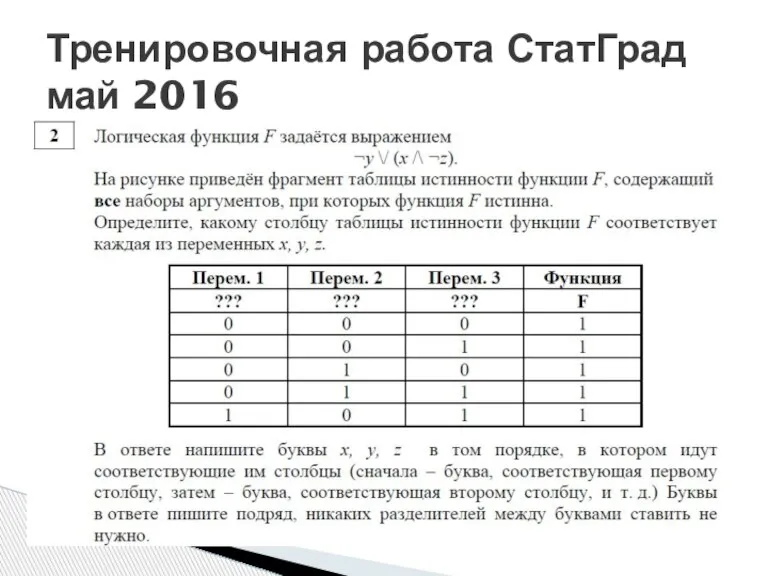
Тренировочная работа СтатГрад май 2016

1шаг – минимизация функции.
¬y ∨ (x∧¬z)= (¬y ∨ x) ∧ (¬y ∨ ¬z) (распределительный закон)
2 шаг – логическая операция И: истина будет тогда, когда все множители истинны.
(¬y ∨ x) =1 и (¬y ∨ ¬z) =1
Подбираем столбцы под первое выражение.
Переменная 1 – y, переменная 3 – х.
¬0 ∨ 0 =1∨0 = 1
¬0 ∨ 1 =1∨1 = 1
¬0 ∨ 0 =1∨0 = 1
¬0 ∨ 1 =1∨1 = 1
¬1 ∨ 1 =0∨1 = 1
Переменная 2 – z. Обязательно сделать проверку на второе уравнение.
Ответ: yzx
Решение

Тренировочная работа СтатГрад ноябрь 2016

1шаг – минимизация функции.
(x∧z) ∨ (x∧¬y∧¬z) = x ∧ (z∨¬y∧¬z) = x ∧ (z∨¬y) ∧ (z∨¬z) = x ∧ (¬y∨z)
2 шаг – логическая операция И: истина будет тогда, когда все множители истинны.
x = 1 и ¬y ∨ z = 1
По таблице переменная 2 везде = 1 ⇒ x.
Для получения 1 в выражении z ∨ ¬y переменная 1 – y, переменная 3 – z.
¬0 ∨ 0 = 1∨0 = 1
¬0 ∨ 1 = 1∨1 = 1
¬1 ∨ 1 = 0∨1 = 1
Ответ: yxz
Решение

Тренировочная работа СтатГрад апрель 2014

1) 1∧0…=0 +
0∧…=0 +
1∧0…=0 –
2) 1∨…=1 –
3) 0∨1…=1 –
4) ¬x6=0 +
0∧…=0 +
Все 1 +
Ответ: 4
Решение
Импликация: 0 будет тогда, когда из 1 следует 0.
И: 1 будет тогда, когда все 1.
ИЛИ: 1 будет тогда, когда хотя бы одна 1.
¬x3=0
x2→x1=0
¬x3=0, а надо 1
Импликация даст 1, а надо 0
x3=1, а надо 0

Тренировочная работа СтатГрад май 2015

х6=0 → F=0 –
? F может быть равно 1 по другим переменным.
¬х4=1 → F=0 –
? F может быть равно 1 по другим переменным.
+
? F может быть равно 0 по другим переменным.
+
¬х4=1 → F=0 –
Ответ: 3
Решение

Демо ЕГЭ 2017

x∧¬y∧(¬z∨w)=1
x=1, ¬y=1, ¬z∨w=1
По таблице: переменная 3 – х, переменная 2 – y. Остаётся определить переменные 1 и 4 по уравнению ¬z∨w=1: переменная 1 – z, переменная 4 – w.
¬0 ∨ 0 = 1
¬0 ∨ 1 = 1
¬1 ∨ 1 = 1
Ответ: zyxw
Решение

Решение ЕГЭ №18

Формулы замены

Досрочный ЕГЭ 2016 (fipi.ru)

1 шаг – минимизация функции.
¬(x∈А) → ((x∈Р) → ¬(x∈Q)) = ¬(x∈А) → (¬(x∈Р) ∨ ¬(x∈Q)) =
= ¬ (¬(x∈А)) ∨ ¬(x∈Р) ∨ ¬(x∈Q)= (x∈А) ∨ ¬(x∈Р) ∨ ¬(x∈Q)
2 шаг – чертёж.
Отрезок P: 1 будет тогда, когда точка не принадлежит отрезку - ¬(x∈Р). То же с Q.
Отрезок А: [30;50].
L = 50-30=20 Ответ: 20
Решение

Тренировочная работа СтатГрад май 2016

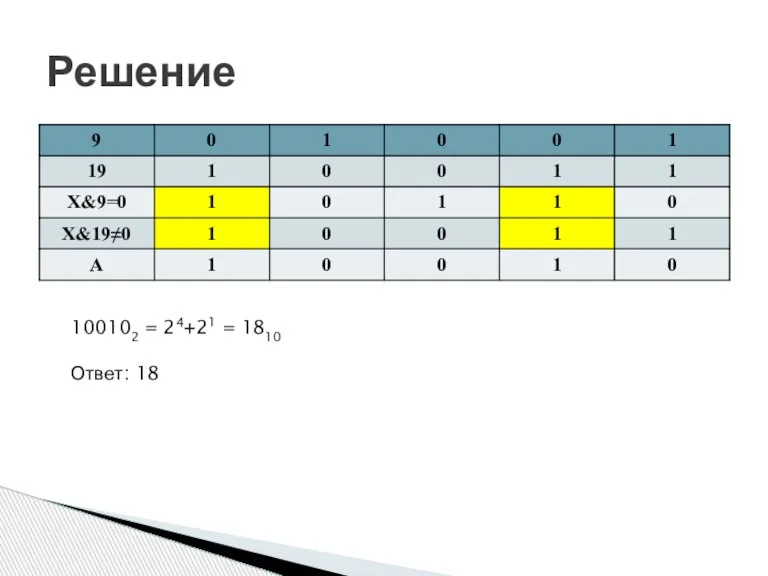
Решение
100102 = 24+21 = 1810
Ответ: 18

Тренировочная работа СтатГрад ноябрь 2016

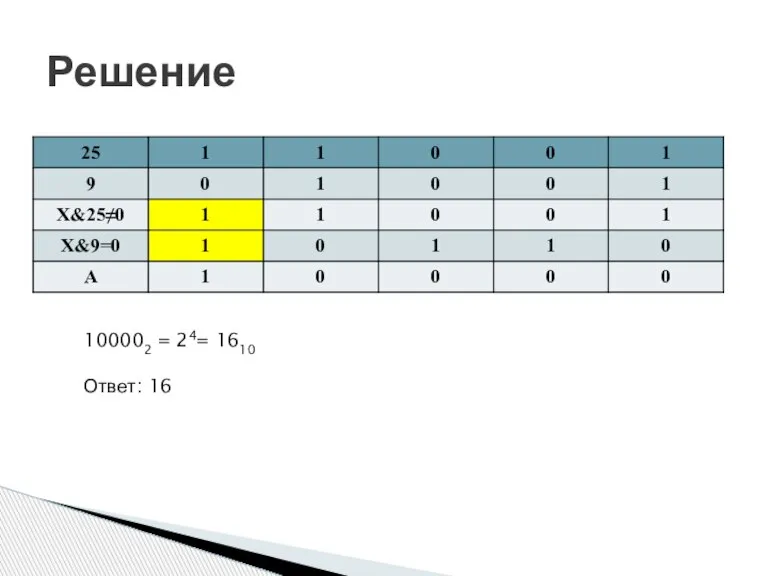
Решение
100002 = 24= 1610
Ответ: 16

Тренировочная работа СтатГрад апрель 2014

1 шаг – минимизация функции.
((x∈P) ∨ (x∈А)) → ((x∈Q) ∨ (x∈A)) = ¬((x∈P) ∨ (x∈А)) ∨ (x∈Q) ∨ (x∈A) = ¬(x∈P) ∧ ¬(x∈А) ∨ (x∈A) ∨ (x∈Q) = (¬(x∈P) ∨ (x∈А)) ∧ (¬(x∈A) ∨ (x∈А)) ∨ (x∈Q) = ¬(x∈P) ∨ (x∈А) ∨ (x∈Q)
2 шаг – чертёж.
Отрезок P: 1 будет тогда, когда точка не принадлежит отрезку - ¬(x∈Р).
Отрезок Q: 1 будет тогда, когда точка принадлежит отрезку.
Отрезок А: [8, 23].
Ответ: 1 ([5,30])
P
Q
8
23
39
58
Решение

Тренировочная работа СтатГрад май 2015

Решение
((x∈А) → (x∈Р)) ∨ (¬(x∈Q) → ¬(x∈А)) =
¬(x∈А) ∨ (x∈Р) ∨ ¬(¬(x∈Q)) ∨ ¬(x∈А) =
¬(x∈А) ∨ (x∈Р) ∨ (x∈Q)
Так как x∉А, диапазон чисел А должен быть объединением множеств P и Q.
Ответ: 18

Демо ЕГЭ 2017

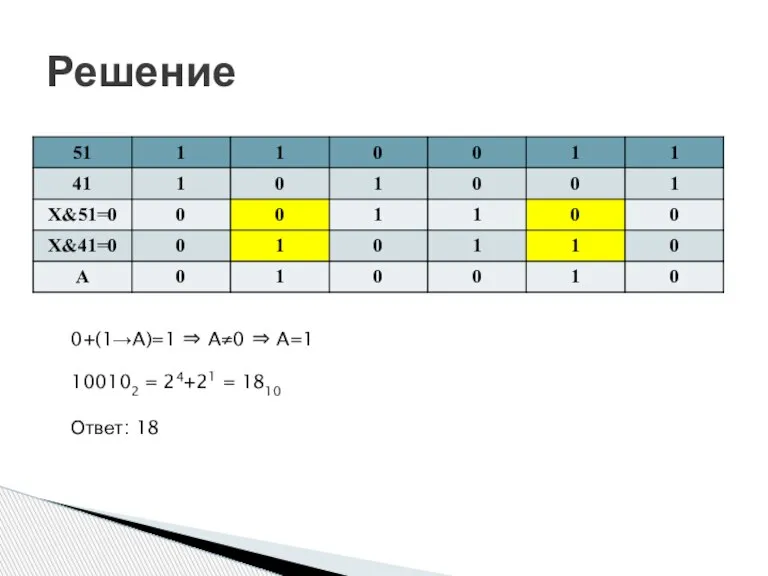
Решение
0+(1→A)=1 ⇒ A≠0 ⇒ A=1
100102 = 24+21 = 1810
Ответ: 18

Решение ЕГЭ №23
Метод отображений

ТР СтатГрад от 26.01.2015

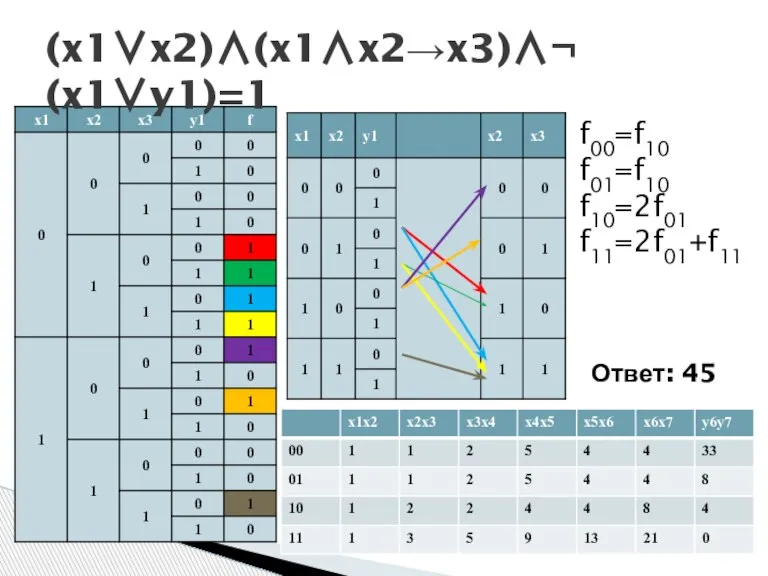
(x1∨x2)∧(x1∧x2→x3)∧¬ (x1∨y1)=1
f00=f10
f01=f10
f10=2f01
f11=2f01+f11
Ответ: 45