Математическая логика (булева алгебра)

Переменные в булевой алгебре
Переменные могут принимать только два значения: 0 и 1.
Результат любых действий над переменными тоже равен или 0, или 1 (число 102 получиться не может).
1 по-другому называют "правдой" или true, 0 – это "ложь", false.
Булева алгебра – основа информатики и программирования. Электронные схемы компьютера работают по правилам булевой алгебры.

Переменные в булевой алгебре
Обычная математика:
A = 13.45
B = -20
А + В = -6.55
А и В могут принимать любые числовые значения, результат – любое число.
Булева алгебра:
А = 0
B = 1
A V B = 1
А и В принимают только значения 0 или 1, результат тоже либо 0, либо 1.

Отрицание (логическое НЕ, ¬, —, !, not)

Конъюнкция (логическое И, ∧, &, and)
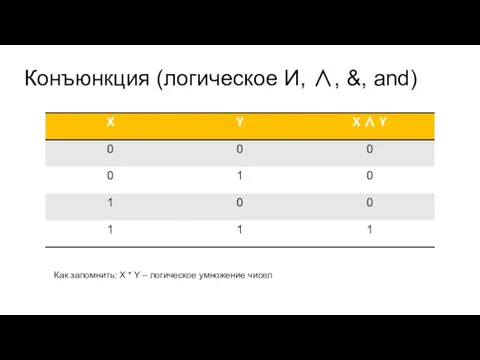
Как запомнить: X * Y – логическое умножение чисел

Дизъюнкция (логическое ИЛИ, ∨, |, or)
Как запомнить: X + Y – логическое сложение чисел

Импликация (следование, →)
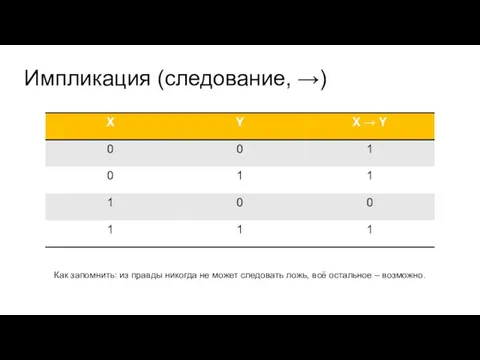
Как запомнить: из правды никогда не может следовать ложь, всё остальное – возможно.

Эквивалентность (↔, ≡)

Упрощение логических выражений

Приоритет логических операций
Как и в обычной математике, на основе операций ¬, ∧, ∨, →, ↔ составляются длинные формулы.
Пример:
F(A, B, C, D) = A ˄ B ↔ C → D
Действия в выражении выполняются в соответствии с приоритетом операций:
1) выражение в скобках – высший приоритет;
2) отрицание (¬);
3) конъюнкция (∧);
4) дизъюнкция (∨);
5) импликация (→);
6) эквиваленция (↔) – нисший приоритет.