Математическая логика в задании 18 (ЕГЭ)

Основные понятия математической логики в задании №18
&
Дел
>, <, =
Введение

Дизъюнкция
Отрицание
Конъюнкция
Алгоритм решения
Введение
&
Дел
>, <, =
Записать исследуемое выражение в привычных условных обозначениях.
Упростить выражение (Не ЛОЖЬ = ИСТИНА)

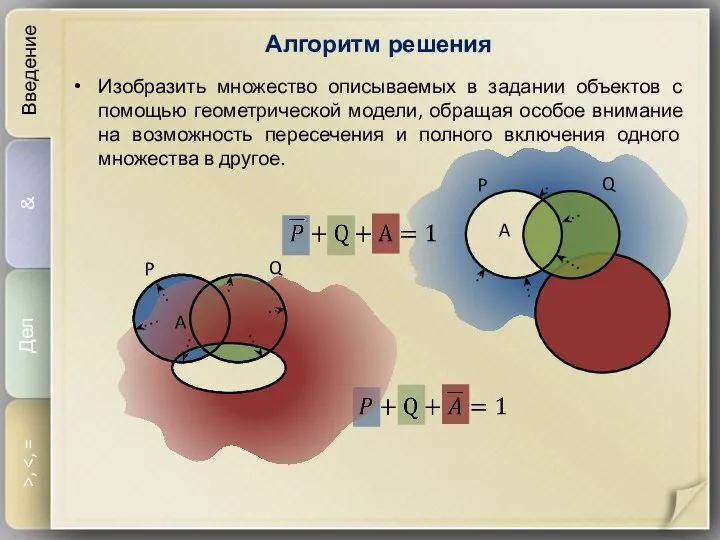
Алгоритм решения
Введение
&
Дел
>, <, =
Изобразить множество описываемых в задании объектов с помощью геометрической модели, обращая особое внимание на возможность пересечения и полного включения одного множества в другое.
P
Q
P
Q
A
A

Алгоритм решения
Введение
&
Дел
>, <, =
Найти «скрытые» составные высказывания. Записать, используя логические операции через простые.
В двоичном представлении числа x есть единица в четвертом разряде.
В двоичном представлении числа x есть хотя бы одна единица, совпадающая с единицами числа 6.
ДЕЛ(x, 2)
Число x кратно 2
ДЕЛ(x, 4)
Число x кратно 4

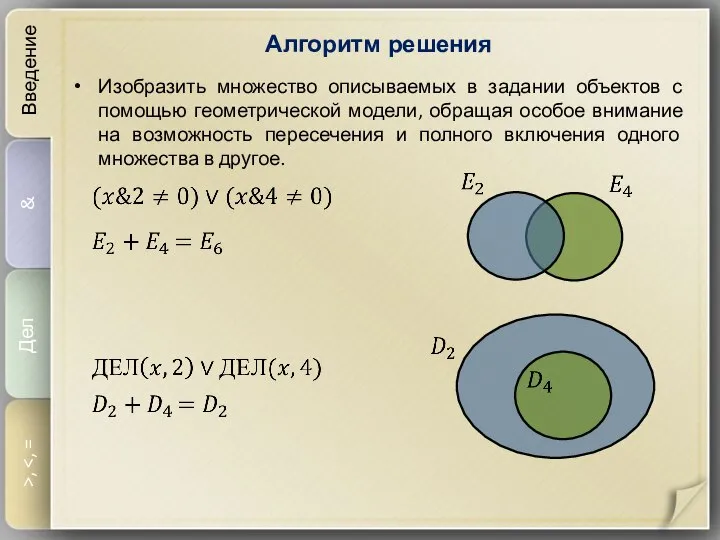
Алгоритм решения
Введение
&
Дел
>, <, =
Изобразить множество описываемых в задании объектов с помощью геометрической модели, обращая особое внимание на возможность пересечения и полного включения одного множества в другое.

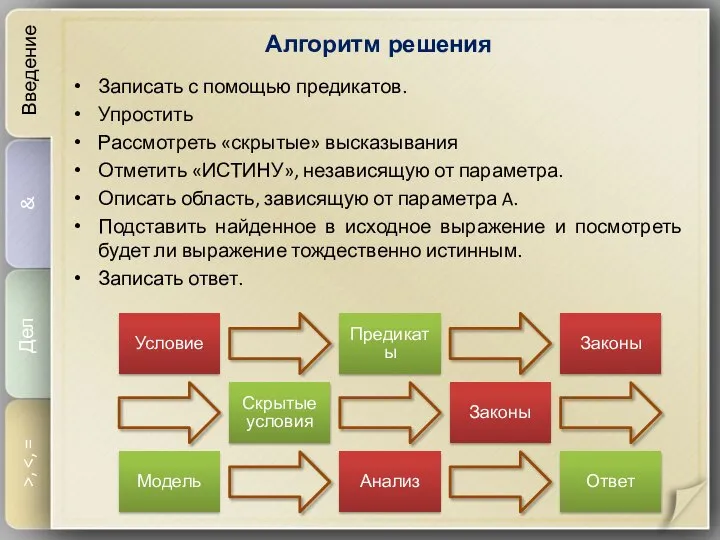
Алгоритм решения
Введение
&
Дел
>, <, =
Записать с помощью предикатов.
Упростить
Рассмотреть «скрытые» высказывания
Отметить «ИСТИНУ», независящую от параметра.
Описать область, зависящую от параметра A.
Подставить найденное в исходное выражение и посмотреть будет ли выражение тождественно истинным.
Записать ответ.
Условие
Предикаты
Законы
Скрытые условия
Законы
Модель
Анализ
Ответ

Задание с битовыми операциями
Введение
&
Дел
>, <, =
Ответ: 32, 16, 2
, 50
, 18, 34, 48

Задание с битовыми операциями
Введение
&
Дел
>, <, =
Ответ: 45

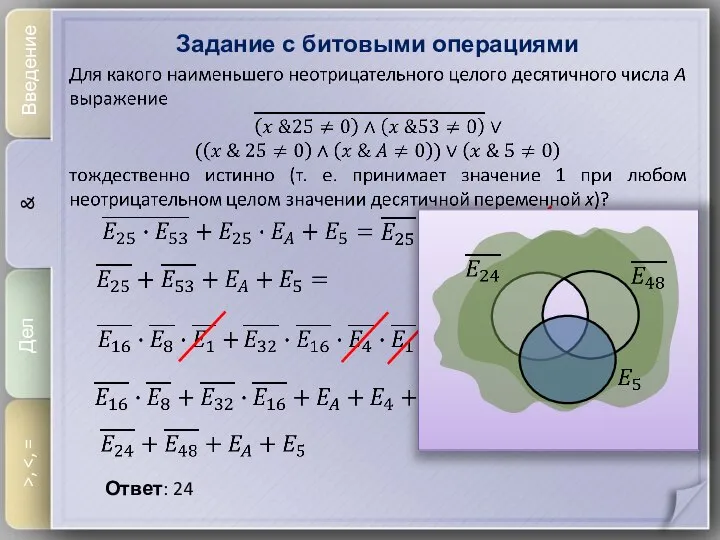
Задание с битовыми операциями
Введение
&
Дел
>, <, =
Ответ: 24

Задания на делимость
Введение
&
Дел
>, <, =
Если число делится на каждое из взаимно простых чисел, то оно делится и на их произведение.
Если число делится на произведение взаимно простых чисел, то оно делится и на каждое из них.

Задания на делимость
Введение
&
Дел
>, <, =
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
(ДЕЛ(x, 15) ∧ ¬ДЕЛ(x, 21)) → (¬ДЕЛ(x, A) ∨ ¬ДЕЛ(x, 15))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 7

Задания на делимость
Введение
&
Дел
>, <, =
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наибольшего натурального числа А формула
(ДЕЛ(x, 40) ∨ ДЕЛ(x, 32)) → ДЕЛ(x, A)
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 8

Задания на делимость
Введение
&
Дел
>, <, =
Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
ДЕЛ(x, 2520) ∨ ¬ДЕЛ(x, 5940) ∨ (¬ДЕЛ(x, A)
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 56

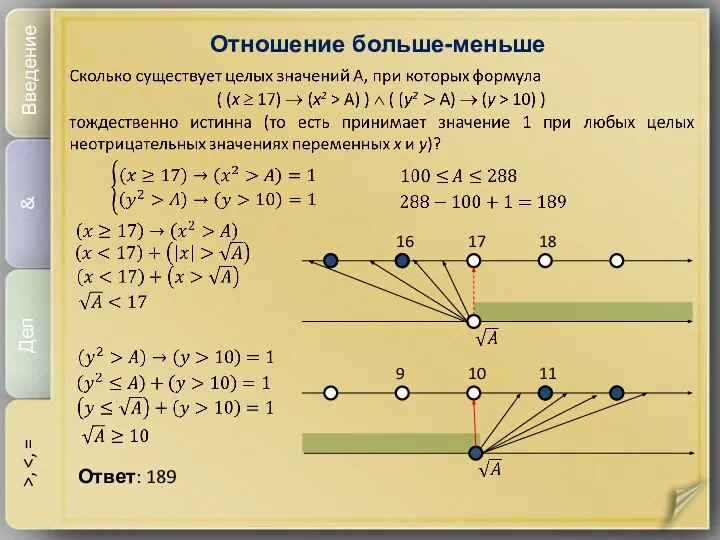
Отношение больше-меньше
Введение
&
Дел
>, <, =
Ответ: 189