Содержание
- 2. МЕТОДЫ И МОДЕЛИ ОЦЕНКИ КОЛИЧЕСТВА ИНФОРМАЦИИ способы измерения информации: объемный, энтропийный, алгоритмический.
- 3. Объемный метод измерения информации Объемный является самым простым и грубым способом измерения информации. Соответствующую количественную оценку
- 4. Энтропийный подход к измерению информации Получатель информации (сообщения) имеет определенные представления о возможных наступлениях некоторых событий.
- 5. Алгоритмический метод оценки информации Любому сообщению можно приписать количественную характеристику, отражающую сложность (размер) программы, которая позволяет
- 6. Для обработки данных с помощью средств вычислительной техники они должны быть преобразованы в понятную для ЭВМ
- 7. ФОРМЫ ПРЕДСТАВЛЕНИЯ И ПРЕОБРАЗОВАНИЯ ИНФОРМАЦИИ Формирование представления информации называется ее кодированием. В более узком смысле под
- 8. При кодировании информации ставятся следующие цели: 1) удобство физической реализации; 2) удобство восприятия; 3) высокая скорость
- 9. В отличие от обычной словесной формы, принятой в письменной речи, информация в памяти ЭВМ записывается в
- 10. Для автоматизации работы с данными унифицируют форму представления данных – применяют кодирование Кодирование- выражение данных одного
- 11. В более узком смысле под кодированием понимается переход от исходного представления информации, удобного для восприятия человеком,
- 12. При кодировании информации ставятся следующие цели: 1) удобство физической реализации; 2) удобство восприятия; 3) высокая скорость
- 13. Кодирование данных двоичным кодом Двоичное кодирование- представление данных последовательностью двух знаков : 0 и 1. Двоичные
- 14. В качестве эталона меры измерения информации выбран абстрактный объект, который может находиться в одном из 2-х
- 15. Единицы измерения данных 1Мбайт = 1024 Кбайт = 210 байт 1Гбайт = 1024 Мбайт = 230
- 16. Кодирование данных двоичным кодом 00 01 10 11 000 001 010 011 100 101 110 111
- 17. СИСТЕМЫ СЧИСЛЕНИЯ Системой счисления называется совокупность приемов наименования и записи чисел. В любой системе счисления для
- 18. ПОЗИЦИОННЫЕ СИСТЕМЫ СЧИСЛЕНИЯ Система счисления называется позиционной, если значение каждой цифры (ее вес) изменяется в зависимости
- 19. Десятичная позиционная система счисления основана на том, что десять единиц каждого разряда объединяются в одну единицу
- 20. Число К единиц какого-либо разряда, объединяемых в единицу более старшего разряда, называют основанием позиционной системы счисления,
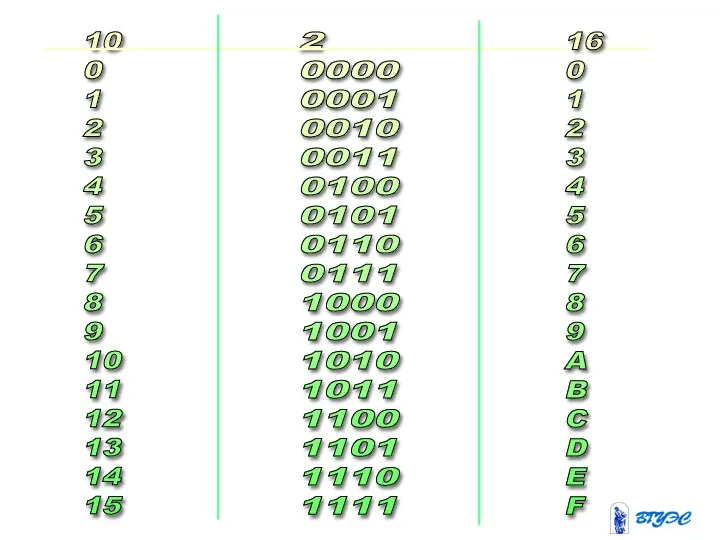
- 21. Системы счисления: 10 (десячичная): 0,1,2,3,4,5....9 2 (двочная): 0,1 16 (шеснадцатиричная): 0...9ABCDEF
- 22. 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
- 23. Правила перевода из одной системы счисления в другую
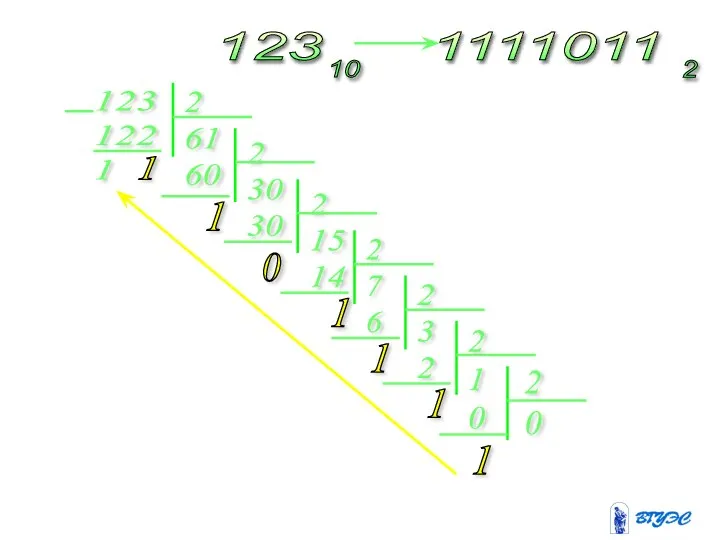
- 24. 1) Из 10 в 2 Исходное число в 10 С/С подвергается делению на основание той С/С,
- 25. 123 122 1 2 61 60 2 30 30 2 15 14 2 7 6 2
- 26. 123 112 11 16 7 0 7 16 0 11 7 123 7B 10 16
- 27. 2) 2, 16 в 10 Исходное число раскрывается как сумма n *-ий соответсвующих цифр исходного числа
- 28. 1111011 = 1*2 +1*2 +1*2 +1*2 +0*2 +1*2 +1*2 = 123 2 10 5 6 4
- 29. 3) 2 в 16 и 16 в 2 При переводе 2 в 16 исходное число делится
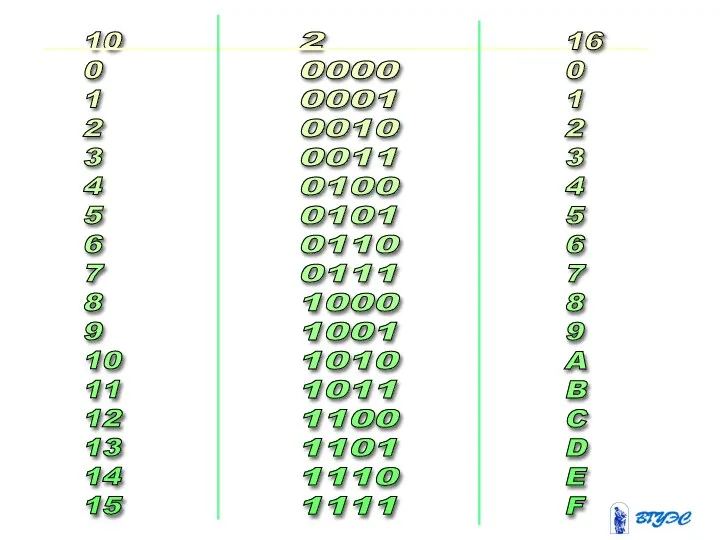
- 30. 10 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
- 31. 7B =01111011 0001 1011 1011 = 1BB 1 B B 16 2 2 16
- 32. Арифметические действия над числами в любой позиционной системе счисления производятся по тем же правилам, что и
- 33. ДВОИЧНАЯ АРИФМЕТИКА
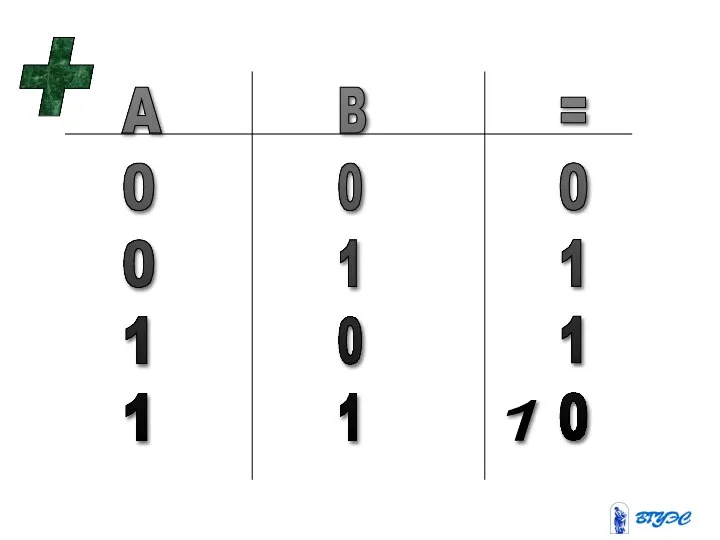
- 34. + A 0 0 1 1 B 0 1 0 1 = 0 1 1 0
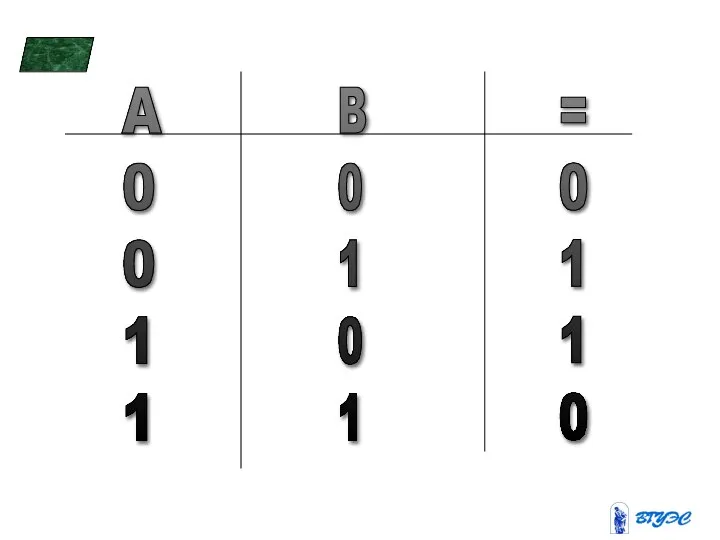
- 35. - A 0 0 1 1 B 0 1 0 1 = 0 1 1 0
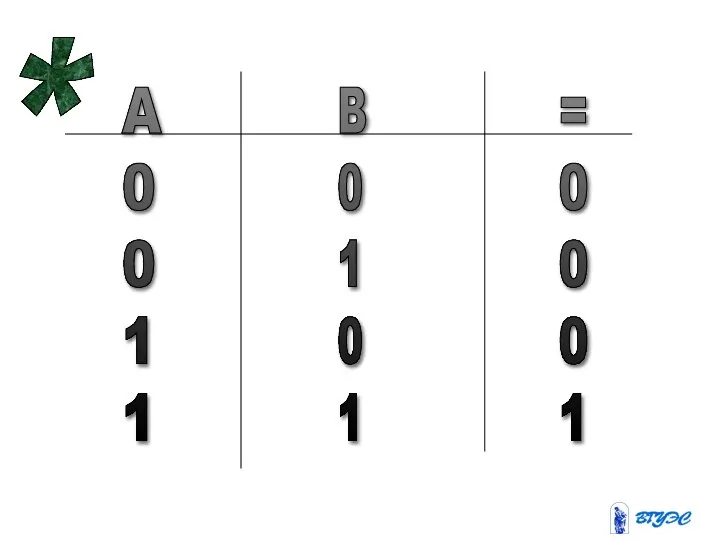
- 36. * A 0 0 1 1 B 0 1 0 1 = 0 0 0 1
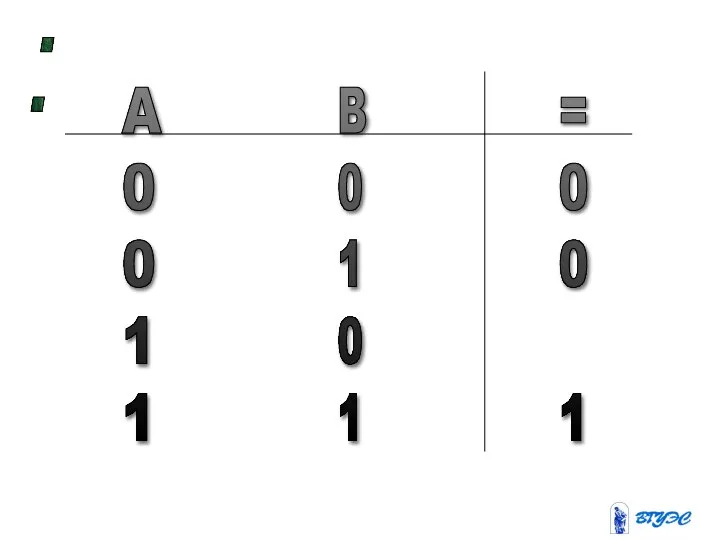
- 37. A 0 0 1 1 B 0 1 0 1 = 0 0 1 :
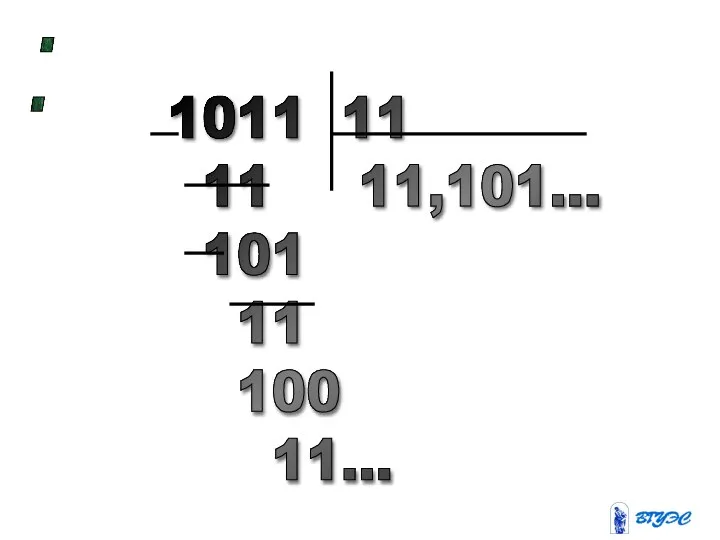
- 38. : 1011 11 11 11,101... 101 11 100 11...
- 39. Кодирование целых чисел: От 0 до 255 - 8 бит от 0 до 65535 - 16
- 40. Для кодирования действительных чисел используют 80-разрядное кодирование.
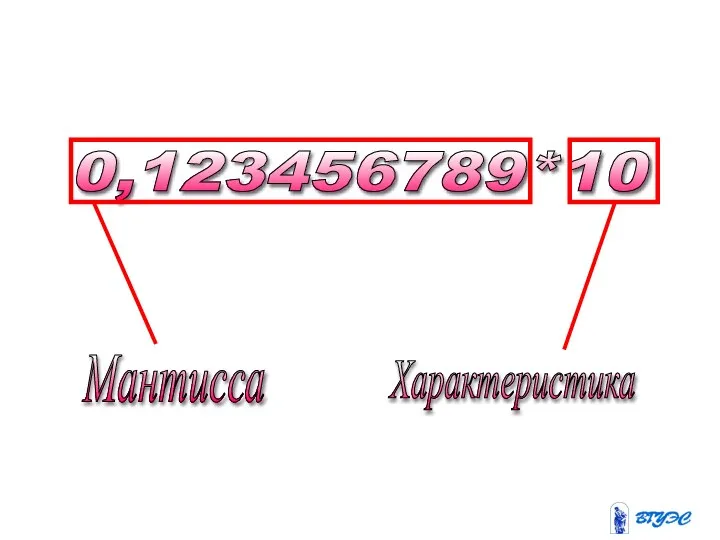
- 41. При этом число предварительно преобразуется в НОРМАЛИЗОВАННУЮ ФОРМУ: 3,1415926 = 0,31415926*10 300000 = 0,3*10 123456789 =
- 42. 0,123456789*10 Мантисса Характеристика
- 43. Кодирование текстовых данных Двоичных код используют при кодировании текста, когда каждому символу алфавита сопоставляется определенное число.
- 44. Кодирование текстовых данных: При кодировании текстовой информации каждому символу соответствует определенный код 1 буква - 8
- 45. UNICODE - универсальная система кодирования, основанная на 16-разрядном кодировании символов, позволяющих обеспечить уникальные коды для 65
- 46. Кодирование графических данных: Для кодирования графических данных применяется принцип декомпозиции; производные цвета зеленый, красный, синий (RGB)
- 47. Кодирование звуковых данных: Метод FM Метод Wave-Table
- 49. Скачать презентацию
























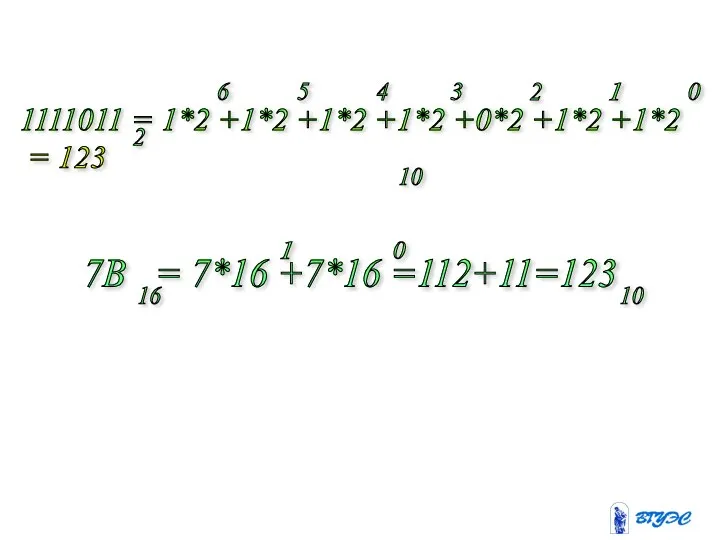

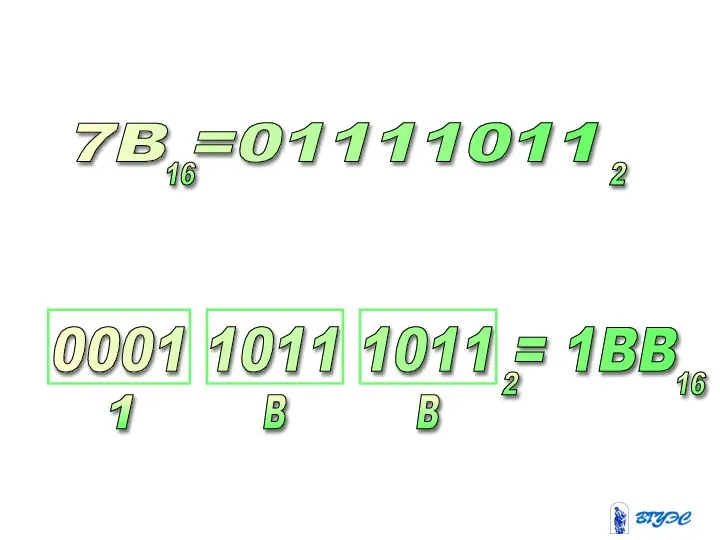









 Существенные свойства и принятия
Существенные свойства и принятия Найди и удали понятия, не связанные с информатикой
Найди и удали понятия, не связанные с информатикой Представление чисел в компьютере. Математические основы информатики
Представление чисел в компьютере. Математические основы информатики Изменения в электронном комплекте аттестационных документов
Изменения в электронном комплекте аттестационных документов Операционные системы, среды и оболочки
Операционные системы, среды и оболочки Windows 11 – операционная система 2021
Windows 11 – операционная система 2021 Введение в Processing
Введение в Processing Оценка качества автоматизации
Оценка качества автоматизации Запросы в СУБД
Запросы в СУБД Презентация на тему Основные понятия программы PowerPoint
Презентация на тему Основные понятия программы PowerPoint  Исполняемые тэги. Псевдоклассы
Исполняемые тэги. Псевдоклассы Готовность к внедрению автоматизированной системы мониторинга движения лекарственных
Готовность к внедрению автоматизированной системы мониторинга движения лекарственных Как работать с 1с не в локальной сети
Как работать с 1с не в локальной сети Работа с памятью
Работа с памятью Обработка персональных данных. Семинар-задание
Обработка персональных данных. Семинар-задание Логические операции
Логические операции Мастер-класс по информатике. Где нас ждут?
Мастер-класс по информатике. Где нас ждут? Уменьшение веса технологических машин, деталей и оборудования посредством трехмерного моделирования
Уменьшение веса технологических машин, деталей и оборудования посредством трехмерного моделирования Компьютерные системы счисления
Компьютерные системы счисления Актуальные data-опции для корпоративных клиентов
Актуальные data-опции для корпоративных клиентов Содержательный подход к измерению информации
Содержательный подход к измерению информации Визуализация информации в текстовых документах
Визуализация информации в текстовых документах 7 ключевых навыков интернет-помощника
7 ключевых навыков интернет-помощника История развития Dassault Systèmes
История развития Dassault Systèmes Особенности современных интернеткоммуникаций
Особенности современных интернеткоммуникаций Форматирование, стили, оглавление
Форматирование, стили, оглавление Компьютерные вирусы
Компьютерные вирусы Фрактальная графика. Моделирование рельефа горной гряды с помощью фрактальных методов
Фрактальная графика. Моделирование рельефа горной гряды с помощью фрактальных методов