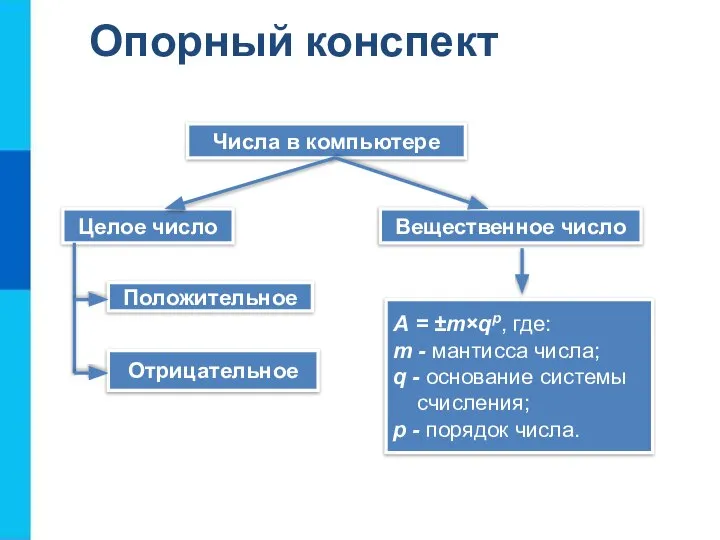
целое число можно рассматривать как вещественное, но с нулевой дробной частью.
Обоснуйте целесообразность наличия особых способов компьютерного представления целых чисел.
Представьте число 6310 в беззнаковом 8-разрядном формате.
Найдите десятичные эквиваленты чисел по их прямым кодам, записанным в 8-разрядном формате со знаком:
а) 01001100;
б) 00010101.
Какие из чисел 4438, 1010102, 25610 можно сохранить в 8-разрядном формате?
Запишите следующие числа в естественной форме:
а) 0,3800456 · 102;
б) 0,245 · 10–3;
в) 1,256900Е+5;
г) 9,569120Е–3.
Запишите число 2010,010210 пятью различными способами в нормальной форме.
Запишите следующие числа в нормальной форме с нормализованной мантиссой - правильной дробью, имеющей после запятой цифру, отличную от нуля:
а) 217,93410;
б) 7532110;
в) 0,0010110.







 Call method with value types arguments
Call method with value types arguments Интернет – телевидение (IPTV)
Интернет – телевидение (IPTV) Школа “Успех в Internet PRO100”
Школа “Успех в Internet PRO100” Дистанционное обучение. Предаттестационная подготовка
Дистанционное обучение. Предаттестационная подготовка Презентация на тему Информация и знания
Презентация на тему Информация и знания  Парадигмы объектно-ориентированного программирования
Парадигмы объектно-ориентированного программирования Интеллектуальные информационные системы наукоемких производств
Интеллектуальные информационные системы наукоемких производств Табличный процессор Microsoft Excel
Табличный процессор Microsoft Excel Графические информационные модели. Моделирование и формализация
Графические информационные модели. Моделирование и формализация информатика Художиткова
информатика Художиткова Программирование на языке Python
Программирование на языке Python Как бизнес-знакомства помогают организатору
Как бизнес-знакомства помогают организатору Язык Basic. Технология разработки программного обеспечения
Язык Basic. Технология разработки программного обеспечения Инвентаризация ОС по шагам
Инвентаризация ОС по шагам Алгоритм. Циклический алгоритм. While, for. Range. Random
Алгоритм. Циклический алгоритм. While, for. Range. Random Облачные технологии
Облачные технологии Возможности текстового процессора Word
Возможности текстового процессора Word Язык программирования Pascal
Язык программирования Pascal Основные понятия баз данных
Основные понятия баз данных Організаційно-правові засади захисту інформації
Організаційно-правові засади захисту інформації Разработка сайта, который станет удобным сервисом для обмена сообщениями заказчиков и исполнителей
Разработка сайта, который станет удобным сервисом для обмена сообщениями заказчиков и исполнителей Оптические кабели
Оптические кабели Информация и информационные процессы. Тест
Информация и информационные процессы. Тест Алгоритм ввода ассортимента селлеров в Ozon Express
Алгоритм ввода ассортимента селлеров в Ozon Express Организация документооборота. Информационно-поисковые справочники в системе НСА АФ РФ
Организация документооборота. Информационно-поисковые справочники в системе НСА АФ РФ Графический интерфейс Windows
Графический интерфейс Windows Создание текста в документе Microsoft Word. Урок 3
Создание текста в документе Microsoft Word. Урок 3 Тема 2_2 Лекция 5 Хранение информации
Тема 2_2 Лекция 5 Хранение информации