Матем.схемы сети Петри

1 Особенности сетей Петри и области их применения
Теория сетей Петри зародилась в 1962 году.
Сети Петри разрабатывались специально для моделирования тех систем, которые содержат взаимодействующие параллельные компоненты. Впервые сети Петри предложил Карл Адам Петри. В своей докторской диссертации "Kommunikation mit Automaten" ("Связь автоматов") Петри сформулировал основные понятия теории связи асинхронных компонент вычислительной системы. В частности, он подробно рассмотрел описание причинных связей между событиями. Его диссертация посвящена главным образом теоретической разработке основных понятий, с которых начали развитие сети Петри.

Работа Петри привлекла внимание сотрудников из проекта Information System Theory (Теория информационных систем) фирмы Applied Data Research (ADR). Ими была развита большая часть начал теории, предложены обозначения и представления сетей Петри; показали, как сети Петри можно применить к анализу и моделированию систем, включающих параллельные компоненты.
В настоящее время сети Петри являются распространенной моделью, позволяющей описывать структуру и взаимодействие параллельно действующих объектов и процессов.
Достоинства аппарата сетей Петри:
1) Сети Петри позволяют моделировать асинхронность и недетерминизм параллельных, независимых событий, параллелизм конвейерного типа, конфликтные ситуации между процессами.

2) Сети Петри позволяют описывать как типовые ситуации в дискретных подсистемах, так и общую динамику работы сложной асинхронной системы.
3) Сети Петри позволяют производить иерархическую детализацию программных и аппаратных подсистем модели, производить совместное отображение структуры управления и потоков данных.
4) В последние годы появился ряда классов сетей, ориентированных на моделирование сложных систем с учетом таких факторов, как приоритетность процессов (сети с проверкой на нуль, приоритетные сети), временные параметры событий (сети Мерлина, временные сети), совместного отображения структуры управления и потоков данных (Е-сети).

2 Основные определения. Способы задания сетей Петри
Сеть Петри – это двудольный ориентированный мультиграф, все множество X вершин которого разбито на два класса так, что дуги соединяют вершины только из разных классов.
Эти классы вершин образуются:
множеством позиций обозначаются кружочками O
множеством переходов обозначаются планками —

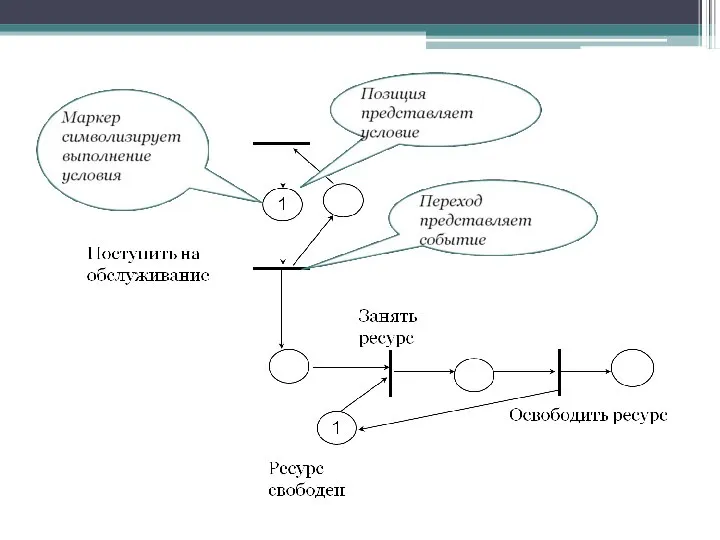
При моделировании отражаются два аспекта систем: события и условия.
Возможность наступления событий обеспечивается выполнением определенных условий.
Условиям соответствуют позиции сети Петри, а событиям, происходящим в системе, соответствуют переходы.
Для представления динамики функционирования позициям могут присваиваться фишки, которые изображаются точками внутри вершин-позиций.
Присвоение фишек позициям сети Петри называется маркировкой, или разметкой.
Сети Петри функционируют, переходя от одной маркировки к другой.

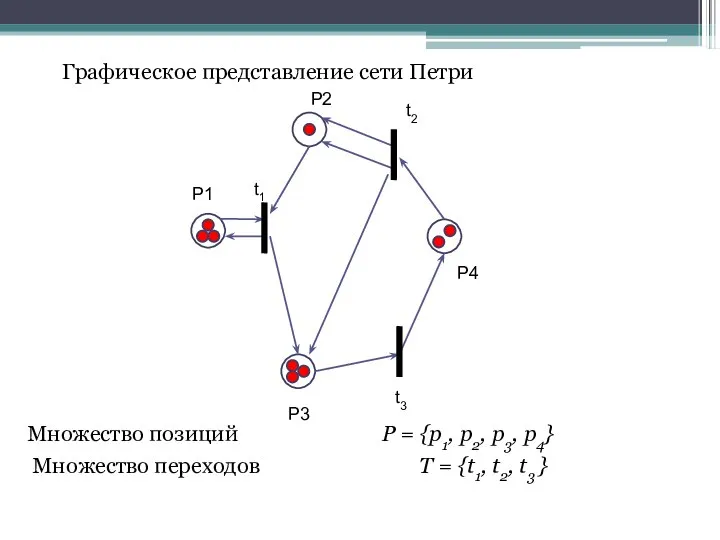
Графическое представление сети Петри
Множество позиций P = {p1, p2, p3, p4}
Множество переходов T = {t1, t2, t3 }
P1
P2
P3
P4
t1
t2
t3

Начальная маркировка сети обозначается вектором
- определяют для каждой позиции pi количество фишек в этой позиции.
Начальная маркировка сети μ0 = [3 1 3 2].
Как и любой граф, сеть Петри может быть задана графическим, аналитическим и матричным способами.
При аналитическом способе сеть Петри задается как C = (P,T,F,H,μ0), где, кроме множеств позиций Р и переходов Т, задаются входная F и выходная Н функции.
Через F(tj) обозначается множество входных позиций, а через H(tj) – множество выходных позиций перехода tj; μ0 – начальная маркировка сети.

F(t1) = {p1, p2}, H(t1) = {p1, p3 },
F(t2) = {p4}, H(t2) = {p2, p2, p3},
F(t3) = {p3}, H(t3) = {p4 }.
μ0 [3 1 3 2]
Матричная форма определения сети Петри эквивалентна аналитическому способу задания C = (P,T,D–,D+,μ0). Здесь D– и D+ – матрицы входных и выходных инциденций соответственно размером m × n, где m – число переходов и n – число позиций.
Элемент dij– матрицы D– равен кратности дуг, входящих в i-й переход из j-й позиции.
Элемент dij+ матрицы D+ равен кратности дуг, выходящих из i-ro перехода в j-ю позицию.

Для рассматриваемой сети Петри
Матрица D = D+ – D - - матрица инцидентности сети Петри

3 Функционирование сетей Петри
Выполнение определенных условий связано с появлением меток в соответствующих этим условиям позициях.
Последовательность событий, происходящих в моделируемой системе, отображается срабатыванием переходов.
В результате срабатывания одного из переходов сети происходит перераспределение фишек между позициями, и маркировка сети изменяется.
Сеть Петри функционирует, переходя от одной маркировки к другой.

Необходимое условие срабатывания перехода ti:
Каждая из его входных позиций должна иметь не меньше фишек, чем число дуг из этой позиции в переход, т. е.
Переход ti, для которого выполняется данное условие, называется разрешенным.
В результате срабатывания перехода ti из всякой входной позиции pj перехода ti удаляется столько фишек, сколько дуг ведет из pj в ti, а в каждую выходную позицию pk помещается столько фишек, сколько дуг ведет из ti в pk.
Переходы ti могут срабатывать в любом порядке, возникающий порядок появления событий не однозначен. Разрешенные переходы не влияют друг на друга.

P1
P2
P3
P4
t1
t2
t3
P1
P2
P3
P4
t1
t2
t3

P1
P2
P3
P4
t1
t2
t3
P1
P2
P3
P4
t1
t2
t3

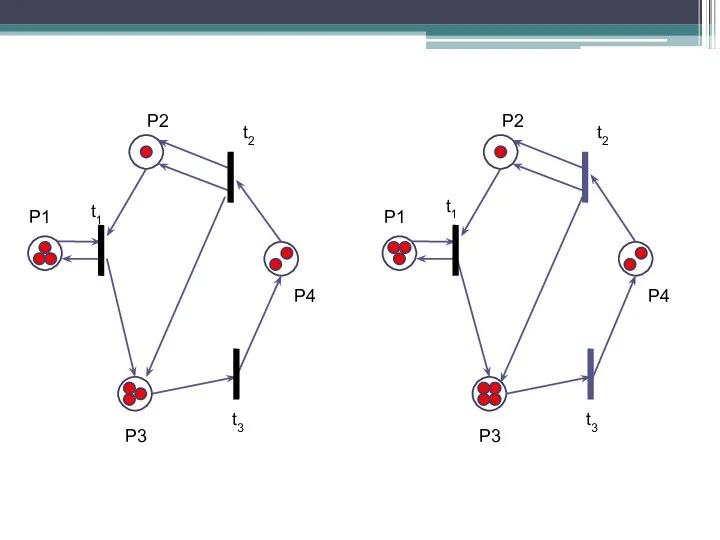
При начальной маркировке μ0 =[3 1 3 2] сети Петри разрешенными являются все переходы t1, t2, и t3.
Условие срабатывания перехода t1 в имеющейся маркировке μ записывается следующим образом:
где eT[i] – вектор-строка, компоненты которого соответствуют переходам и все равны нулю, за исключением i-й, которая равна единице.
Срабатывание перехода рассматривается как мгновенное событие, занимающее нулевое время.
Проверим условие срабатывания перехода t1, t2, и t3.

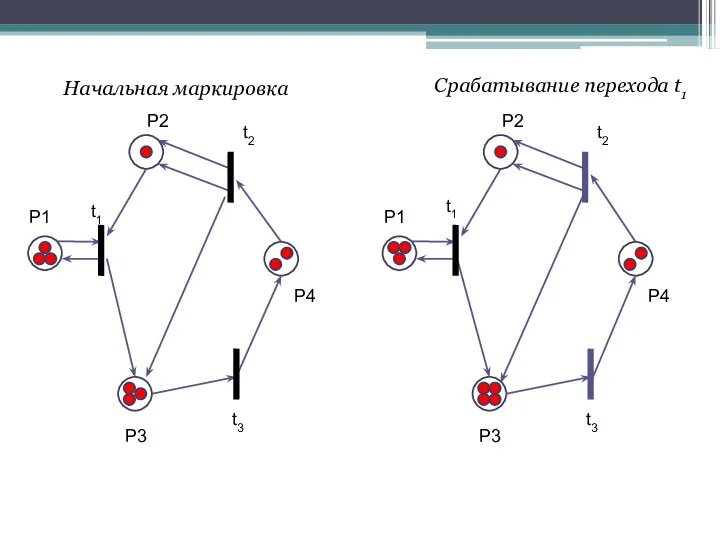
Переход t1
[μ0] ≥ [100]* D– = [100] ·
[3 1 3 2] ≥ [1100] – условие выполняется, переход разрешен.
Векторы сравниваются по каждой из составляющих.
В результате срабатывания ti возникает новая маркировка

P1
P2
P3
P4
t1
t2
t3
P1
P2
P3
P4
t1
t2
t3
Начальная маркировка
Срабатывание перехода t1

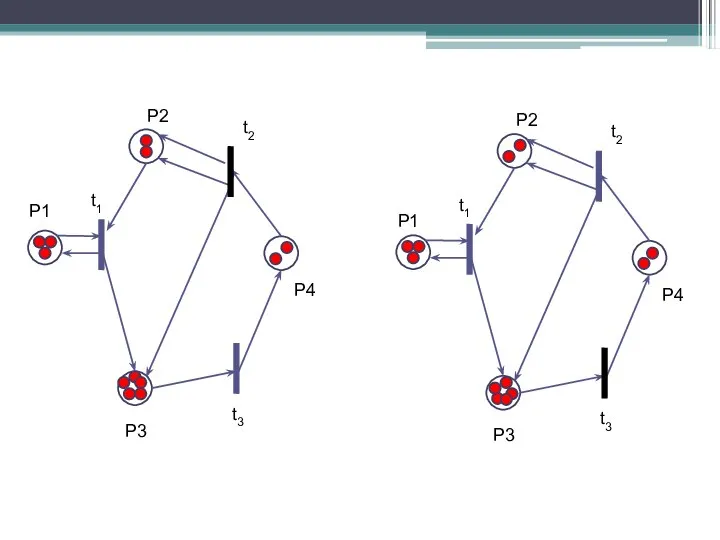
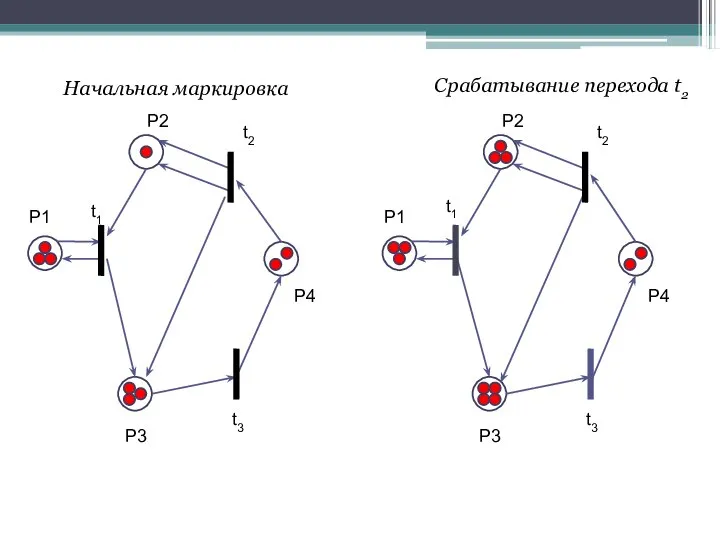
Переход t2
[μ0] ≥ [010]* D– = [010] ·
[3132] ≥ [0001] – условие выполняется, переход разрешен.
Новая маркировка при срабатывании перехода t2 равна:

P1
P2
P3
P4
t1
t2
t3
P1
P2
P3
P4
t1
t2
t3
Начальная маркировка
Срабатывание перехода t2

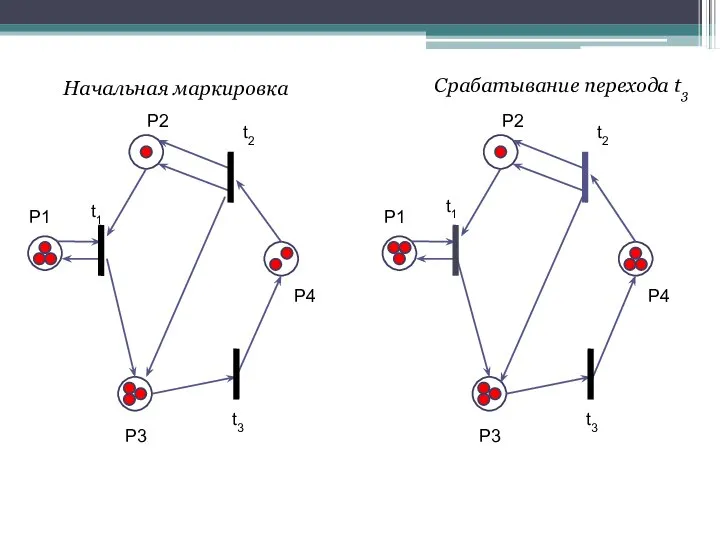
Переход t3
[μ0] ≥ [001]* D– = [001] ·
[3132] ≥ [0010] – условие выполняется, переход разрешен.
Новая маркировка при срабатывании перехода t3 равна:

P1
P2
P3
P4
t1
t2
t3
P1
P2
P3
P4
t1
t2
t3
Начальная маркировка
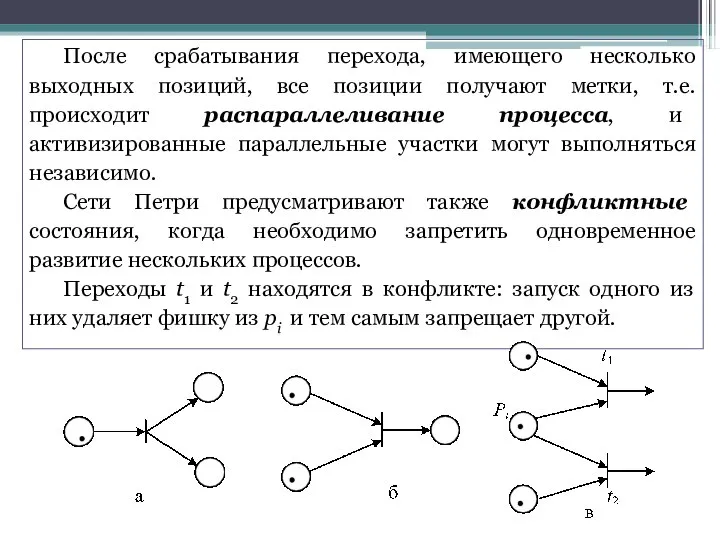
Срабатывание перехода t3

После срабатывания перехода, имеющего несколько выходных позиций, все позиции получают метки, т.e. происходит распараллеливание процесса, и активизированные параллельные участки могут выполняться независимо.
Сети Петри предусматривают также конфликтные состояния, когда необходимо запретить одновременное развитие нескольких процессов.
Переходы t1 и t2 находятся в конфликте: запуск одного из них удаляет фишку из pi и тем самым запрещает другой.

Ограниченность. Это свойство связано с введением ограничений на число меток в позициях.
Позиция pi называется k-ограниченной, если количество фишек в ней не может превышать целого числа k, т. е.
Сеть Петри называется ограниченной, если все ее позиции ограничены.
Безопасность. Позиция сети Петри называется безопасной, если число фишек в ней никогда не превышает единицы. Сеть Петри безопасна, если безопасны все ее позиции. Это свойство важно при интерпретации позиций как простых условий: если в позиции есть фишка, то условие выполняется, если нет, то не выполняется. Безопасную позицию можно реализовать одним триггером.
4 Свойства сетей Петри

Сохраняемость.
Сеть Петри С = (P, T, F, H, μ0) называется строго сохраняющей, если сумма фишек по всем позициям остается строго постоянной в процессе выполнения сети, т. е. для всех возможных маркировок μ'
Живость.
Под живостью перехода ti понимают принципиальную возможность его срабатывания при функционировании сети Петри. Тупик в сети Петри – это переход (или множество переходов), который в имеющейся маркировке μ' и в последующих достижимых из μ' маркировках не разрешен.

Достижимость.
Свойство достижимости используется при установлении возможности возникновения некоторой ситуации в системе.
Пусть проверяемая ситуация описывается разметкой μ'. Возникает задача: достижима ли маркировка μ' из начальной маркировки μ0 данной сети Петри.
Задача достижимости является одной из наиболее важных задач анализа сетей Петри.

5 Анализ сетей Петри
Основная задача анализа сетей Петри – задача достижимости: достижима ли маркировка μ' из начальной маркировки μ0 данной сети Петри.
Первый основан на построении дерева достижимости. Дерево достижимости – это ориентированное корневое дерево, вершинам которого, соответствуют возможные маркировки, а дугам – переходы.
Начальная маркировка соответствует корню дерева. Из него исходят дуги, соответствующие разрешенным переходам.
На каждом шаге строится очередной ярус дерева. Дерево представляет все возможные последовательности запусков переходов. Всякий путь, начинающийся в корне, соответствует допустимой последовательности переходов.

Другой подход к анализу сетей Петри называется матричным и основан на их матричном представлении.
Пусть осуществляется последовательность срабатываний переходов
В результате получится маркировка
– вектор целых положительных чисел, r-й элемент которого показывает сколько раз сработал переход tir в цепочке срабатываний, переводящей из μ0 в μ‘.

Для того чтобы существовала последовательность срабатываний σ, которая приводит из μ0 в μ', необходимо, чтобы вектор f(σ) являлся неотрицательным целым решением матричного уравнения
Если это уравнение не имеет решений, разметка μ' является недостижимой на данной сети из μ0.
Недоcтатки матричного анализа в том, что вектор срабатывания f(σ) не дает информации о порядке срабатывания переходов, кроме того, возможны недействительные решения уравнения, т. е. получаем некоторую последовательность переходов, которая не возможна.

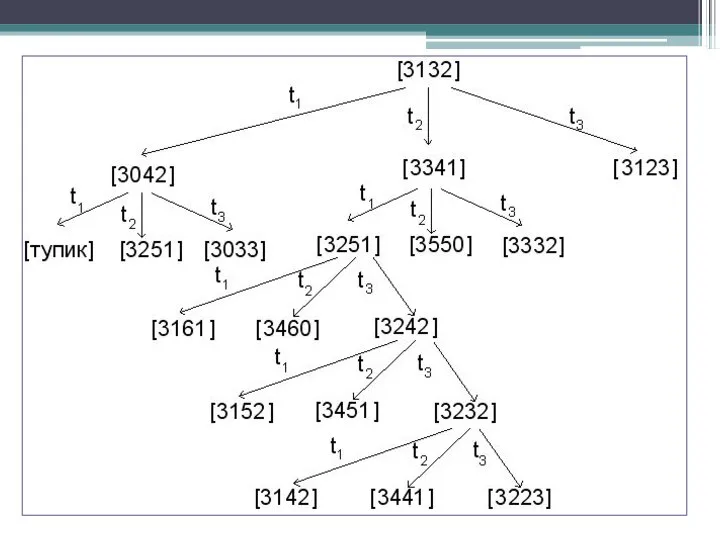
Пример 2 Проверим, является ли достижимой одна из маркировок, полученных на пятом шаге построения дерева, составив и решив матричные уравнения.
Уравнение принимает вид
Перенесем μ0 в левую часть и выполним умножение, тогда
Приравняем составляющие векторов

Система имеет решение x1 = 2; x2 = 1; x3 = 2.
Это значит, что исследуемая маркировка достижима и в последовательности срабатываний переход t1 срабатывает два раза, переход t2 срабатывает один раз, переход t3 - два раза.

6 Подклассы и расширения сетей Петри
К подклассу автоматных графов относят сети Петри, в которых каждый переход имеет одну входную и одну выходную позиции. Такие сети описывают последовательные процессы и как математическая модель эквивалентны конечным автоматам.
В автоматных графах легко представить конфликтные ситуации, но нельзя моделировать создание и уничтожение фишек, необходимых для моделирования параллельных процессов или ожидания.

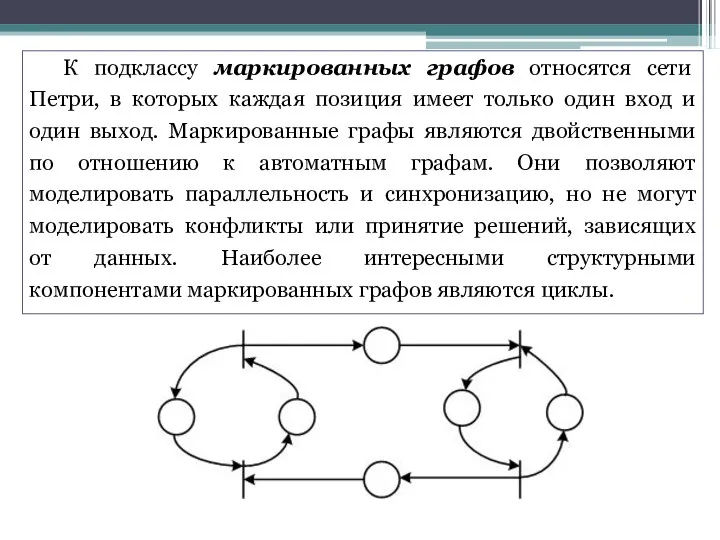
К подклассу маркированных графов относятся сети Петри, в которых каждая позиция имеет только один вход и один выход. Маркированные графы являются двойственными по отношению к автоматным графам. Они позволяют моделировать параллельность и синхронизацию, но не могут моделировать конфликты или принятие решений, зависящих от данных. Наиболее интересными структурными компонентами маркированных графов являются циклы.

К подклассу устойчивых сетей Петри относятся сети, которые обладают следующим свойством: если при любой маркировке μ два любых перехода ti и tj оказываются разрешенными, то срабатывание одного из них не исключает возможности срабатывания другого перехода.
Временные сети Петри позволяют отразить в модели временные параметры системы. Если моделируемое событие имеет отличную от нуля длительность, как например, событие «задание обрабатывается», то оно представляется в виде двух мгновенных событий типа «начало события», «конец события» и условия «событие происходит» .
Считается, что события происходят неодновременно. Позиции во временных сетях взвешиваются временем выполнения.