- Главная
- Информатика
- Методы класса как подпрограммы. Решение нелинейных уравнений

Содержание
- 2. Подпрограмма. Процедура. Функция. Метод Машинный язык: Подпрограмма принимает и возвращает значения через глобальные переменные, регистры или
- 3. Подпрограмма. Процедура. Функция. Метод Машинный язык: Подпрограмма принимает и возвращает значения через глобальные переменные, регистры или
- 4. Решение нелинейного уравнения public partial class Form1 : Form { double x1, x2, eps; int N;
- 5. Решение нелинейного уравнения double y_x(double x) { return Math.Pow(Math.Cos(x), 1/3.0); } void metod_iteraziy() { textBox2.Text =
- 6. Решение нелинейного уравнения
- 8. Скачать презентацию
Слайд 2Подпрограмма. Процедура. Функция. Метод
Машинный язык:
Подпрограмма принимает и возвращает значения через глобальные переменные,
Подпрограмма. Процедура. Функция. Метод
Машинный язык: Подпрограмма принимает и возвращает значения через глобальные переменные,

Pascal: Процедура = подпрограмма Функция = подпрограмма, возвращающая значение
C: Функция может возвращать или не возвращать значение (процедур нет)
C#, Java и другие: Данные и код инкапсулированы в классы. Инкапсулированные подпрограммы называются методами.
// пример вызова процедуры на языке Assebmler
mov ax, 0
mov dx, 123
call my_proc
// пример вызова процедур и функций на языке Pascal
writeln;
y := sin(x);
// пример вызова функций на языке Си
getch();
c = getch();
y = sin(x);
// пример вызова методов на языке C#
textBox1.Hide();
x = r.NextDouble();
y = Math.Sin(x);
Слайд 3Подпрограмма. Процедура. Функция. Метод
Машинный язык:
Подпрограмма принимает и возвращает значения через глобальные переменные,
Подпрограмма. Процедура. Функция. Метод
Машинный язык: Подпрограмма принимает и возвращает значения через глобальные переменные,
Pascal: Процедура = подпрограмма Функция = подпрограмма, возвращающая значение
C: Функция может возвращать или не возвращать значение (процедур нет)
C#, Java и другие: Данные и код инкапсулированы в классы. Инкапсулированные подпрограммы называются методами.
// пример вызова процедуры на языке Assebmler
mov ax, 0
mov dx, 123
call my_proc
// пример вызова процедур и функций на языке Pascal
writeln;
y := sin(x);
// пример вызова функций на языке Си
getch();
c = getch();
y = sin(x);
// пример вызова методов на языке C#
textBox1.Hide();
x = r.NextDouble();
y = Math.Sin(x);
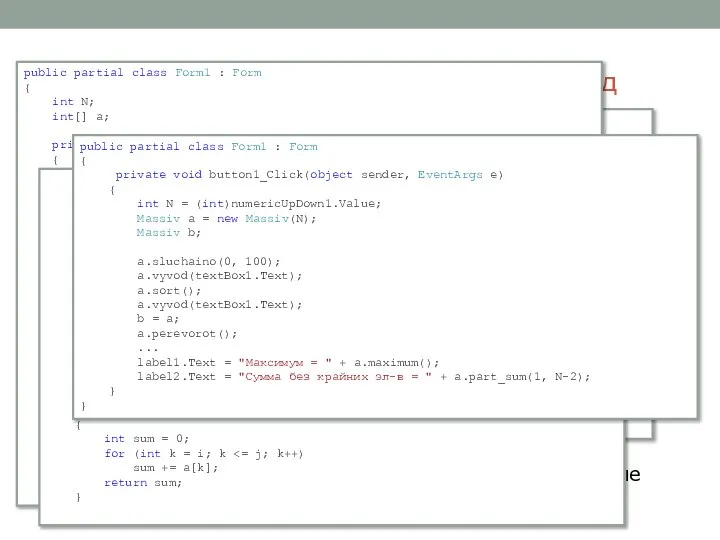
public partial class Form1 : Form
{
int N;
int[] a;
private void button1_Click(object sender, EventArgs e)
{
N = (int)numericUpDown1.Value;
a = new int[N];
massiv_sluchaino(0, 100);
massiv_v_textbox();
massiv_sort();
massiv_v_textbox();
massiv_perevorot();
massiv_v_textbox();
}
void massiv_v_textbox()
{
for (int i = 0; i < N; i++)
textBox1.Text += String.Format("a[{0}] = {1}\r\n", i + 1, a[i]);
textBox1.Text += "\r\n";
}
void massiv_sluchaino(int min, int max)
{
...
}
private void button1_Click(object sender, EventArgs e)
{
...
label1.Text = "Максимум = " + massiv_max();
label2.Text = "Сумма без крайних эл-в = " + massiv_part_sum(1, N-2);
}
int massiv_max()
{
int max = int.MinValue;
for (int i = 0; i < N; i++)
if (a[i] > max) max = a[i];
return max;
}
int massiv_part_sum(int i, int j)
{
int sum = 0;
for (int k = i; k <= j; k++)
sum += a[k];
return sum;
}
public partial class Form1 : Form
{
private void button1_Click(object sender, EventArgs e)
{
int N = (int)numericUpDown1.Value;
Massiv a = new Massiv(N);
Massiv b;
a.sluchaino(0, 100);
a.vyvod(textBox1.Text);
a.sort();
a.vyvod(textBox1.Text);
b = a;
a.perevorot();
...
label1.Text = "Максимум = " + a.maximum();
label2.Text = "Сумма без крайних эл-в = " + a.part_sum(1, N-2);
}
}
Слайд 4
Решение нелинейного уравнения
public partial class Form1 : Form
{
double x1, x2, eps;
Решение нелинейного уравнения
public partial class Form1 : Form
{
double x1, x2, eps;
private void button1_Click(object sender, EventArgs e)
{
x1 = Convert.ToDouble(textBox4.Text); // начало отрезка изоляции
x2 = Convert.ToDouble(textBox5.Text); // конец отрезка изоляции
eps = Convert.ToDouble(textBox6.Text); // точность
N = Convert.ToInt32(textBox7.Text); // предельное число итераций
metod_del_popolam();
//metod_iteraziy();
//metod_Newtona();
}
double y(double x)
{
return Math.Cos(x) - x * x * x;
}
void metod_del_popolam()
{
...
}
}
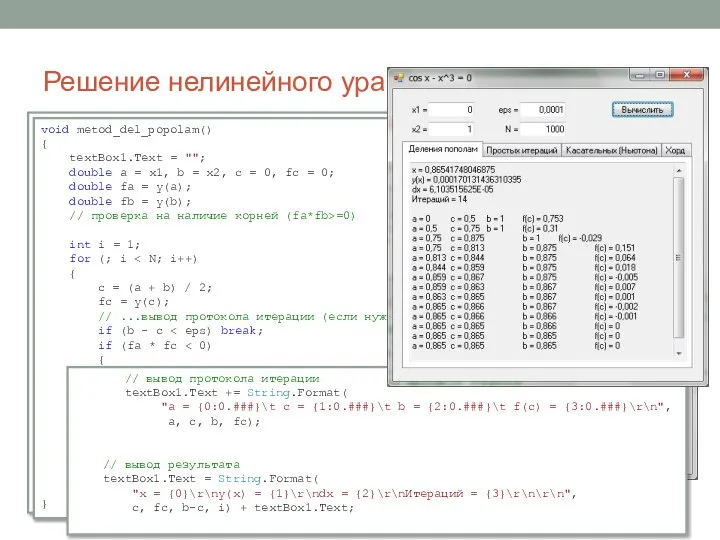
void metod_del_popolam()
{
textBox1.Text = "";
double a = x1, b = x2, c = 0, fc = 0;
double fa = y(a);
double fb = y(b);
// проверка на наличие корней (fa*fb>=0)
int i = 1;
for (; i < N; i++)
{
c = (a + b) / 2;
fc = y(c);
// ...вывод протокола итерации (если нужно)
if (b - c < eps) break;
if (fa * fc < 0)
{
b = c; fb = fc;
}
else
{
a = c; fa = fc;
}
}
// вывод или возврат результата
}
// вывод протокола итерации
textBox1.Text += String.Format(
"a = {0:0.###}\t c = {1:0.###}\t b = {2:0.###}\t f(c) = {3:0.###}\r\n",
a, c, b, fc);
// вывод результата
textBox1.Text = String.Format(
"x = {0}\r\ny(x) = {1}\r\ndx = {2}\r\nИтераций = {3}\r\n\r\n",
c, fc, b-c, i) + textBox1.Text;
Слайд 5
Решение нелинейного уравнения
double y_x(double x)
{
return Math.Pow(Math.Cos(x), 1/3.0);
}
void metod_iteraziy()
{
textBox2.Text = "";
Решение нелинейного уравнения
double y_x(double x)
{
return Math.Pow(Math.Cos(x), 1/3.0);
}
void metod_iteraziy()
{
textBox2.Text = "";

int i = 1;
for (; i < N; i++)
{
x = y_x(prev_x);
// ...вывод протокола итерации(если нужно)
if (Math.Abs(prev_x - x) < eps)
break;
prev_x = x;
}
// ...вывод или возврат результата
}
double dy(double x)
{
return - Math.Sin(x) - 3 * x * x;
}
void metod_Newtona()
{
textBox3.Text = "";
double x = (x1+x2)/2, prev_x = x;
int i = 1;
for (; i < N; i++)
{
x = prev_x - y(prev_x) / dy(prev_x);
// ...вывод протокола итерации(если нужно)
if (Math.Abs(prev_x - x) < eps)
break;
prev_x = x;
}
// ...вывод или возврат результата
}
void metod_hord()
{
textBox8.Text = "";
double a = x1, b = x2, c = 0;
int i = 1;
for (; i < N; i++)
{
c = a - y(a) * (a - b) / (y(a) - y(b));
// ...вывод протокола итерации(если нужно)
if (Math.Abs(c - a) < eps)
break;
b = a;
a = c;
}
// ...вывод или возврат результата
}
Слайд 6
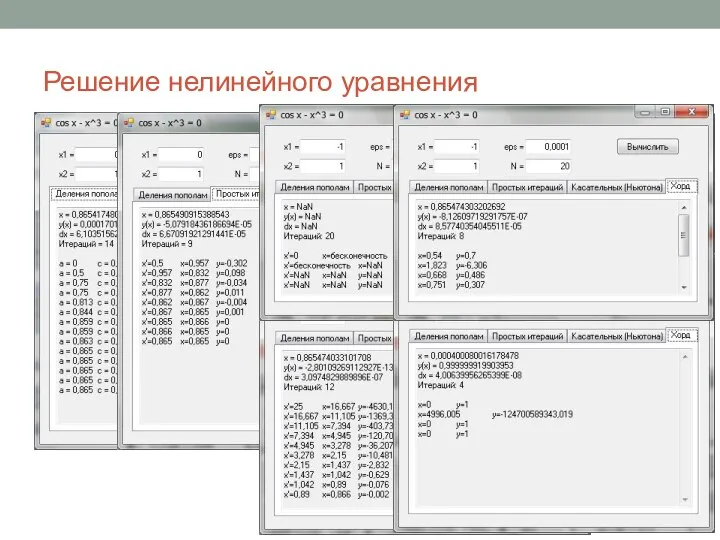
Решение нелинейного уравнения
Решение нелинейного уравнения
 10 главных тенденций разработки программного обеспечения в 2021 году
10 главных тенденций разработки программного обеспечения в 2021 году Человек в виртуальном пространстве
Человек в виртуальном пространстве ВК: продвижение страницы
ВК: продвижение страницы Присоединение Средней Азии. Классификация изданий. Итоговая информативность
Присоединение Средней Азии. Классификация изданий. Итоговая информативность Element list page
Element list page Виды информации (интерактивный тест, 8 класс)
Виды информации (интерактивный тест, 8 класс) Взаимодействие с Федеральным казначейством и Мировыми судьями
Взаимодействие с Федеральным казначейством и Мировыми судьями 9-1-4 (2)
9-1-4 (2) Операционная система Windows
Операционная система Windows Презентация на тему Безопасность общения в социальных сетях
Презентация на тему Безопасность общения в социальных сетях 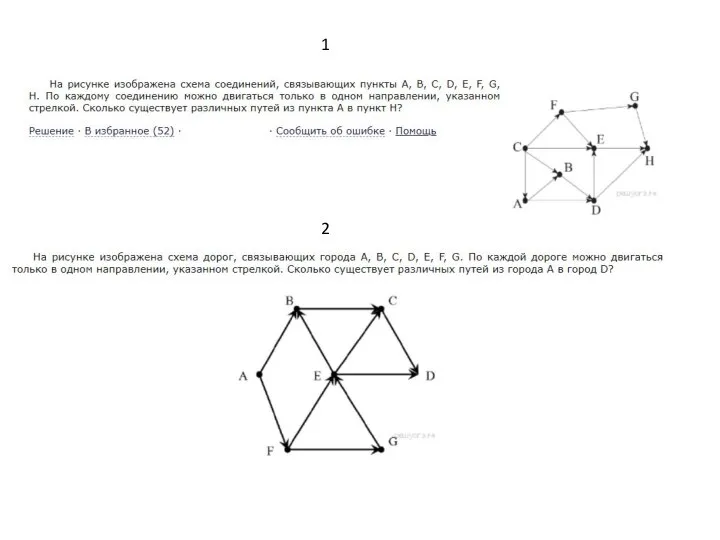 Графы. Схемы
Графы. Схемы 390561 (1)
390561 (1) Хранение информации. Память человека и память человечества. Оперативная и долговременная память. Информатика, 5 класс
Хранение информации. Память человека и память человечества. Оперативная и долговременная память. Информатика, 5 класс Символ собака
Символ собака Primenenie_trekhmernoy_grafiki
Primenenie_trekhmernoy_grafiki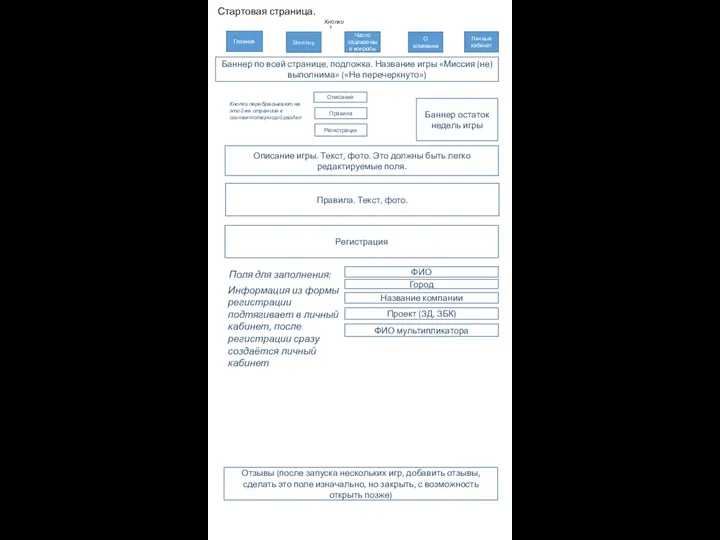 Техническое задание. Игра Миссия (не) выполнима
Техническое задание. Игра Миссия (не) выполнима Системы координат. Справочная система. Занятие №3
Системы координат. Справочная система. Занятие №3 Виды и форматы электронных изданий
Виды и форматы электронных изданий Основы программирования. Анализ трудоемкости алгоритмов
Основы программирования. Анализ трудоемкости алгоритмов Контрольное тестирование
Контрольное тестирование Статический анализатор clang
Статический анализатор clang Мультимедиа. Классификация
Мультимедиа. Классификация Программное обеспечение компьютера (ПО)
Программное обеспечение компьютера (ПО) Доброе утро 3.0
Доброе утро 3.0 Культура РФ. Установка счётчика КУЛЬТУРА.РФ на сайт МКУК ПЦБС
Культура РФ. Установка счётчика КУЛЬТУРА.РФ на сайт МКУК ПЦБС Кодирование данных, комбинаторика, системы счисления (Задача 8)
Кодирование данных, комбинаторика, системы счисления (Задача 8) Как обновить формы
Как обновить формы Языки программирования и их развитие
Языки программирования и их развитие