Множественный тип данных. Множество в языке Паскаль

Базовый тип
это совокупность значений, из которых могут быть образованы множества. В качестве базового типа может быть использован любой тип, кроме вещественного.
Значение переменной множественного типа может содержать любое количество различных элементов базового типа – от нуля элементов (пустое множество) до всех возможных значений базового типа (всего может быть не более 256 различных элементов).

Описание
В разделе описания типов:
Type <имя типа> = set of <тип элементов>;
Var <имя множества>: <имя типа>;
В разделе описания переменных:
Var < имя множества >: set of < тип элементов >;
Пример:
Type mnog_char = set of char;
Var mn1: mnog_char;
mn2: set of char;
mn3: set of ‘A’..’Z’;
s1: set of byte;
s2: set of 1000 .. 1200;

Формирование множеств
В программе элементы множества задаются в квадратных скобках, через запятую. Если элементы идут подряд друг за другом, то можно использовать диапазон.
Пример:
Type digit = set of 1..5;
Var s: digit;
Переменная s может принимать значения, состоящие из любой совокупности целых чисел от 1 до 5:
[ ] – пустое множество;
[1], [2], [3], [4], [5] - одноэлементные множества;
[1,2],…[4,5] – двухэлементные; [1, 2, 3] – трехэлементное;
[1, 2, 3, 4],… [2, 3, 4, 5] – четырехэлементные;
[1, 2, 3, 4, 5] – полное множество (взяты все элементы базового типа)

Операции над множествами
Объединением двух множеств называется множество элементов, принадлежащих обоим множествам. Знак операции – « + ».
Примеры:
[‘A’, ’F’] + [‘B’, ’D’] = [‘A’,’F’,‘B’, ’D’];
[1..3, 5, 7, 11] + [3..8,10, 12, 15..20] = [1..8, 10..12, 15..20];
A1:=[‘a’, .. ‘z’]; A1:= A1 + [‘A’]; - к множеству A1 добавляем элемент. Тогда A1 = [‘A’, ‘a’ .. ‘z’];

Пересечением двух множеств называется множество элементов, принадлежащих одновременно и первому, и второму множеству, т.е. это общие элементы. Знак операции – « * ».
Примеры:
[‘A’, ’F’] * [‘B’, ’D’] =[ ] – так как общих элементов нет;
[1..3, 5, 7, 11] * [3..8,10, 12, 15..20] = [3, 5, 7];
S1:=[1 .. 5, 9]; S2:= [3 .. 7, 12]; S:= S1 * S2;
то результат выполнения S =[3 .. 5];
Операции над множествами

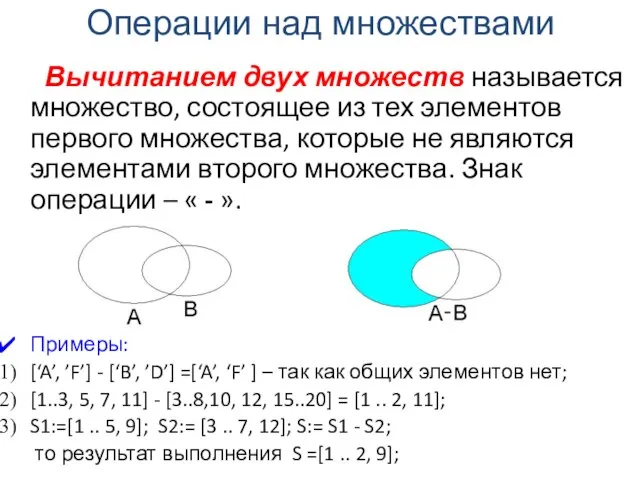
Вычитанием двух множеств называется множество, состоящее из тех элементов первого множества, которые не являются элементами второго множества. Знак операции – « - ».
Примеры:
[‘A’, ’F’] - [‘B’, ’D’] =[‘A’, ‘F’ ] – так как общих элементов нет;
[1..3, 5, 7, 11] - [3..8,10, 12, 15..20] = [1 .. 2, 11];
S1:=[1 .. 5, 9]; S2:= [3 .. 7, 12]; S:= S1 - S2;
то результат выполнения S =[1 .. 2, 9];
Операции над множествами

Операция определения принадлежности элемента множеству
in – служебное слово. Логическая операция имеет результат true, если значение входит в множество и false в противном случае.
Примеры:
5 in [3 .. 7] => true, т.к 5 принадлежит [3 .. 7];
‘a’ in [‘A’ ..’Z’] => false, т.к. маленькой латинской буквы ‘a’ нет среди больших латинских букв.
Примечание. Оператор вида:
if (ch=‘a’) or (ch=‘b’) or (ch=‘x’) or (ch=‘y’) then s;
может быть переписан в компактной наглядной форме: if ch in [‘a’,’b’,’x’,’y’] then s;

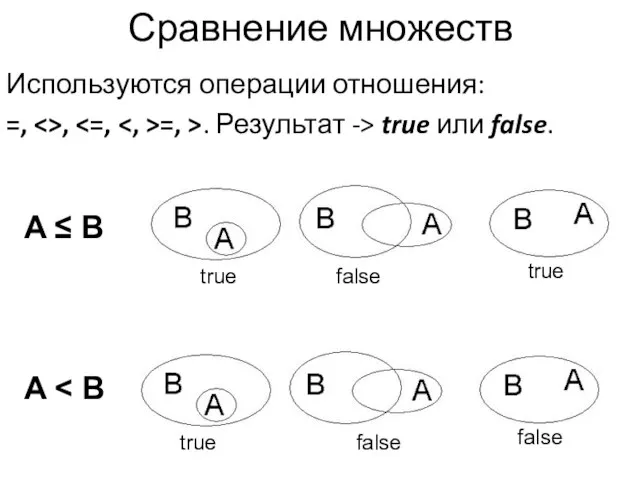
Сравнение множеств
Используются операции отношения:
=, <>, <=, <, >=, >. Результат -> true или false.
true
false
true
A ≤ B
true
false
false
A < B

Пример 1.
Составить программу выделения из множества целых чисел от 1 до 30 следующих множеств:
множества чисел кратных 2;
множества чисел кратных 3;
множества чисел кратных 6;
множества чисел кратных 2 или 3;
Вопросы:
Сколько множеств надо описать? Какого они типа?
Какое первоначальное значение множеств?
Как формируются множества?
Как осуществить вывод сформированных множеств?

program Ex1;
const n=30;
type mn=set of 1..n;
var n2,n3,n6,n23: mn; {n2 – множество чисел кратных 2,} { n3 - кратных 3}
k:integer; {n6 - кратных 6, n23 - кратных 2 или 3}
procedure Print(m:mn);
var i:integer;
Begin
for i:=1 to n do If i in m then write(i:3);
writeln;
end;

begin
n2:=[ ]; n3:=[ ]; {начальное значение множества}
for k:=1 to n do {формирование n2 и n3}
begin
if k mod 2=0 then n2:=n2+[k];
if k mod 3=0 then n3:=n3+[k]
end;
n6:=n2*n3;{числа кратные 6, это те, которые кратны и 2, и 3,} {поэтому это пересечение двух первых множеств}
n23:=n2+n3; {а числа кратные 2 или 3 – это объединение этих же множеств}
writeln(‘числа, кратные 2'); print(n2);
writeln(' числа, кратные 3'); print(n3);
writeln(' числа, кратные 6'); print(n6);
writeln(' числа, кратные 2 или 3'); print(n23);
readln;
end.

Домашнее задание.
Изменить программу так, чтобы результатом ее работы являлось множество чисел, делящихся на 3, но не делящихся на 2.

Задача.
Дано натуральное число n.составить программу, печатающую все цифры, не входящие в десятичную запись данного натурального числа в порядке возрастания.