Содержание
- 2. Моделирование § 6. Модели и моделирование
- 3. Что такое модель? модели чего? автомобиль Земля кристаллическая решётка корабль дом оригиналы объекты (самолет, дом, ядро
- 4. Что такое модель? оригинал не существует древний Египет последствия ядерной войны (Н.Н. Моисеев, 1966) исследование оригинала
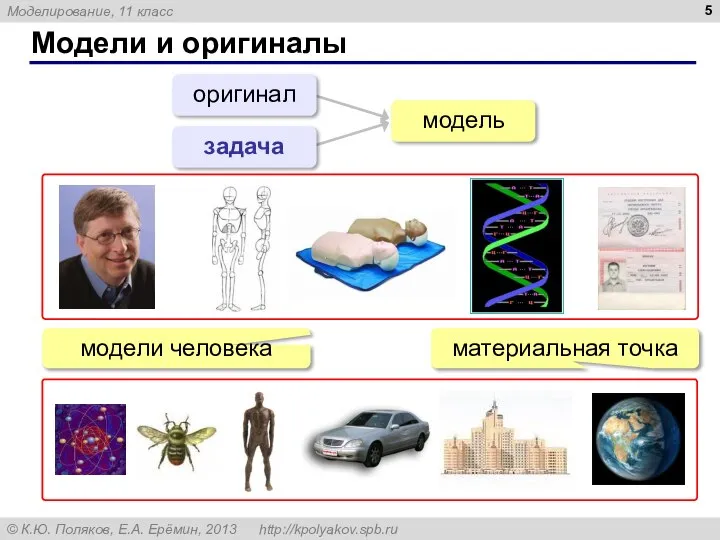
- 5. Модели и оригиналы оригинал задача модель материальная точка модели человека
- 6. Модели и моделирование Модель – это объект, который обладает существенными свойствами другого объекта, процесса или явления
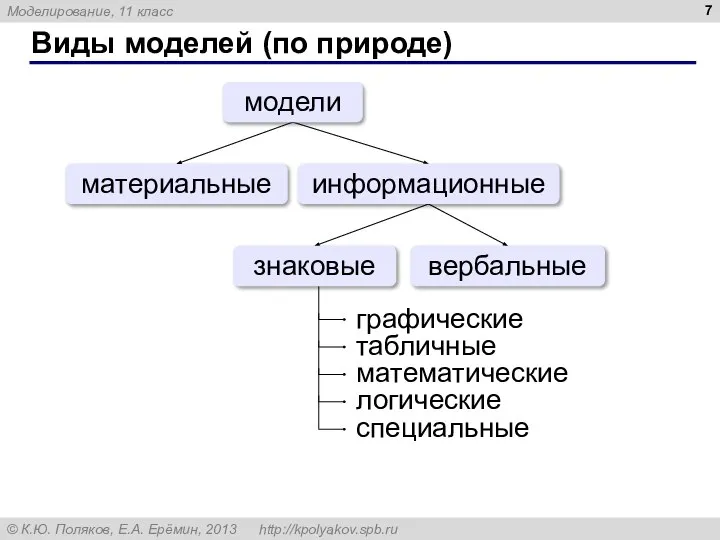
- 7. Виды моделей (по природе) материальные вербальные модели знаковые информационные
- 8. Виды моделей (по фактору времени) статические – описывают оригинал в заданный момент времени силы, действующие на
- 9. Виды моделей (по характеру связей) детерминированные – при одинаковых исходных данных всегда получается тот же результат
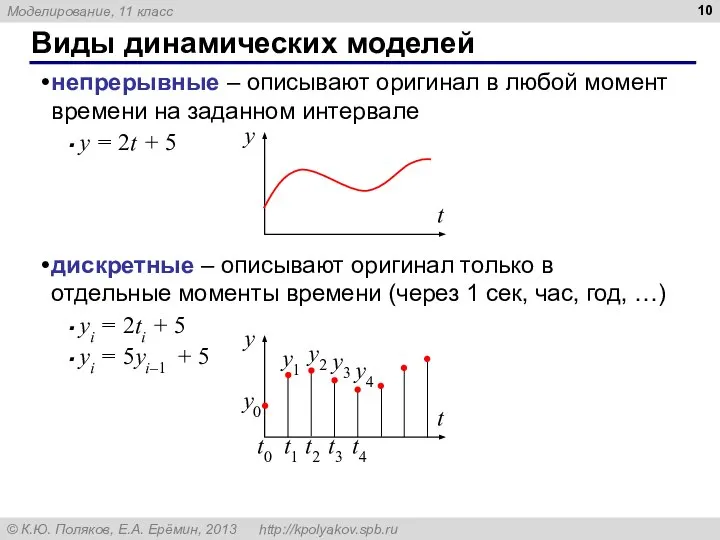
- 10. Виды динамических моделей непрерывные – описывают оригинал в любой момент времени на заданном интервале y =
- 11. Имитационные модели нельзя заранее вычислить или предсказать поведение системы, но можно имитировать её реакцию на внешние
- 12. Игровые модели экономические ситуации военные действия спортивные игры тренинги персонала Игровые модели учитывают действия противников.
- 13. Адекватность Адекватность – это совпадение существенных свойств модели и оригинала в данной задаче. Модель всегда отличается
- 14. Моделирование § 7. Системный подход в моделировании
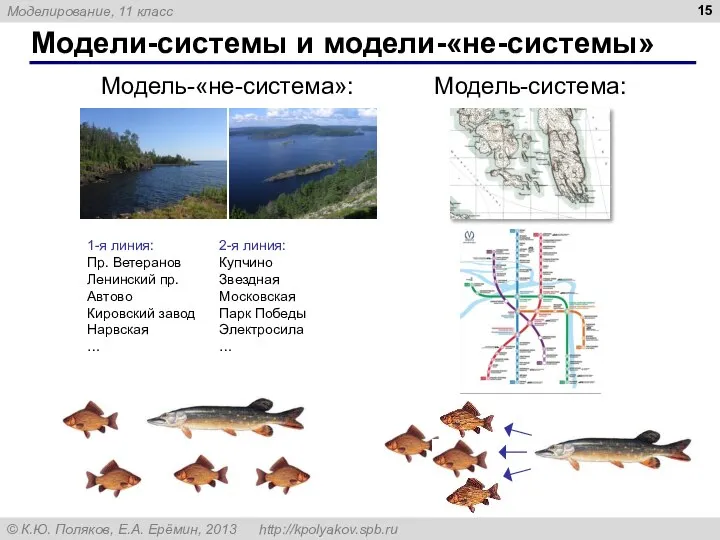
- 15. Модели-системы и модели-«не-системы» Модель-система: Модель-«не-система»: 1-я линия: Пр. Ветеранов Ленинский пр. Автово Кировский завод Нарвская …
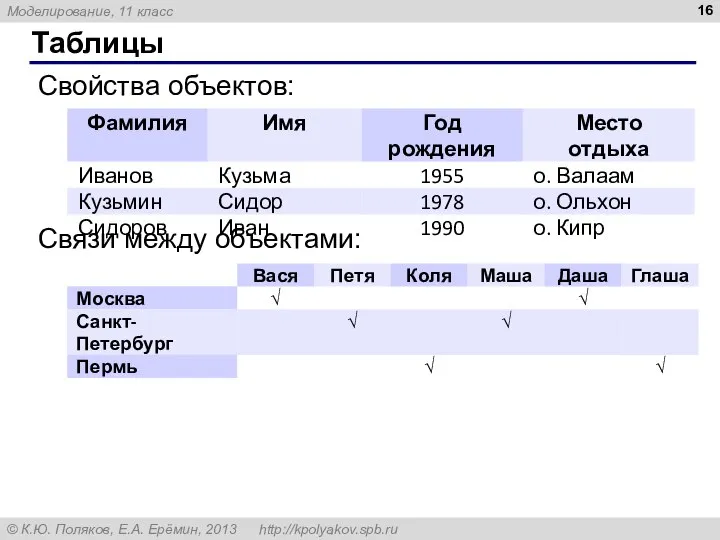
- 16. Таблицы Свойства объектов: Связи между объектами:
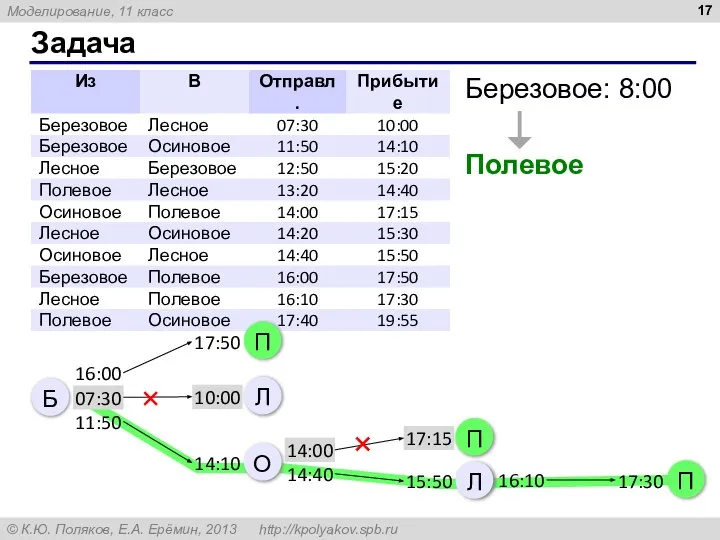
- 17. Задача Березовое: 8:00 Полевое Б 16:00 07:30 11:50 14:00 14:40 16:10
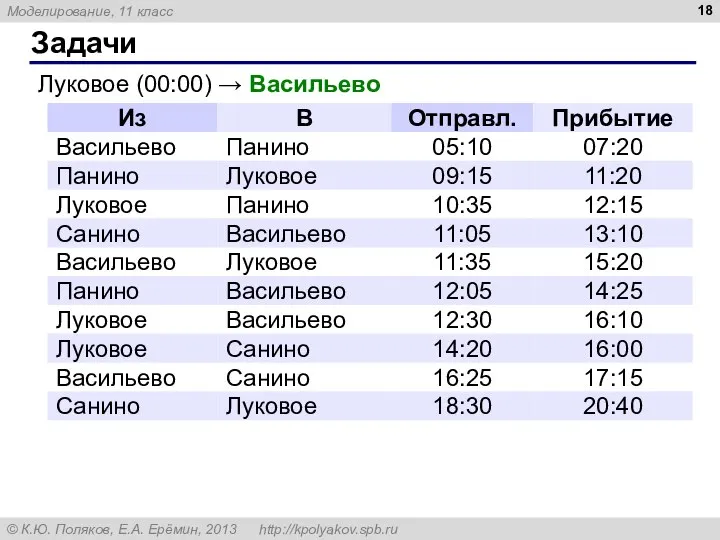
- 18. Задачи Луковое (00:00) → Васильево
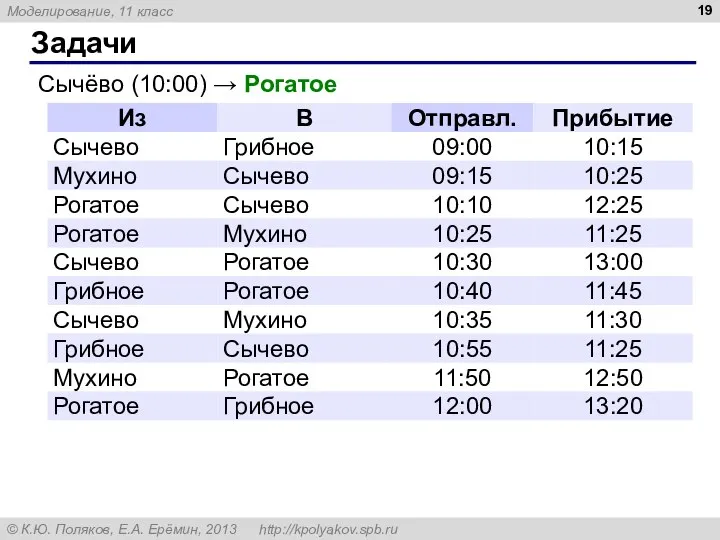
- 19. Задачи Сычёво (10:00) → Рогатое
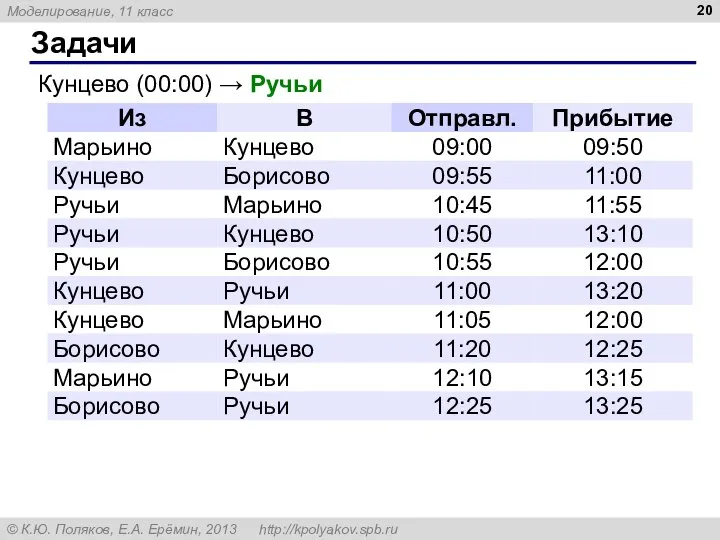
- 20. Задачи Кунцево (00:00) → Ручьи
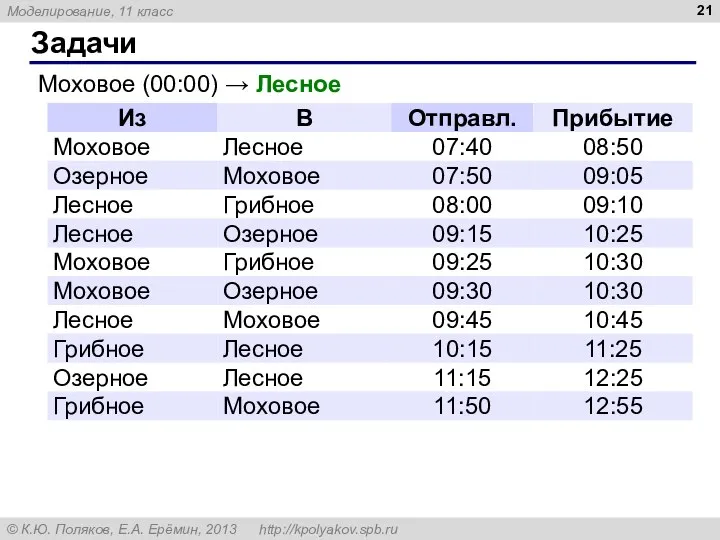
- 21. Задачи Моховое (00:00) → Лесное
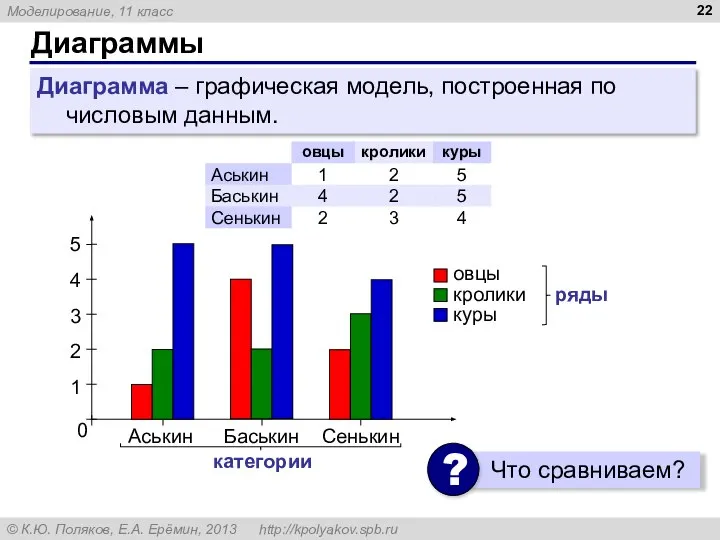
- 22. Диаграммы Диаграмма – графическая модель, построенная по числовым данным.
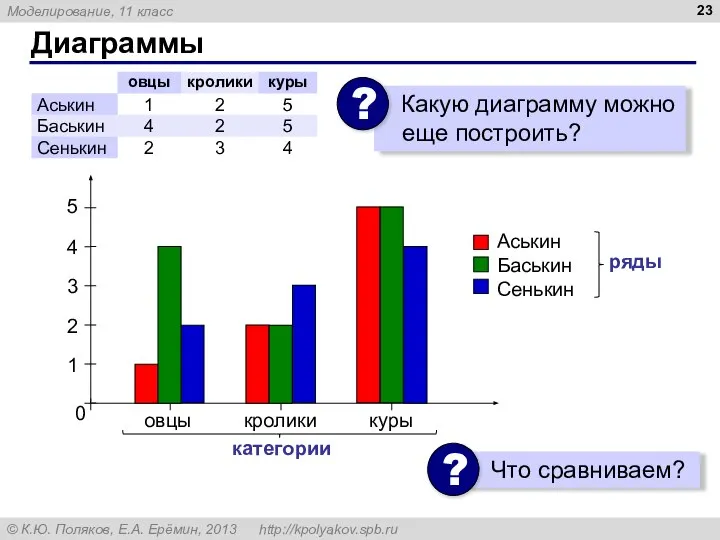
- 23. Диаграммы
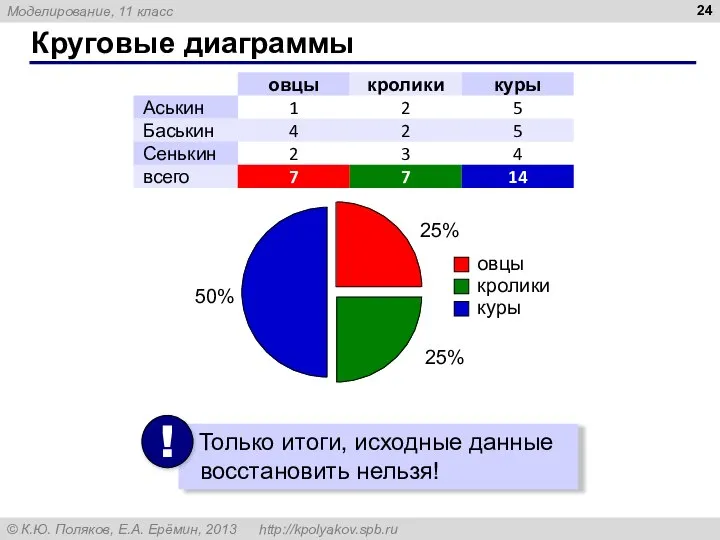
- 24. Круговые диаграммы
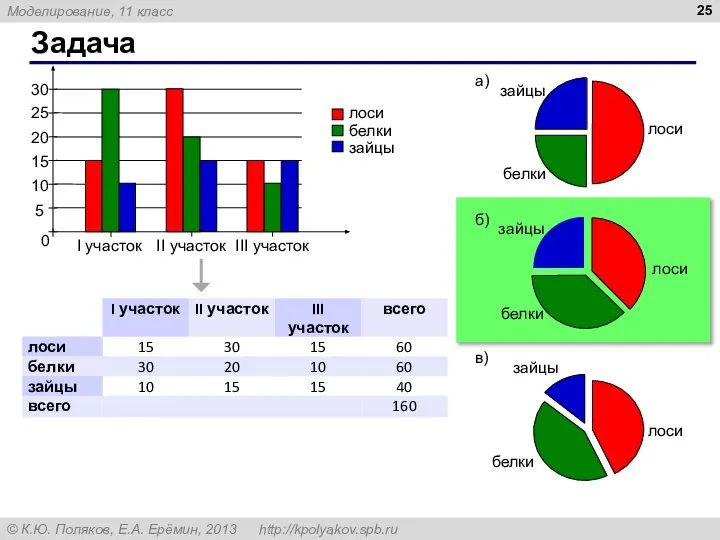
- 25. Задача
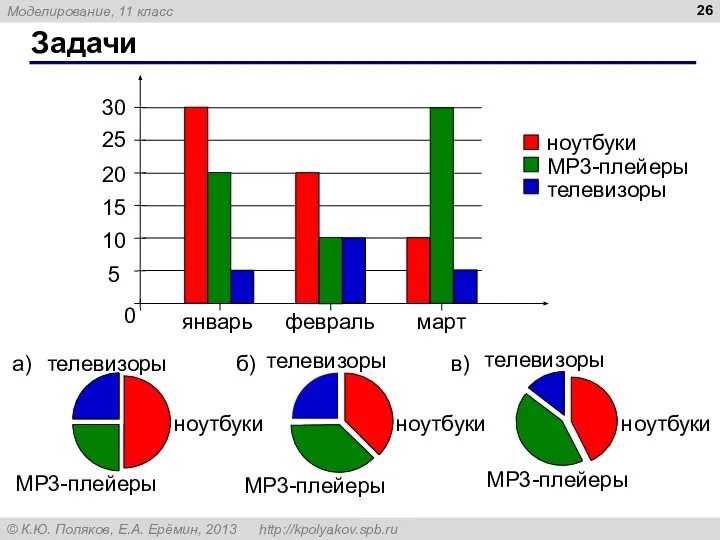
- 26. Задачи
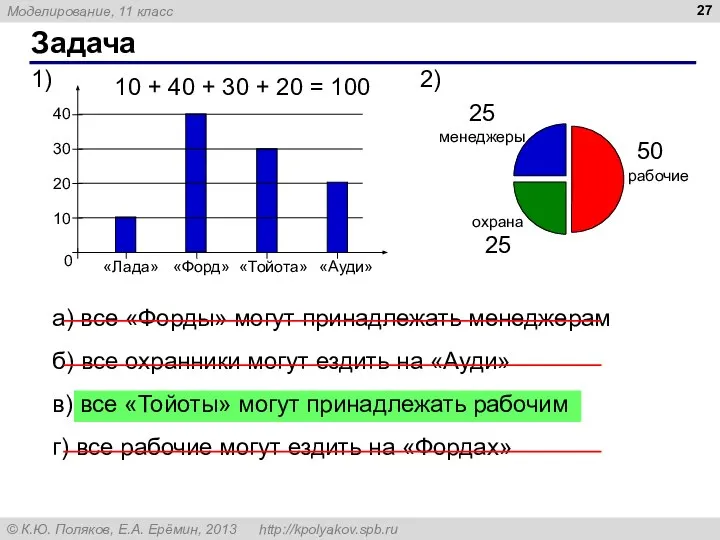
- 27. Задача а) все «Форды» могут принадлежать менеджерам б) все охранники могут ездить на «Ауди» в) все
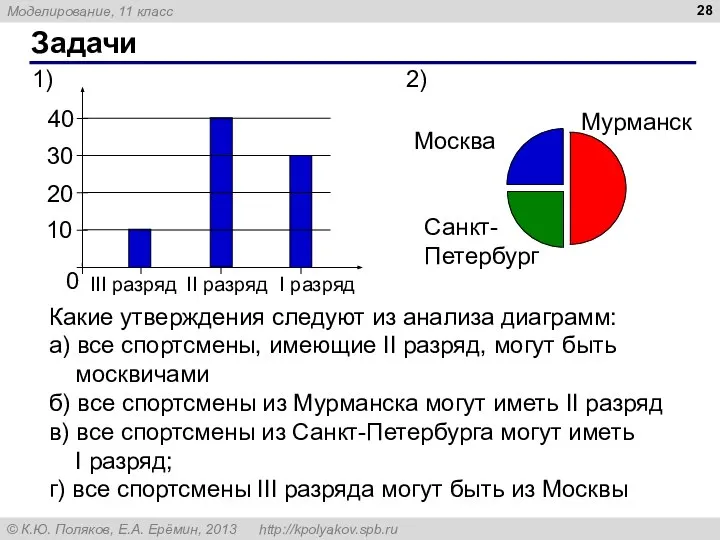
- 28. Задачи Какие утверждения следуют из анализа диаграмм: а) все спортсмены, имеющие II разряд, могут быть москвичами
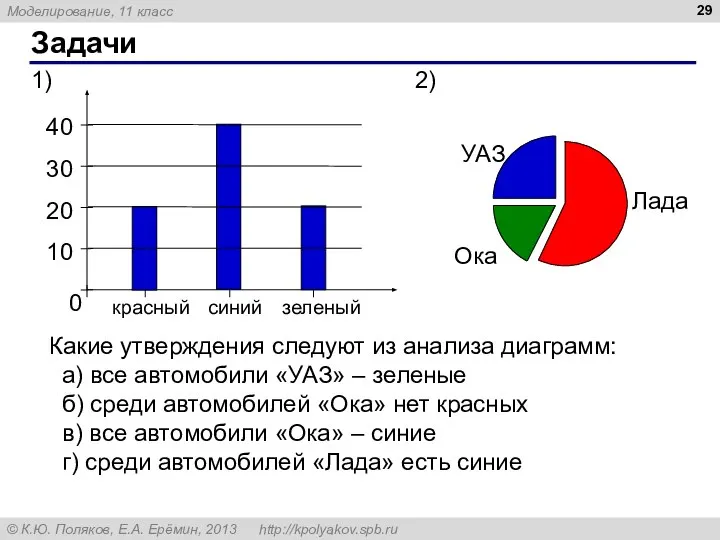
- 29. Задачи Какие утверждения следуют из анализа диаграмм: а) все автомобили «УАЗ» – зеленые б) среди автомобилей
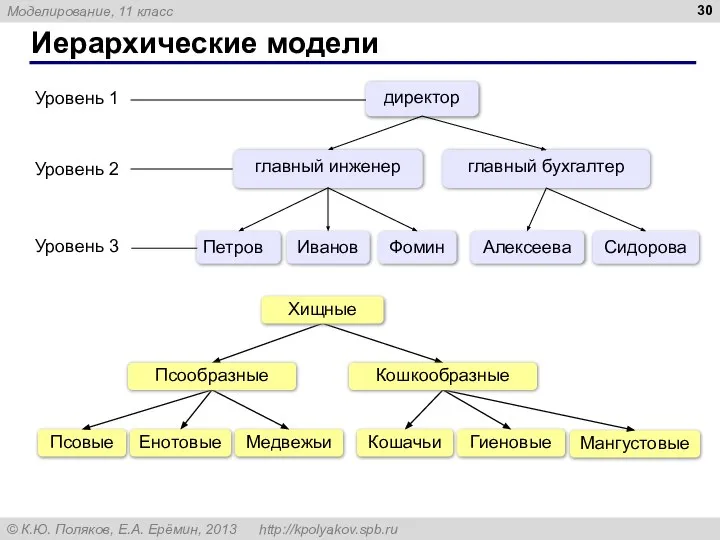
- 30. Иерархические модели
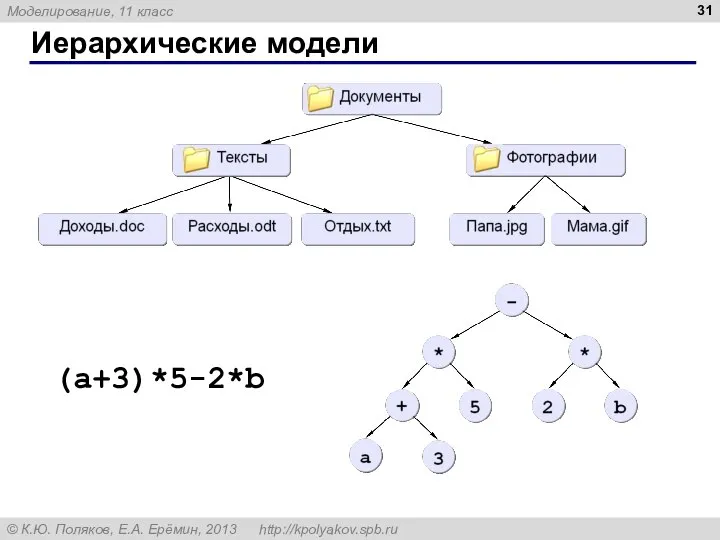
- 31. Иерархические модели (a+3)*5-2*b
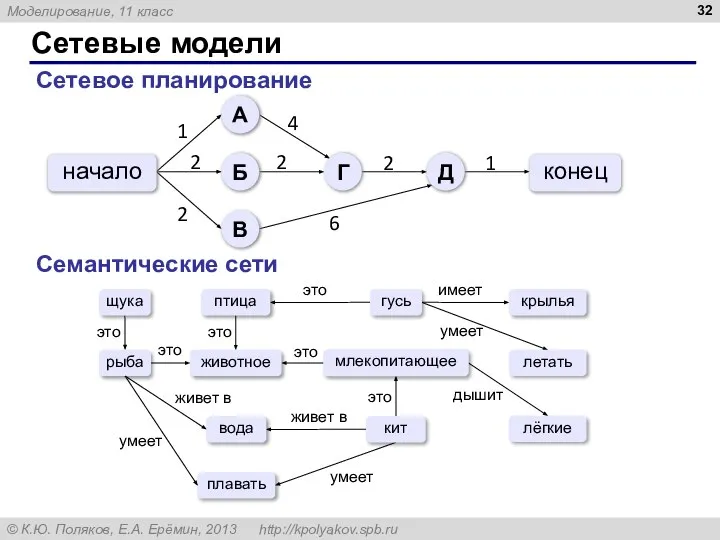
- 32. Сетевые модели Сетевое планирование Семантические сети
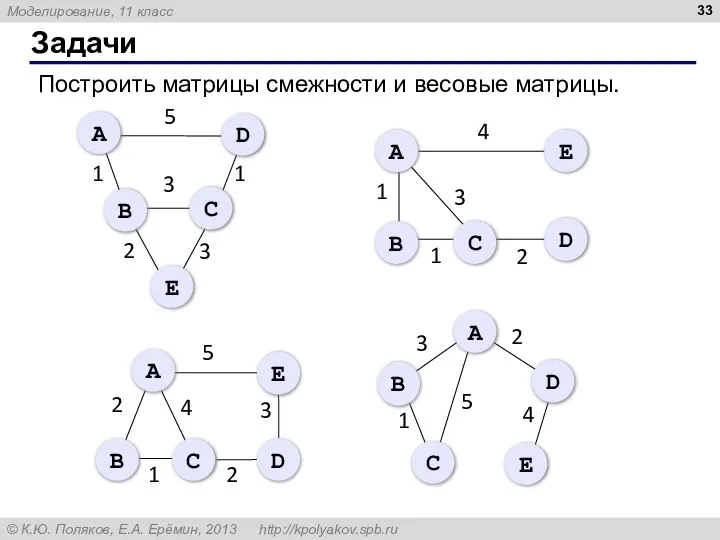
- 33. Задачи Построить матрицы смежности и весовые матрицы.
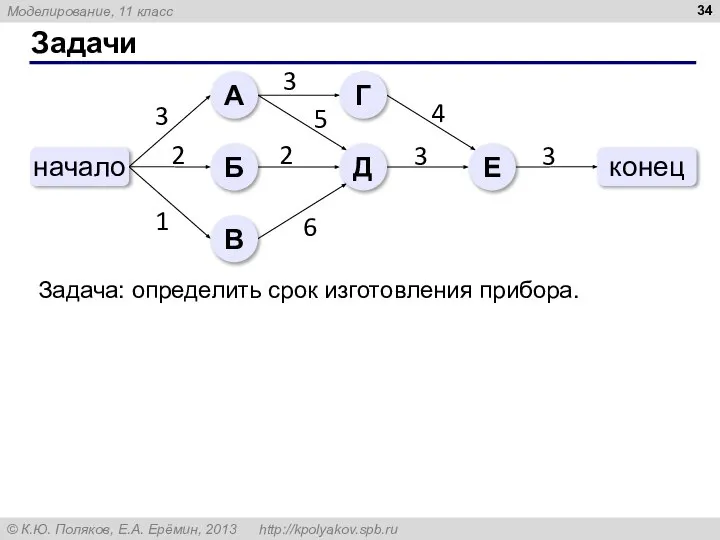
- 34. Задачи Задача: определить срок изготовления прибора.
- 35. Игровые стратегии Задача: найти стратегию (алгоритм игры), который позволит получить лучший результат, если соперники играют безошибочно.
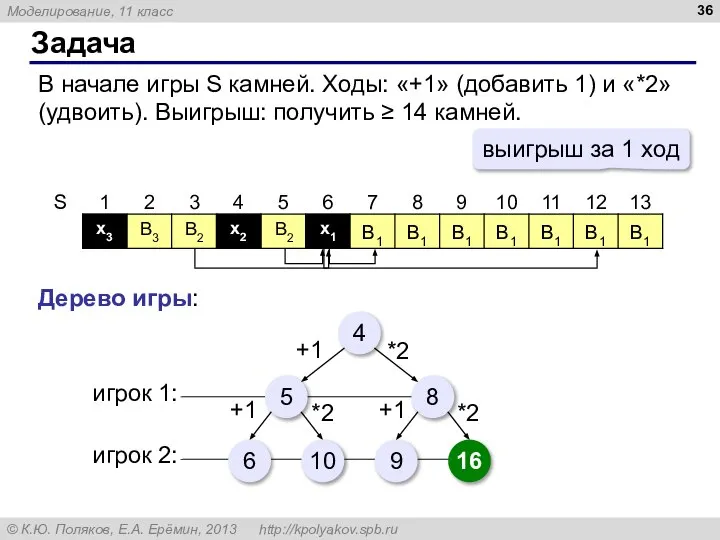
- 36. В2 x1 В2 x2 x3 В3 Задача В начале игры S камней. Ходы: «+1» (добавить 1)
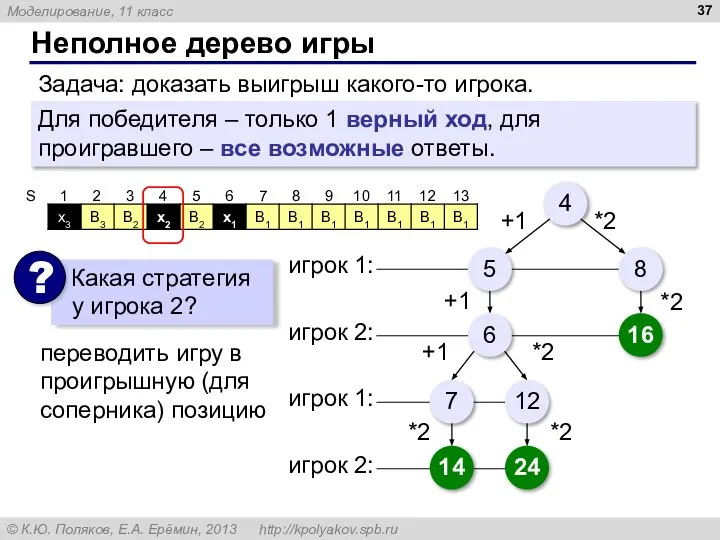
- 37. Неполное дерево игры Задача: доказать выигрыш какого-то игрока. Для победителя – только 1 верный ход, для
- 38. Задачи В начале игры S камней. Ходы: «+2» (добавить 2) и «*2» (удвоить). Выигрыш: получить ≥
- 39. Моделирование § 8. Этапы моделирования
- 40. I. Постановка задачи исследование оригинала изучение сущности объекта или явления анализ («что будет, если …») научиться
- 41. I. Постановка задачи Хорошо поставленная задача: описаны все связи между исходными данными и результатом известны все
- 42. I. Постановка задачи (пример) Спортсмен Вася в синей кепке бросает белый мяч со скоростью 12 м/с.
- 43. II. Разработка модели Спортсмен Вася в синей кепке бросает белый мяч со скоростью 12 м/с. Под
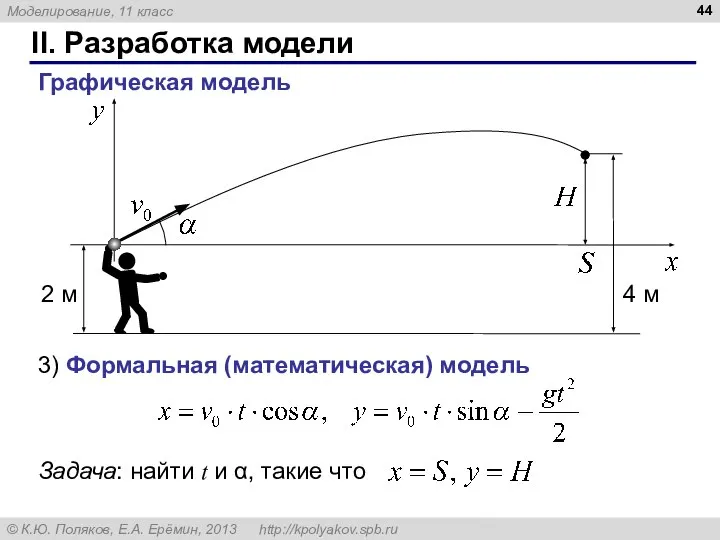
- 44. II. Разработка модели Графическая модель 3) Формальная (математическая) модель ,
- 45. Уточнение диапазона углов Диапазон углов для поиска:
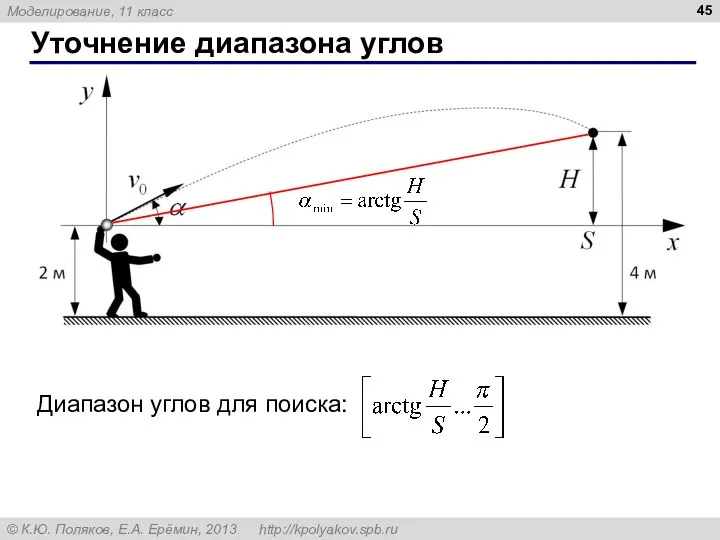
- 46. II. Разработка модели 4) Алгоритм моделирования Метод I. Меняем угол α. Для выбранного угла α строим
- 47. II. Разработка модели 5) Компьютерная модель программа (Паскаль, Си, …) электронные таблицы (Excel, OpenOffice.org Calc) среды
- 48. III. Тестирование модели Тестирование – это проверка модели на простых исходных данных с известным результатом. а)
- 49. IV. Эксперимент с моделью Эксперимент – это исследование модели при тех исходных данных, которые нас интересуют
- 50. V. Анализ результатов эксперимента Возможные выводы: задача решена, модель адекватна необходимо изменить алгоритм или условия моделирования
- 51. V. Анализ результатов всегда ли Вася сможет попасть в мишень? если начальная скорость отличается от заданной?
- 52. Моделирование § 9. Моделирование движения
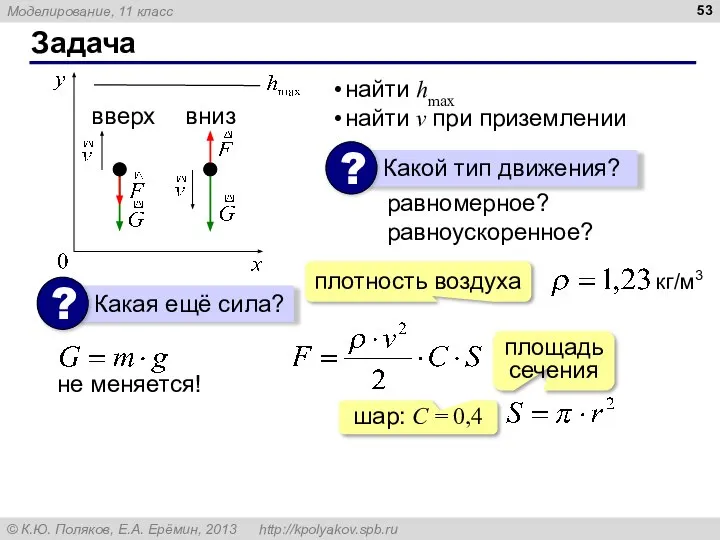
- 53. Задача найти hmax найти v при приземлении плотность воздуха площадь сечения шар: С = 0,4 равномерное?
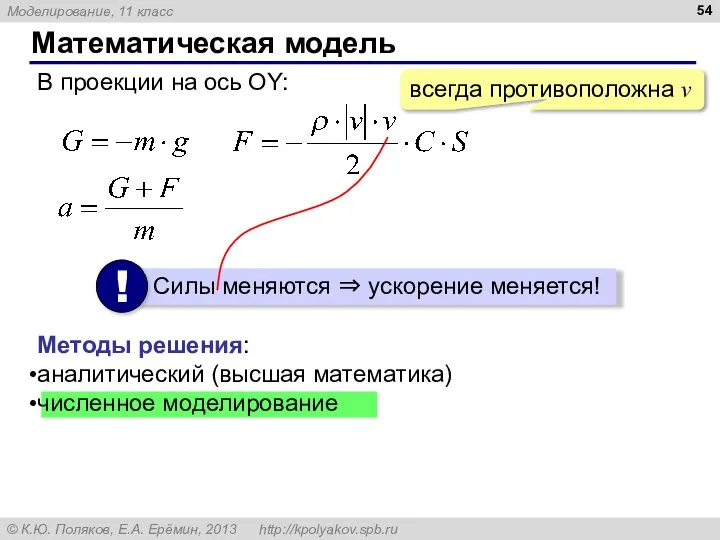
- 54. Математическая модель В проекции на ось OY: всегда противоположна v Методы решения: аналитический (высшая математика) численное
- 55. Дискретизация Дискретная модель описывает состояние системы при шаг дискретизации Задача: зная (yi, vi, ai) при ti
- 56. Компьютерная модель t:= 0; v:= v0; y:= 0 k:= ro*C*S/2 нц пока y >= 0 F:=
- 57. Моделирование § 10. Математические модели в биологии
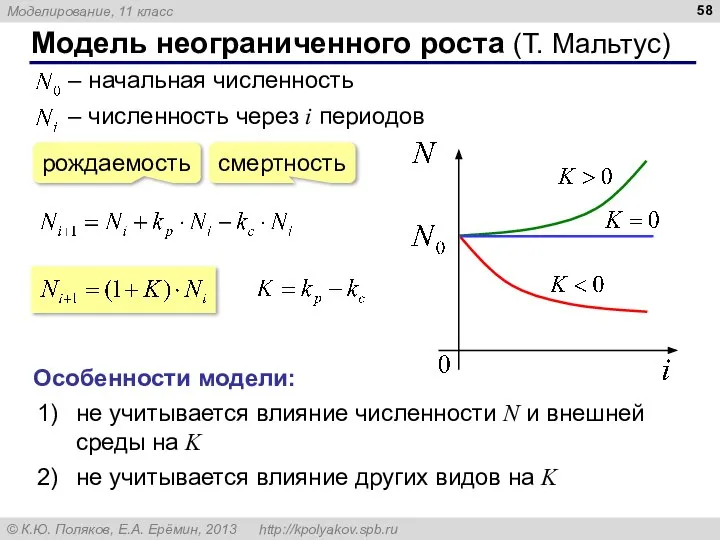
- 58. Модель неограниченного роста (Т. Мальтус) Особенности модели: не учитывается влияние численности N и внешней среды на
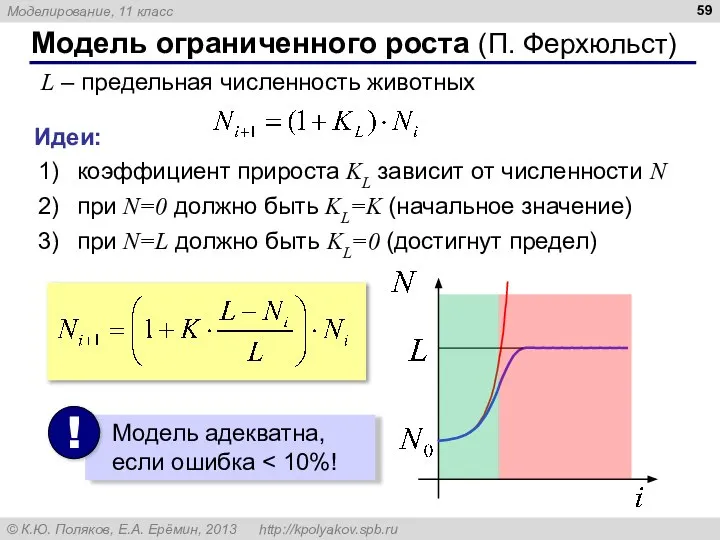
- 59. Модель ограниченного роста (П. Ферхюльст) L – предельная численность животных Идеи: коэффициент прироста KL зависит от
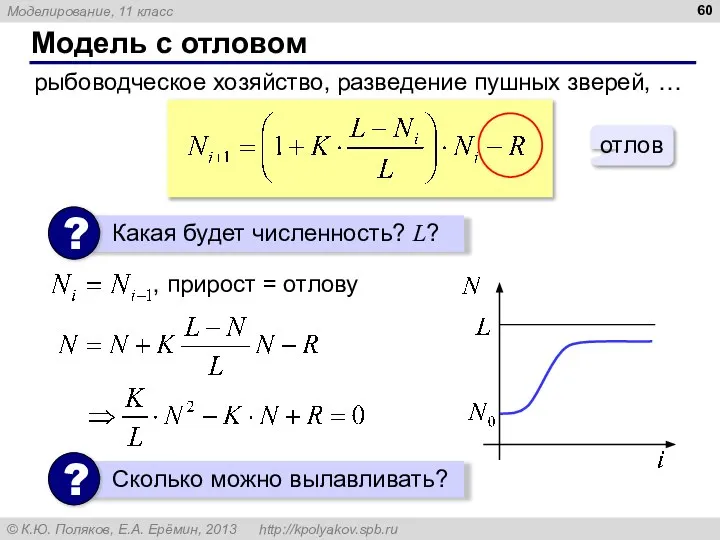
- 60. Модель с отловом рыбоводческое хозяйство, разведение пушных зверей, …
- 61. Модель «хищник-жертва» Модель – не-система: Модель – система: число встреч пропорционально Ni⋅Zi «эффект» пропорционален числу встреч
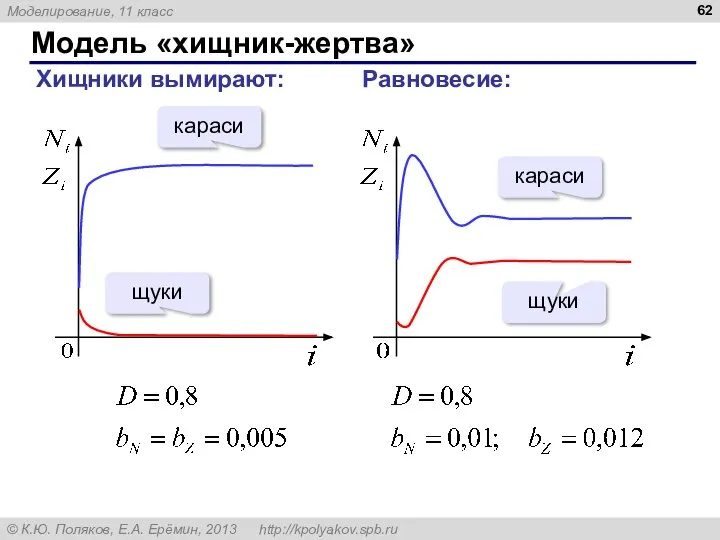
- 62. Модель «хищник-жертва» Хищники вымирают: Равновесие: караси щуки караси щуки
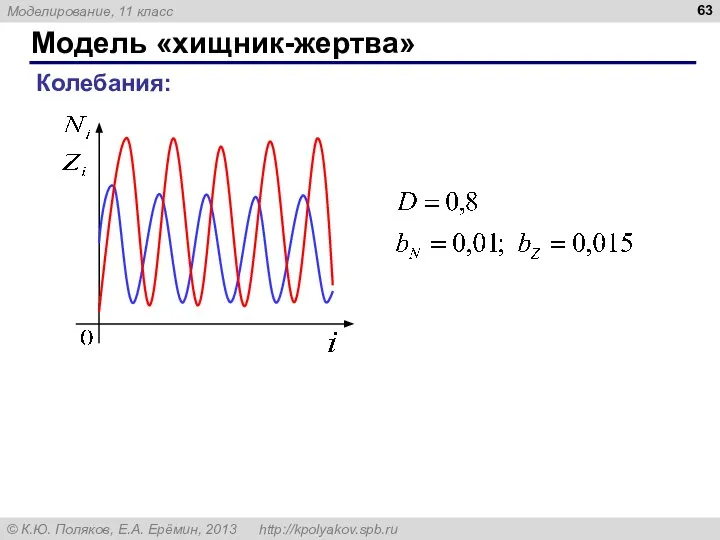
- 63. Модель «хищник-жертва» Колебания:
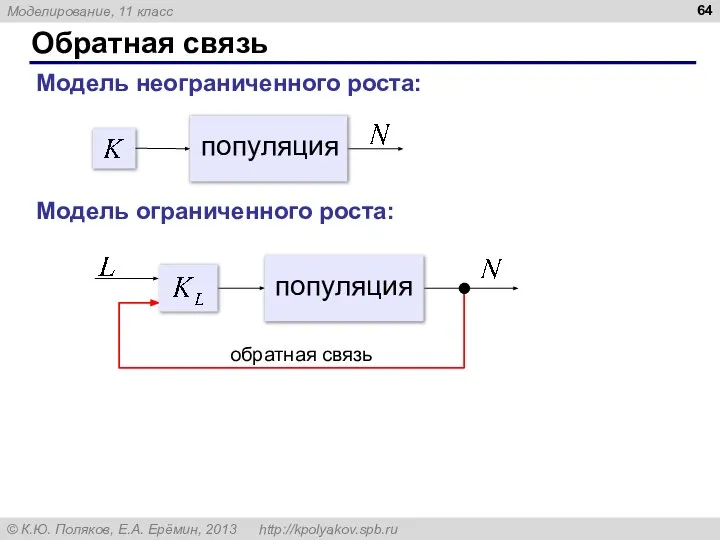
- 64. Обратная связь Модель неограниченного роста: Модель ограниченного роста:
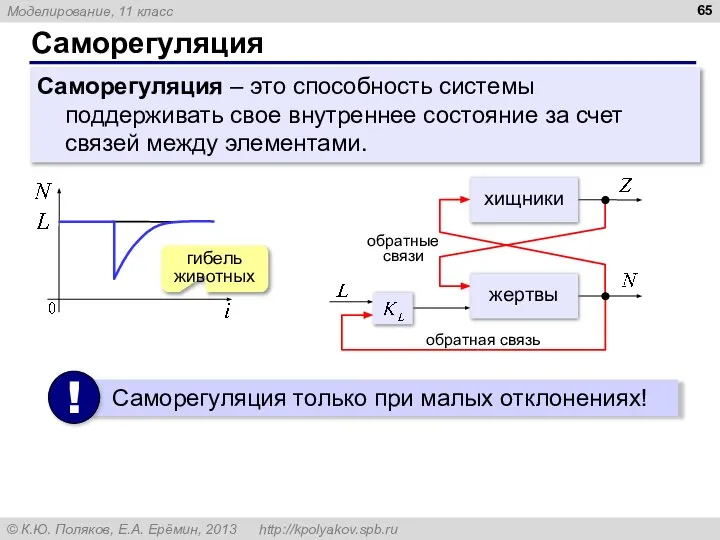
- 65. Саморегуляция Саморегуляция – это способность системы поддерживать свое внутреннее состояние за счет связей между элементами.
- 66. Моделирование § 11. Системы массового обслуживания
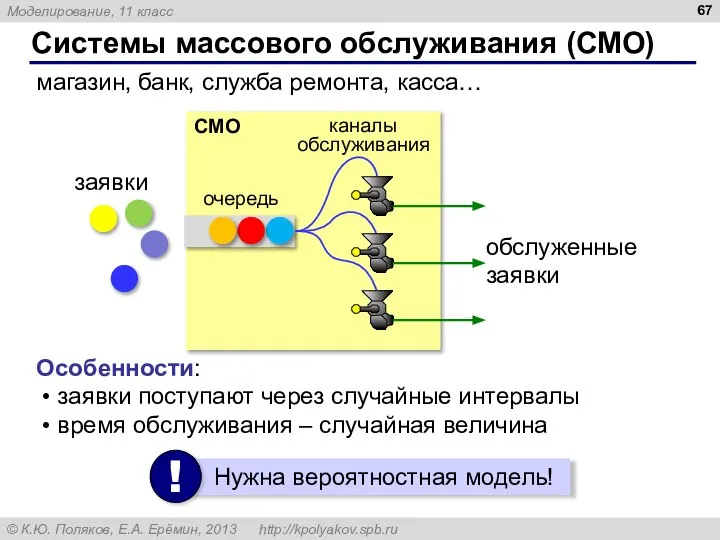
- 67. Системы массового обслуживания (СМО) магазин, банк, служба ремонта, касса… обслуженные заявки заявки поступают через случайные интервалы
- 68. Модель работы банка за 1 минуту входит P клиентов время обслуживания T минут K – количество
- 69. Модель работы банка K касс работают с одинаковой скоростью, но эта скорость меняется каждый интервал Ti
- 70. Модель работы банка K:= 2 | меняем количество касс Pmax:= 4 | макс. число входящих за
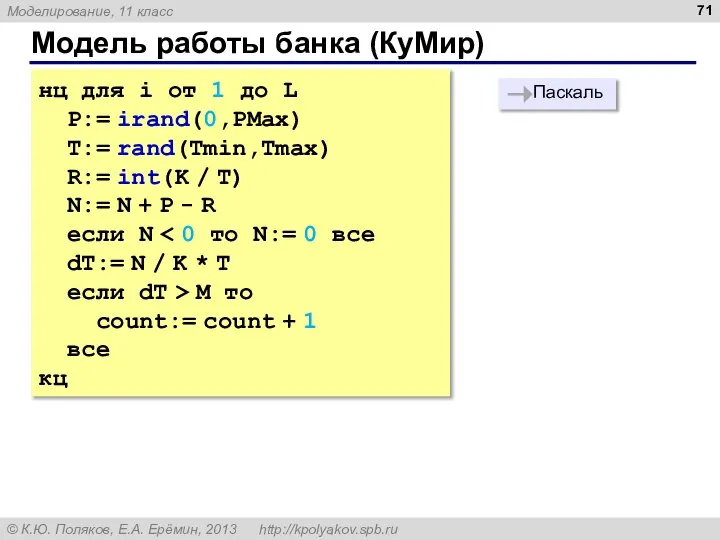
- 71. Модель работы банка (КуМир) нц для i от 1 до L P:= irand(0,PMax) T:= rand(Tmin,Tmax) R:=
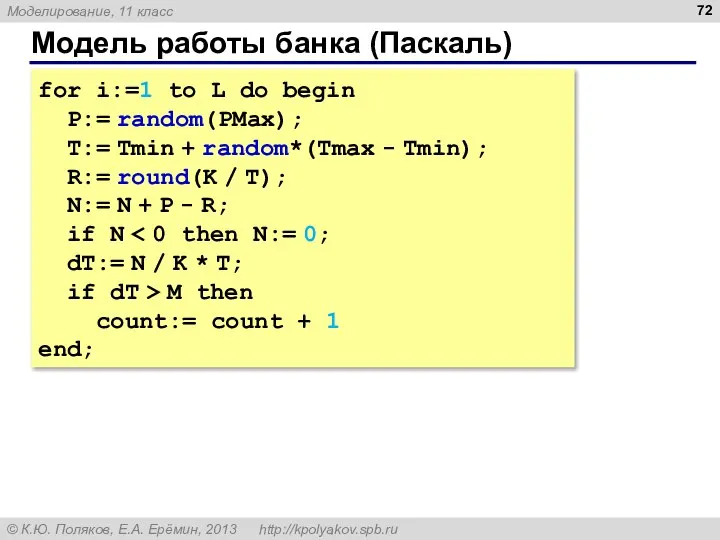
- 72. Модель работы банка (Паскаль) for i:=1 to L do begin P:= random(PMax); T:= Tmin + random*(Tmax
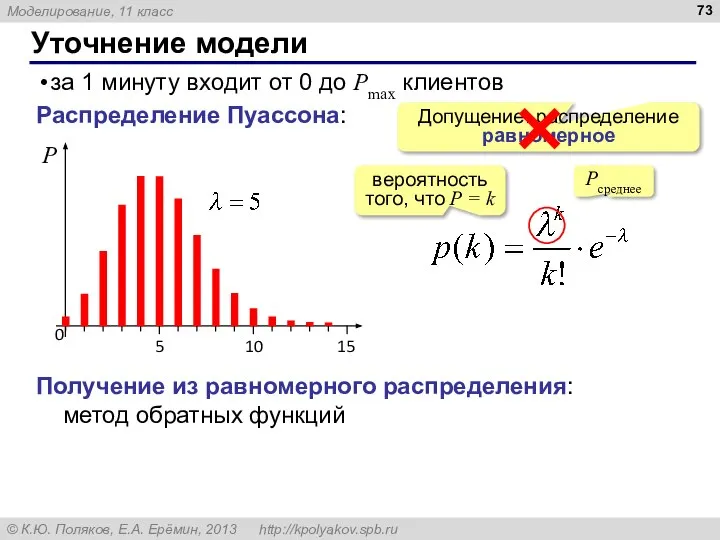
- 73. Уточнение модели за 1 минуту входит от 0 до Pmax клиентов Допущение: распределение равномерное Распределение Пуассона:
- 74. Распределение Пуассона (КуМир) алг цел Poisson(цел Lam) нач вещ s, r, alpha; цел k r:= exp(-Lam);
- 75. Распределение Пуассона (Паскаль) function Poisson(Lam: integer): integer; var s, r, alpha: real; k: integer; begin r:=
- 76. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 78. Скачать презентацию



































 Лабораторная работа. Изучение основ работы с Power Point. Информатика и системы счисления
Лабораторная работа. Изучение основ работы с Power Point. Информатика и системы счисления Создание канала
Создание канала Базы данных. Пример
Базы данных. Пример Простейшие коллективные операции передачи данных. Режимы передачи сообщений
Простейшие коллективные операции передачи данных. Режимы передачи сообщений Техника презентации
Техника презентации Предложения GROUP BY и HAVING
Предложения GROUP BY и HAVING Введение в теорию алгоритмов
Введение в теорию алгоритмов Мобильная версия
Мобильная версия Кто владеет информацией - тот владеет миром
Кто владеет информацией - тот владеет миром Структурированные типы данных. Двумерные массивы. Матрицы
Структурированные типы данных. Двумерные массивы. Матрицы Блочная модель
Блочная модель Вычислительная сложность. Базовые структуры данных и их использование в С++
Вычислительная сложность. Базовые структуры данных и их использование в С++ Создание информации с помощью интернет-сервисов
Создание информации с помощью интернет-сервисов Книга Дизайн логотипа. Боб Паташник
Книга Дизайн логотипа. Боб Паташник Игра в имитацию. Симметричное и асимметричное шифрование
Игра в имитацию. Симметричное и асимметричное шифрование Реализация алгоритмов в среде программирования. Часть 2. Программирование на VBA
Реализация алгоритмов в среде программирования. Часть 2. Программирование на VBA Пример админ панели
Пример админ панели Устройство компьютера
Устройство компьютера Презентация на тему Создание презентаций
Презентация на тему Создание презентаций  Применение триггера в презентациях Power Point
Применение триггера в презентациях Power Point Интеллектуальные системы защиты информации
Интеллектуальные системы защиты информации Отчет о ведении сообществ в социальных медиа
Отчет о ведении сообществ в социальных медиа История развития искусственных нейронных сетей
История развития искусственных нейронных сетей Знакомство с САПР. Аскон Компас
Знакомство с САПР. Аскон Компас Трассировка программ обработки массива
Трассировка программ обработки массива Угрозы безопасности и методы защиты информации в общественных организациях
Угрозы безопасности и методы защиты информации в общественных организациях Image resnet 34
Image resnet 34 Формула. Набор символов, написанный по специальным правилам и используемый для расчетов
Формула. Набор символов, написанный по специальным правилам и используемый для расчетов