Слайд 2Методы
Изменение способа определения шага
Изменение способа вычисления Δω

Слайд 3Изменение способа определения шага
Определять скорость обучения отдельно для каждого элемента W.
Изменять скорость

обучения для каждой итерации.
Если производная функции стоимости имеет постоянный знак для нескольких итераций, то скорость обучения растет
Если производная функции стоимости показывает изменение знак для нескольких итераций, то скорость обучения растет
Вносить импульсные вариации в скорость обучения.
Слайд 4Изменение способа вычисления Δω
Градиентный спуск
Методы сопряженных градиентов.
Квази-Ньютоновские методы.
Метод стохастиеского градиента

Слайд 5Градиентный спуск
Вектор частных производных функции
Задает направление наискорейшего возрастания этой функции

Слайд 6Метод сопряженных градиентов
Задача минимизации квадратичной функции.
Функцию стоимости аппроксимируем квадратичной функцией
f(w)=1/2 WT H

W - ∂Eav(W)/∂W W + c
В качестве направления наискорейшего спуска выбираем резидуальную ошибку r(n) – ошибка нахождения минимума
Не использует Гессиан, но его приближение
Слайд 7Нелинейный алгоритм сопряжен градиентов
Инициализация
Вычисления
W(0) по ВР находим градиент g(0)
S(0)=r(0)=-g(0) (r(0) – резидуальная

ошибка)
Для шага n - линейный поиск параметра η(n)
Находится группа (которая является нетривиальным интервалом), гарантированно содержащая минимум.
Разделение на подгруппы меньшего размера
Слайд 8Нелинейный алгоритм сопряжен градиентов
Ошибка r(n)W(n+1)=W(n)+ η(n)

s(n)
По ВР находим g(n+1)
r(n+1)=- g(n+1)
Вычисляем b по Полаку-Рибьеру
b(n+1)=max{0, (rT(n+1)(r(n+1)- r(n)))/(rT(n) r(n))}
Изменяем значение направления
s(n+1)=r(n+1)+b(n+1) s(n)
n=n+1 и к 3.
Слайд 9Метод Ньютона
Формула ньютона
Гессиан функции ошибки

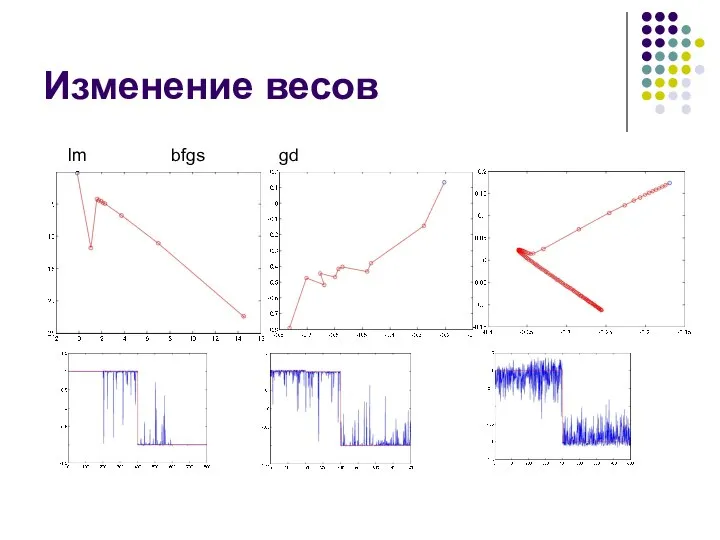
Слайд 10LM
ΔW= -(JT J +I*M)-1 JT E
H ≈ JT J
J- Якобиан
g= JT E

Слайд 11BFGS
ΔW= - H-1g(n)
s(n)P(n)=-g(n)
s(n)=s(n-1)+u(n)
V(n)=W(n+1)-W(n)
Y(n)=g(n+1)-g(n)
S(n+1)V(n)=Y(n)
Broyden-Fletcher-Goldfarb-Shano
P(n+1)=-g(n) +[(V(n)* g(n+1))*s(n)/(Y(n)*s(n))]
![BFGS ΔW= - H-1g(n) s(n)P(n)=-g(n) s(n)=s(n-1)+u(n) V(n)=W(n+1)-W(n) Y(n)=g(n+1)-g(n) S(n+1)V(n)=Y(n) Broyden-Fletcher-Goldfarb-Shano P(n+1)=-g(n) +[(V(n)* g(n+1))*s(n)/(Y(n)*s(n))]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1044697/slide-10.jpg)
Слайд 12Стохастический градиентный спуск
SGD (Stochastic Gradient Descent)
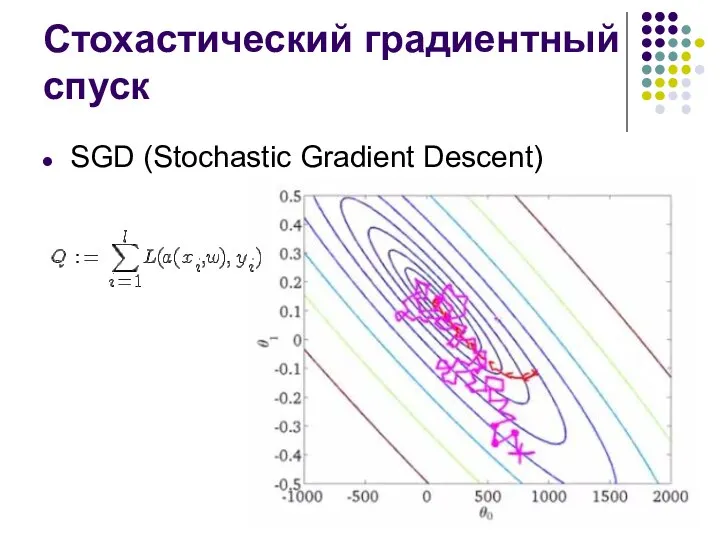
Слайд 13Стохастический градиентный спуск
Текущий шаг
Выбрать объект xi из (например, случайным образом);
Вычислить выходное значение алгоритма и ошибку;
Сделать шаг

градиентного спуска;
Оценить значение функционала;
Пока значение не стабилизируется и/или веса не перестанут изменяться.









![BFGS ΔW= - H-1g(n) s(n)P(n)=-g(n) s(n)=s(n-1)+u(n) V(n)=W(n+1)-W(n) Y(n)=g(n+1)-g(n) S(n+1)V(n)=Y(n) Broyden-Fletcher-Goldfarb-Shano P(n+1)=-g(n) +[(V(n)* g(n+1))*s(n)/(Y(n)*s(n))]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1044697/slide-10.jpg)


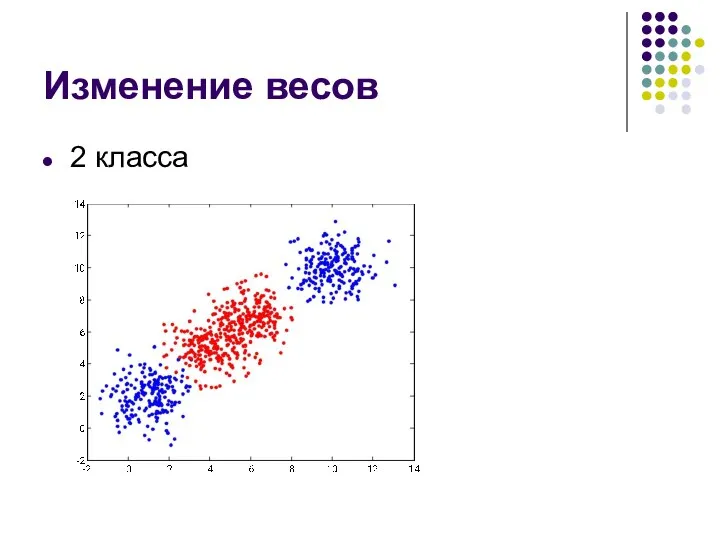
 WEB 3.0
WEB 3.0 Программирование на языке PascalABC. Решение задач. Обмен значений
Программирование на языке PascalABC. Решение задач. Обмен значений Инициализация жесткого диска
Инициализация жесткого диска Школа для развития своего таланта. Проект
Школа для развития своего таланта. Проект Систематизация сбора и оценки работ учащихся
Систематизация сбора и оценки работ учащихся Winbox 1
Winbox 1 Разработка веб-приложения для автоматизации обработки данных тестирования учащихся
Разработка веб-приложения для автоматизации обработки данных тестирования учащихся Telegram-канал Табуретка
Telegram-канал Табуретка Знакомство с программой PowerPoint
Знакомство с программой PowerPoint Стилевое оформление текста
Стилевое оформление текста Amadeus Property Management System - крупнейшая дистрибьюторская система
Amadeus Property Management System - крупнейшая дистрибьюторская система Как стать самозанятым?
Как стать самозанятым? Машинное обучение на языке программирования Python
Машинное обучение на языке программирования Python Электронные ресурсы Вологодской ОУНБ в помощь генеалогическому поиску
Электронные ресурсы Вологодской ОУНБ в помощь генеалогическому поиску Вычислительная практика. Интерфейс
Вычислительная практика. Интерфейс Шкідливі програми
Шкідливі програми Демоны (Программы) Linux
Демоны (Программы) Linux Обработка потока данных. Цикл с параметром
Обработка потока данных. Цикл с параметром Программирование ветвлений. Основы программирования
Программирование ветвлений. Основы программирования Создание рабочего стола
Создание рабочего стола Загальне завдання. Створення документа
Загальне завдання. Створення документа Регистрация на Портале РКЦ
Регистрация на Портале РКЦ Безопасность в сети Интернет
Безопасность в сети Интернет Установка VRay
Установка VRay поколения ЭВМ
поколения ЭВМ Этические основы общения в Сети Интернет
Этические основы общения в Сети Интернет ЯПВУ. Лекция 1. Виды интерфейсов Windows
ЯПВУ. Лекция 1. Виды интерфейсов Windows іт гр 32 урок 2
іт гр 32 урок 2