Различные подходы к измерению количества информации

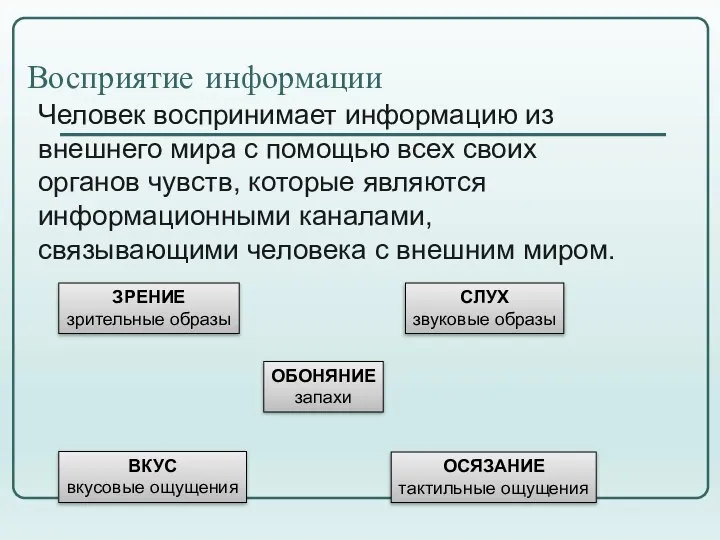
Восприятие информации
Человек воспринимает информацию из внешнего мира с помощью всех своих органов чувств, которые являются информационными каналами, связывающими человека с внешним миром.
ЗРЕНИЕ
зрительные образы
ОБОНЯНИЕ
запахи
ВКУС
вкусовые ощущения
СЛУХ
звуковые образы
ОСЯЗАНИЕ
тактильные ощущения

Виды информации
По способу восприятия:
Визуальная
Аудиальная
Тактильная
Вкусовая
обонятельная

Виды информации
По форме представления:
Графическая
Числовая
Текстовая
Звуковая
Табличная

Существуют различные подходы к измерению количества информации:
1) Алфавитный
2) Содержательный
3) Вероятностный
Количество информации – это числовая характеристика информации, отражающая ту степень неопределенности, которая исчезает после получения информации.

1. АЛФАВИТНЫЙ ПОДХОД
Алфавитный подход основан на подсчете числа символов в сообщении и позволяет определить количество информации, заключенной в тексте. При алфавитном подходе, определяется количество информации без учета содержания и рассматривают информационное сообщение как последовательность знаков определенной знаковой системы.
Алфавитный подход является объективным, т.е. он не зависит от субъекта (человека), воспринимающего текст.
Данный подход удобен при использовании технических средств работы с информацией, т.к. не учитывается содержание сообщения.

Основоположником алфавитного подхода измерения информации является великий российский ученый-математик Андрей Николаевич Колмогоров (1903-1987).

Обычно под алфавитом понимают только буквы, но поскольку в тексте могут встречаться знаки препинания, цифры, скобки, пробел, то они могут включатся в алфавит, если это оговорено в условии задачи.
Ограничений на максимальную (max) мощность алфавита нет, но есть достаточный алфавит мощностью 256 символов. Этот алфавит используется для представления текстов в компьютере.
Поскольку 256=28, то 1символ несет в тексте 8 бит информации.
АЛФАВИТ – это вся совокупность символов, используемых в некотором языке для представления информации.
Алфавитный подход – как способ измерения информации.

При алфавитном подходе считается, что каждый символ текста имеет определенный «информационный вес». Информационный вес символа зависит от мощности алфавита и обозначается i.
Алфавит, который содержит наименьшее число символов, используется в компьютере. Он содержит всего два символа 0 и 1 и называется двоичным алфавитом.
Информационный вес символа двоичного алфавита принят за единицу информации и называется 1 бит.
Например, чтобы посчитать количество информации в следующем двоичном тексте 110011111100101000101011, нужно пересчитать все 0 и 1.
В тексте содержится 24 бита информации.

При алфавитном подходе к измерению информации количество информации зависит не от содержания, а от размера текста и мощности алфавита.
МОЩНОСТЬ АЛФАВИТА (N) – это полное число символов в алфавите.
Например,
1) мощность русского алфавита составляет N=33;
2) мощность английского алфавита N= ?

3) алфавит десятичной системы счисления – это множество цифр- 0,1,2,3,4,5,6,7,8,9.
Мощность такого алфавита N=10.
4) Компьютерный алфавит, используемый для представления текстов в компьютере, использует 256 символов, т.е. N=256
5) Алфавит двоичной системы кодирования информации имеет всего два символа-
0 и 1, поэтому N=2.
Замечание. С увеличением мощности алфавита увеличивается информационный вес символов этого алфавита.

МОЩНОСТЬ АЛФАВИТА
число символов в алфавите (его размер)
N
ИНФОРМАЦИОННЫЙ ВЕС СИМВОЛА
количество информации в одном символе
I = K ∙ i
i
2 i = N
Информационный вес каждого символа (i) и
мощность алфавита (N) связаны формулой:
Количество (объем) информации в сообщении (I) можно посчитать по формуле:
Количество информации в сообщении или информационный объём текста (I), равен количеству информации, которое несет один символ (i), умноженное на количество символов K в сообщении, т.е. I = K ∙ i

Измерение информации
Вся информация, обрабатываемая компьютером, представлена двоичным кодом с помощью двух цифр – 0 и 1.
Эти два символа 0 и 1 принято называть битами
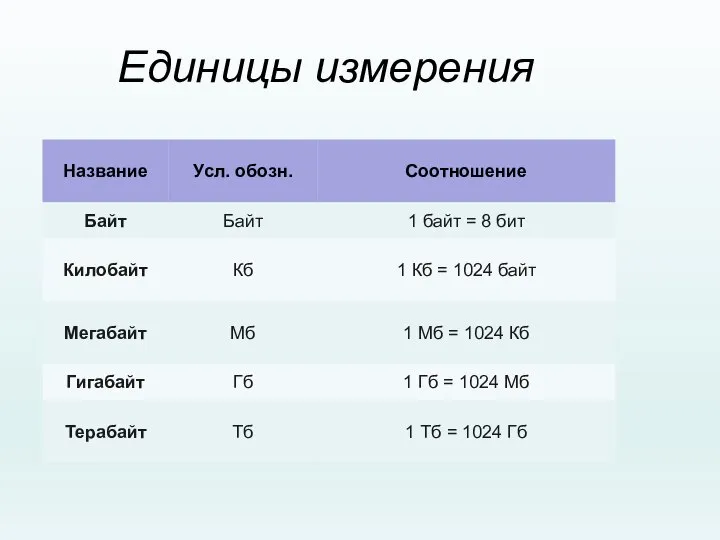
Бит – наименьшая единица измерения объема информации.

Единицы измерения

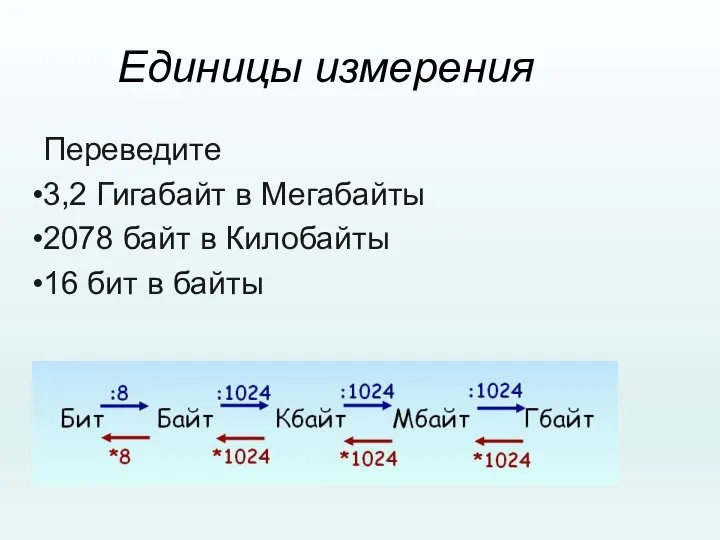
Единицы измерения
Переведите
3,2 Гигабайт в Мегабайты
2078 байт в Килобайты
16 бит в байты

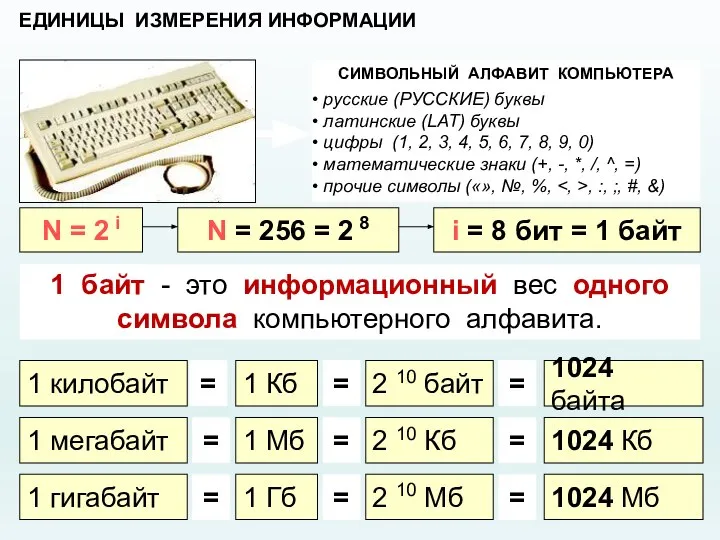
ЕДИНИЦЫ ИЗМЕРЕНИЯ ИНФОРМАЦИИ
СИМВОЛЬНЫЙ АЛФАВИТ КОМПЬЮТЕРА
русские (РУССКИЕ) буквы
латинские (LAT) буквы
цифры (1, 2, 3, 4, 5, 6, 7, 8, 9, 0)
математические знаки (+, -, *, /, ^, =)
прочие символы («», №, %, <, >, :, ;, #, &)
1 байт - это информационный вес одного символа компьютерного алфавита.

Скорость передачи информации
Прием-передача информации могут происходить с разной скоростью.
Количество информации, передаваемое за единицу времени, есть скорость передачи информации или скорость информационного потока.
Единицы измерения скорости передачи информации: бит в секунду (бит/с), байт в секунду (байт/с), килобайт в секунду (Кбайт/с) и т.д.

Пример 1. Подсчитайте объем информации, содержащейся в романе А. Дюма "Три мушкетера", и определите, сколько близких по объему книг можно разместить на одном лазерном диске емкостью 600 Мбайт? (в книге 590 стр., 48 строк на одной странице, 53 символа в строке).
Решение.
590*48*53=1500960(символов).
Информационный вес одного символа, по определению, составляет 1 байт, тогда:
1500960байт=1466Кбайт= 1,4Мбайт.
3) На одном лазерном диске емкостью 600 Мбайт можно разместить 600 : 1,4 = 428, 57, т.е около 428 произведений, близких по объему к роману А. Дюма "Три мушкетера".
Ответ: I = 1,4 Мб; 428 книг.

Пример 2. На диске объемом 100 Мбайт подготовлена к выдаче на экран дисплея информация: 24 строчки по 80 символов, эта информация заполняет экран целиком. Какую часть диска она занимает?
Решение.
К = 24*80=1920 (символов)
Т.к. информационный вес одного символа компьютерного алфавита составляет 1 байт, то I = 1920 байт.
Объем диска 100*1024*1024 байт = 104857600 байт
1920/104857600=0,000018 (часть диска).
Ответ: 0,000018 часть диска.

Домашнее задание.
ЗАДАЧА 1
Книга, подготовленная с помощью компьютера, содержит 150 страниц. На каждой странице – 40 строк, в каждой строке – 60 символов (включая пробелы между словами). Каков объем информации в книге?
ЗАДАЧА 2
Текст составлен с помощью алфавита мощностью в 64 символа и содержит 100 символов. Каков информационный объем текста.
ЗАДАЧА 3
Сообщение записано буквами из 16 символьного алфавита, содержит 50 символов. Какой объем информации оно несет.
ЗАДАЧА 4
Два текста содержат одинаковое количество символов. Первый текст составлен в алфавите мощностью 32 символа, второй – мощностью 64 символа. Во сколько раз отличатся количество информации в этих текстах.

2. СОДЕРЖАТЕЛЬНЫЙ ПОДХОД
(количество информации зависит от ее содержания)
Основоположником этого подхода является американский учёный Клод Элвуд Шеннон(1916 — 2001).
По Шеннону, информация — это мера уменьшения неопределенности наших знаний.
Неопределенность некоторого события — это количество возможных исходов данного события.

Информация — это знания людей, получаемые ими из различных сообщений.
Сообщение — это информационный поток (поток данных), который в процессе передачи информации поступает к принимающему его субъекту.
Сообщение
Информативное, если оно пополняет знания человека, т.е. несет для него информацию.
Количество информации в информативном сообщении больше нуля.
Неинформативное, если это:
«старые» сведения, т.е. человек это уже знает;
содержание сообщения непонятно человеку.
Количество информации в неинформативном сообщении равно нулю.

Вероятность некоторого события — это величина, которая может принимать значения от нуля до единицы.
Вероятность некоторого события определяется путем многократных наблюдений (измерений, испытаний). Такие измерения называют статистическими. И чем большее количество измерений выполнено, тем точнее определяется вероятность события.
ОПРЕДЕЛЕНИЯ

Формула, используемая для вычисления количества информации, зависит от ситуаций, которых может быть две:
1. Все возможные варианты события равновероятны. Их число равно N.
2. Вероятности (p) возможных вариантов события разные и они заранее известны:
{pi }, i = 1..N.
Здесь по-прежнему N-число возможных вариантов события.

Равновероятные события.
2i = N
1 бит — это количество информации в сообщении об одном из двух равновероятных событий.
Формула Хартли — это показательное уравнение. Если i неизвестная величина, то решением данного уравнения будет:
i = log2N
Данные формулы тождественны друг другу.
События равновероятны, если ни одно из них не имеет преимущества перед другими.
Если обозначить буквой i количество информации в сообщении о том, что произошло одно из N равновероятных событий, то величины i и N связаны между собой формулой Хартли:

Примеры.
Пример 1. Сколько информации содержит сообщение о том, что из колоды карт достали даму пик?
Решение: В колоде 32 карты. В перемешанной колоде выпадение любой карты — равновероятные события. Если i — количество информации в сообщении о том, что выпала конкретная карта (например, дама пик), то из уравнения Хартли:
2i = 32 = 25
Ответ: i = 5 бит.

Пример 2. Сколько информации содержит сообщение о выпадении грани с числом 3 на шестигранном игральном кубике?
Решение. Считая выпадение любой грани событием равновероятным, запишем формулу Хартли:
2i = 6.
Ответ: i = log26 = 2,58496 бит.

Данную задачу можно решить иначе:
Из уравнения Хартли имеем: 2i = 6.
Так как 22 < 6 < 23, следовательно,
2 < i < 3.
Затем определяем более точное значение (с точностью до пяти знаков после запятой), что i = 2,58496 бит.
Замечание. При данном подходе к вычислению количества информации ответ будет выражен дробной величиной.

2i = 1/p
Решая данное показательное уравнение относительно i, получаем:
i = log2(1/p) формула Шеннона
3. Вероятностный подход
Осуществим при неравновероятных событиях.
Неравновероятные события – это события, имеющие разную вероятность реализации.
Если вероятность некоторого события равна p, а i (бит) — это количество информации в сообщении о том, что произошло это событие, то данные величины связаны между собой формулой:

Пример 3. На автобусной остановке останавливаются два маршрута автобусов: № 5 и № 7. Студенту дано задание: определить, сколько информации содержит сообщение о том, что к остановке подошел автобус № 5, и сколько информации в сообщении о том, что подошел автобус № 7.

Решение. Студент провел исследование. В течение всего рабочего дня он подсчитал, что к остановке автобусы подходили 100 раз. Из них — 25 раз подходил автобус № 5 и 75 раз подходил автобус № 7. Сделав предположение, что с такой же частотой автобусы ходят и в другие дни, ученик вычислил вероятность появления на остановке автобуса № 5: p5 = 25/100 = 1/4, и вероятность появления автобуса № 7:
p7 = 75/100 = 3/4.
Отсюда, количество информации в сообщении об автобусе № 5 равно: i5 = log24 = 2 бита. Количество информации в сообщении об автобусе № 7 равно:
i7 = log2(4/3) = log24 – log23 = 2 – 1,58496 = 0,41504 бита.
Ответ: i5 = 2 бита; i7 = 0,41504 бита.

Пример 4. Рассмотрим другой вариант задачи об автобусах. На остановке останавливаются автобусы № 5 и № 7. Сообщение о том, что к остановке подошел автобус № 5, несет 4 бита информации. Вероятность появления на остановке автобуса с № 7 в два раза меньше, чем вероятность появления автобуса № 5. Сколько бит информации несет сообщение о появлении на остановке автобуса № 7?
Решение. i5 = 4 бита, p5 = 2 · p7
Вспомним связь между вероятностью и количеством информации: 2i = 1/p
Отсюда: p = 2–i
Подставляя в равенство из условия задачи, получим:
Отсюда:

Вывод: уменьшение вероятности события в 2 раза увеличивает информативность сообщения о нем на 1 бит.
Очевидно и обратное правило: увеличение вероятности события в 2 раза уменьшает информативность сообщения о нем на 1 бит. Зная эти правила, предыдущую задачу можно было решить «в уме».