Содержание
- 2. Машина Тьюринга – абстрактный исполнитель, осуществляющий алгоритмический процесс, созданный для уточнения понятия алгоритма. Это математический объект,
- 3. Структура и описание машины Тьюринга Машина Тьюринга состоит из: бесконечной ленты, разделенной на ячейки; каретки (читающей
- 4. 1) Внешний алфавит А = {a0, a1, …, an} Элемент a0 называется пустой символ или пустая
- 5. 2) Внутренний алфавит Q = {q0, q1, …, qm}, {П, Л, Н!} В любой момент времени
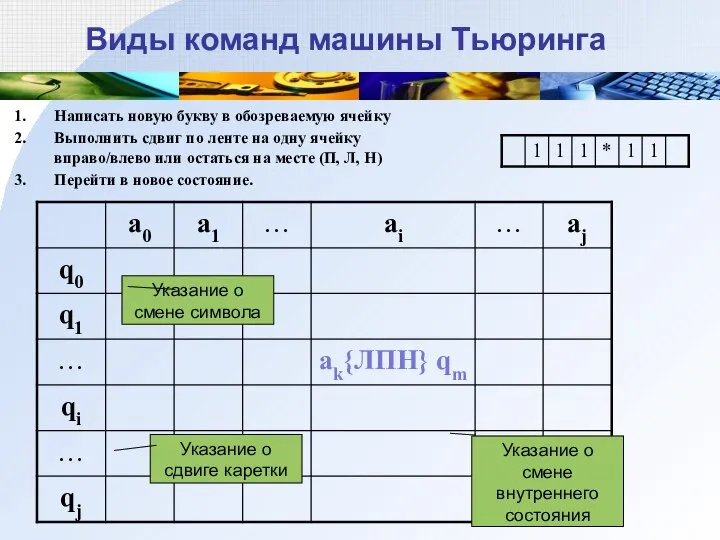
- 6. Виды команд машины Тьюринга Написать новую букву в обозреваемую ячейку Выполнить сдвиг по ленте на одну
- 7. 3) Внешняя память (лента) Машина имеет ленту, разбитую на ячейки, в каждую из которых может быть
- 8. 3) Внешняя память (лента) Устройство машины Тьюринга Пустая клетка содержит a0. В каждый момент времени на
- 9. 4) Каретка (управляющая головка) Каретка машины располагается над некоторой ячейкой ленты – воспринимает символ, записанный в
- 10. 5) Функциональная схема (программа) Программа машины состоит из команд: Устройство машины Тьюринга Для каждой пары (qi,
- 11. К началу работы машины на ленту подается исходный набор данных в виде слова α Описание работы
- 12. Описание работы машины Тьюринга Стандартное положение называется начальным (заключительным), если машина, воспринимающая слово в стандартном положении,
- 13. Находясь в не заключительном состоянии, машина совершает шаг, который определяется текущим состоянием qi и обозреваемым символом
- 14. Описание работы машины Тьюринга В соответствии с командой qiaj → qkal Х выполняются следующие действия: 1)
- 15. При переходе машины в заключительное состояние q0 ее работа прекращается На ленте записан результат работы алгоритма
- 16. Машинным словом (конфигурацией) машины Тьюринга называется слово вида α1qkal α2, где α1 и α2 - слова
- 17. Конфигурация α1qkal α2 интерпретируется следующим образом: - машина находится в состоянии qk - каретка обозревает на
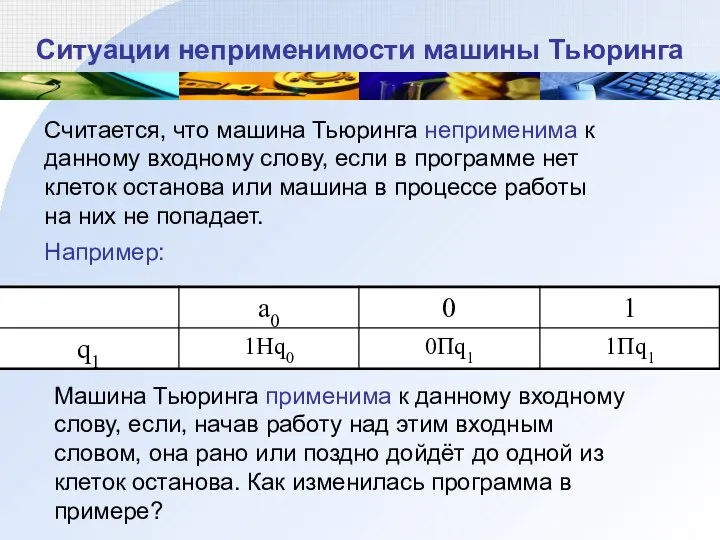
- 18. Ситуации неприменимости машины Тьюринга Считается, что машина Тьюринга неприменима к данному входному слову, если в программе
- 19. Пример машин Тьюринга Требуется построить машину Тьюринга для решения следующей задачи: во входном слове все буквы
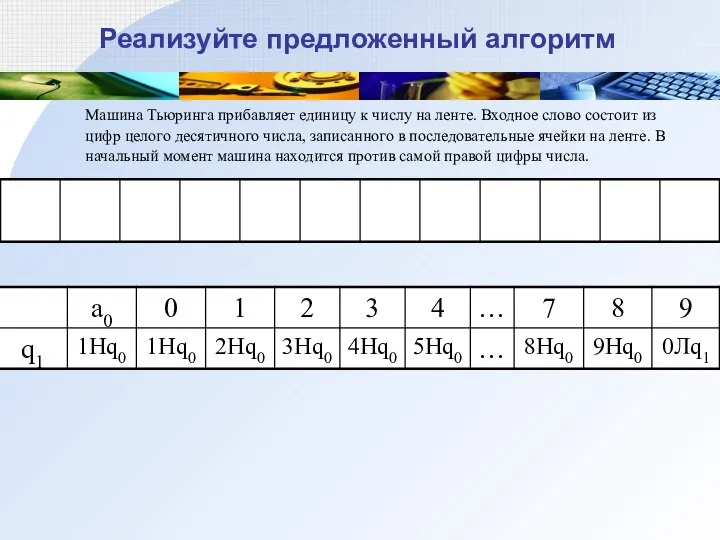
- 20. Реализуйте предложенный алгоритм Машина Тьюринга прибавляет единицу к числу на ленте. Входное слово состоит из цифр
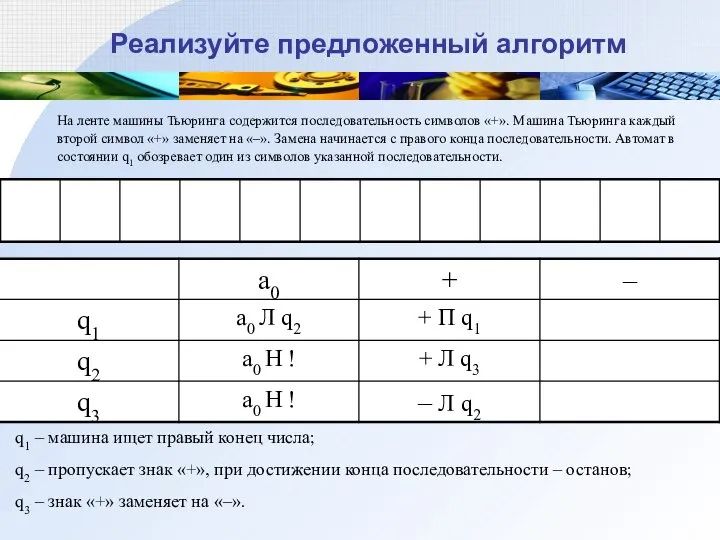
- 21. Реализуйте предложенный алгоритм На ленте машины Тьюринга содержится последовательность символов «+». Машина Тьюринга каждый второй символ
- 22. Пример Дана машина Тьюринга с внешним алфавитом А = {a0, 1, * }, алфавитом внутренних состояний
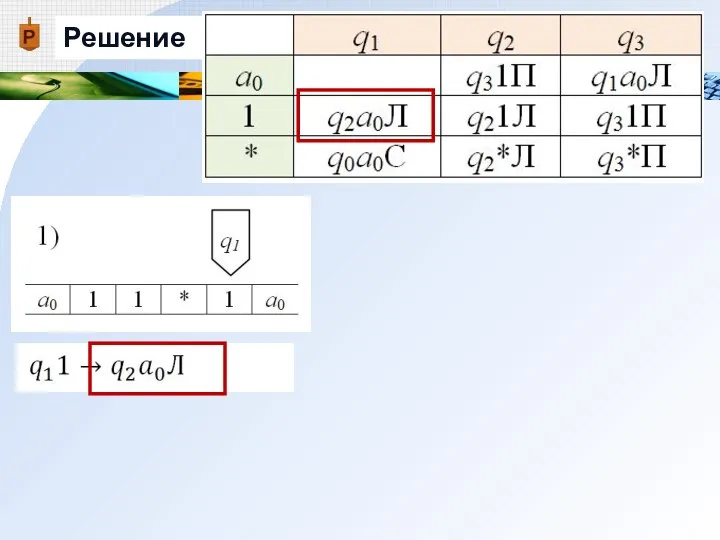
- 23. Решение
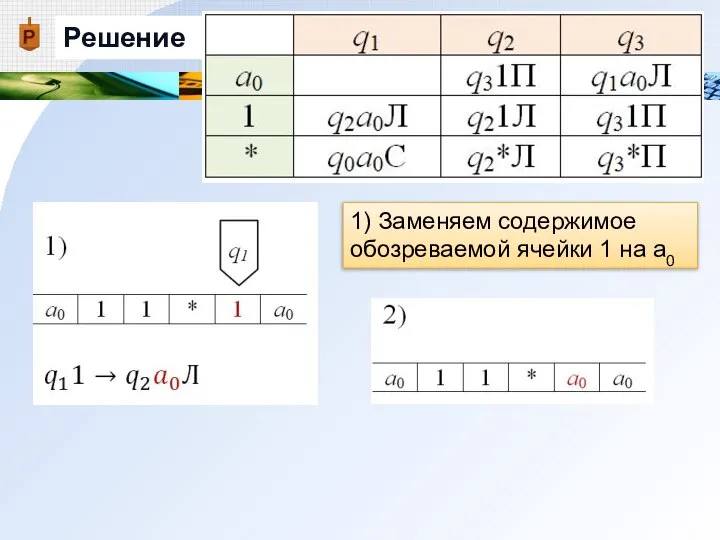
- 24. Решение 1) Заменяем содержимое обозреваемой ячейки 1 на а0
- 25. Решение 2) Машина переходит в новое состояние q2
- 26. Решение 3) Каретка перемещается влево
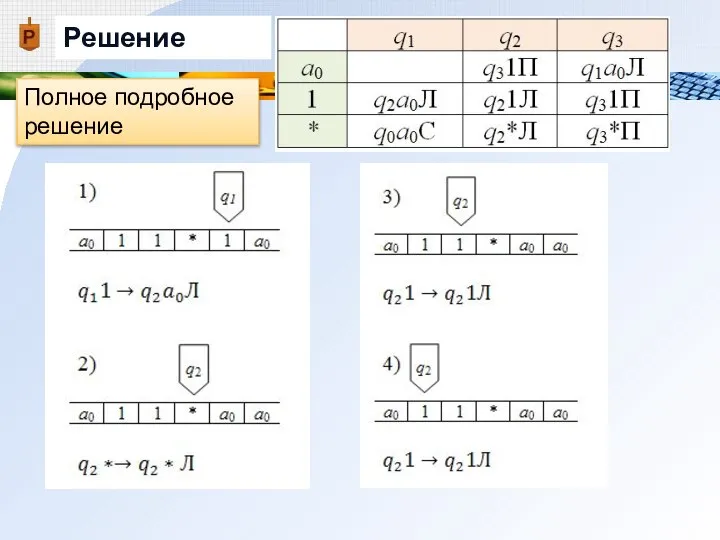
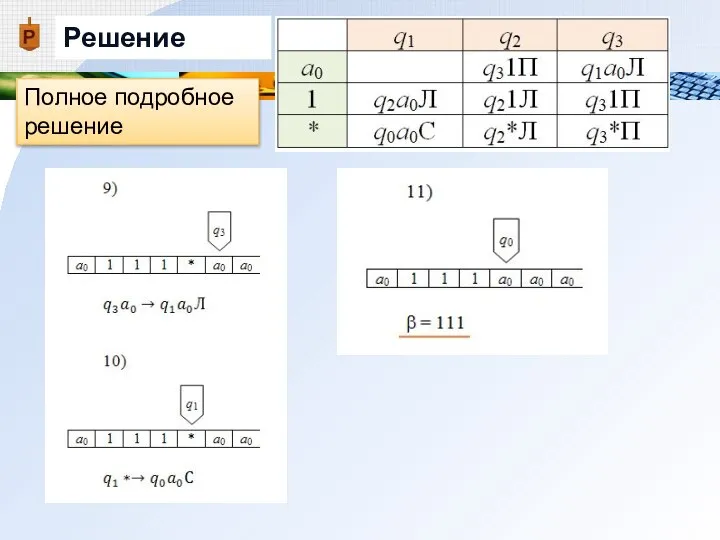
- 27. Решение Полное подробное решение
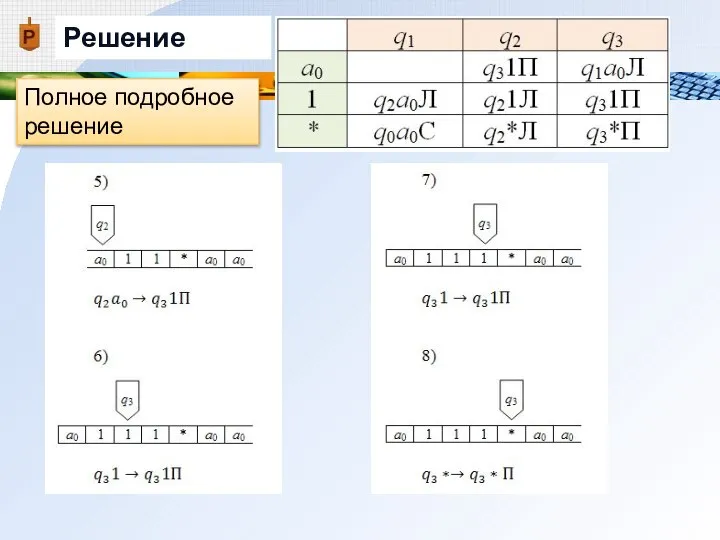
- 28. Решение Полное подробное решение
- 29. Решение Полное подробное решение
- 30. Решение Решение, записанное с помощью конфигураций (в строчку)
- 32. Скачать презентацию




















 Python. Циклы. Урок 4
Python. Циклы. Урок 4 Millionaire
Millionaire Школа::Кода Основы программирования на языке Python. 27 занятие
Школа::Кода Основы программирования на языке Python. 27 занятие REST in peace?
REST in peace? Как написать грамотный PR-текст для социальных сетей: практические советы с примерами
Как написать грамотный PR-текст для социальных сетей: практические советы с примерами Файлы и файловая структура
Файлы и файловая структура Коммутация каналов и пакетов кафедра ЮНЕСКО по НИТ
Коммутация каналов и пакетов кафедра ЮНЕСКО по НИТ Тема+5.+Переменные+и+операторы
Тема+5.+Переменные+и+операторы Обработка информации средствами математической логики
Обработка информации средствами математической логики Поддержка ЕАС ОПС – система Naumen
Поддержка ЕАС ОПС – система Naumen Заголовок слайда
Заголовок слайда Алгебра логики
Алгебра логики Двоичное кодирование
Двоичное кодирование Составные объекты: логические операции
Составные объекты: логические операции Перспективы продвижения ореха грецкого в Центральном Черноземье
Перспективы продвижения ореха грецкого в Центральном Черноземье ИК Базы данных. Урок 6. Презентация
ИК Базы данных. Урок 6. Презентация Программирование на языке Python. Алгоритм и его свойства
Программирование на языке Python. Алгоритм и его свойства ForService. Импорт в групповой прием
ForService. Импорт в групповой прием Основные понятия теории автоматического управления. Лекция 1
Основные понятия теории автоматического управления. Лекция 1 Решение алгоритмических задач с помощью электронных таблиц
Решение алгоритмических задач с помощью электронных таблиц Теория баз данных
Теория баз данных Файловая система компьютера
Файловая система компьютера Asymptotic Analysis
Asymptotic Analysis Понятие электронного документооборота
Понятие электронного документооборота Системное администрирование. Про unix
Системное администрирование. Про unix Информационно-библиотечный центр
Информационно-библиотечный центр Программирование в компьютерных системах
Программирование в компьютерных системах Выполнение и составление алгоритмов, содержащих ветвление
Выполнение и составление алгоритмов, содержащих ветвление