Оптимизатор Solver (встроен в Microsoft Excel)

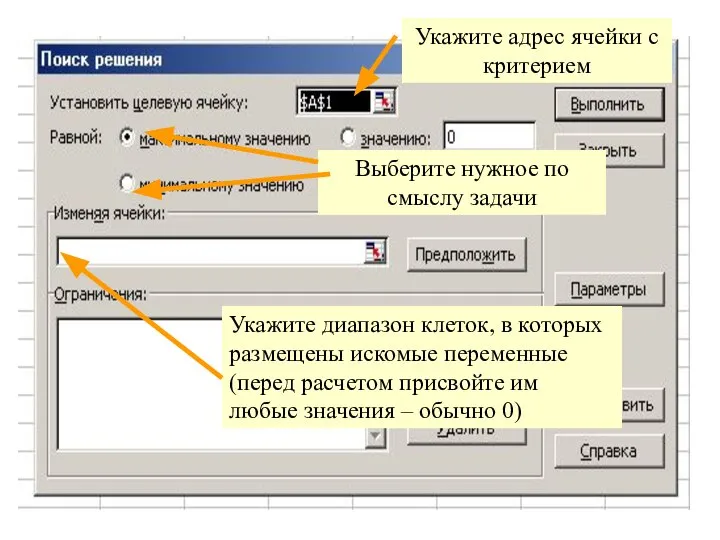
Укажите адрес ячейки с критерием
Выберите нужное по смыслу задачи
Укажите диапазон клеток, в которых
размещены искомые переменные
(перед расчетом присвойте им
любые значения – обычно 0)

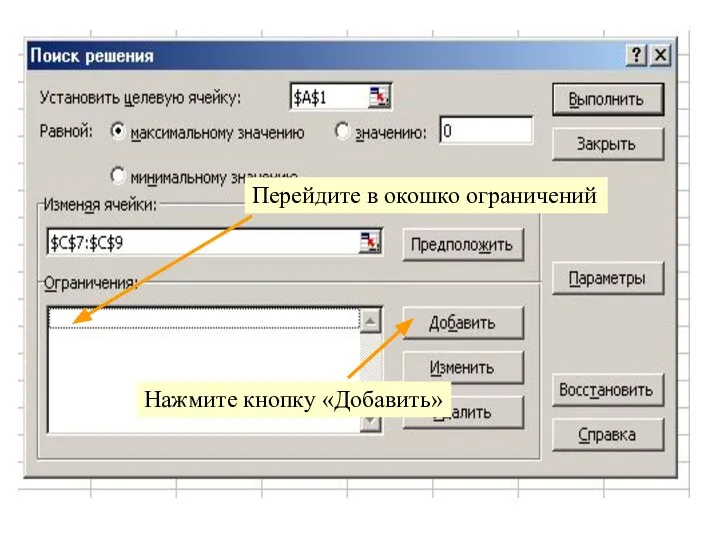
Перейдите в окошко ограничений
Нажмите кнопку «Добавить»

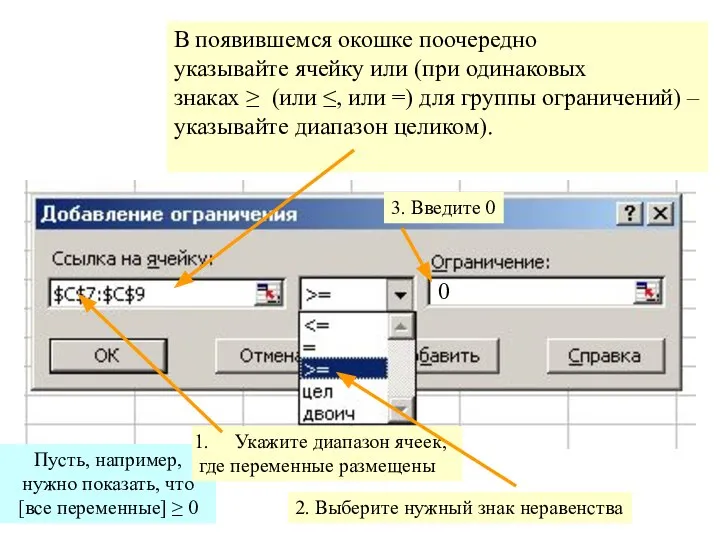
В появившемся окошке поочередно
указывайте ячейку или (при одинаковых
знаках ≥ (или ≤, или =) для группы ограничений) –
указывайте диапазон целиком).
Пусть, например, нужно показать, что [все переменные] ≥ 0
Укажите диапазон ячеек,
где переменные размещены
2. Выберите нужный знак неравенства
3. Введите 0
0

Последовательно введите все ограничения
(кнопка «Добавить»)
После ввода всех ограничений нажмите ОК
для возврата в основное окно Solver

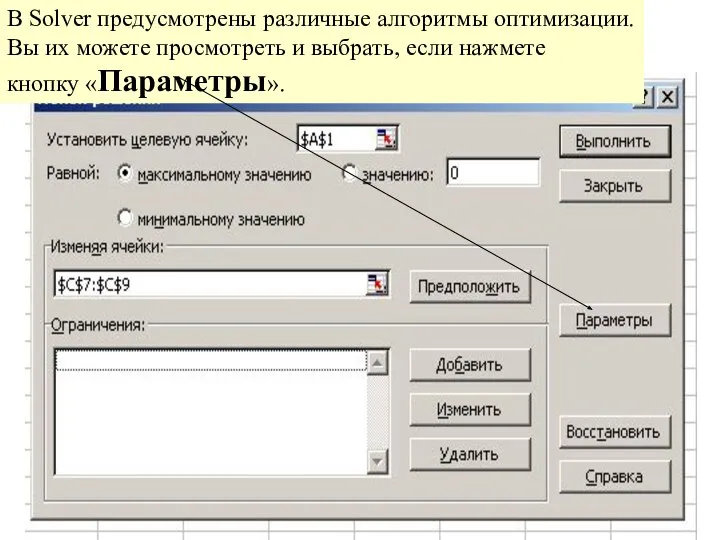
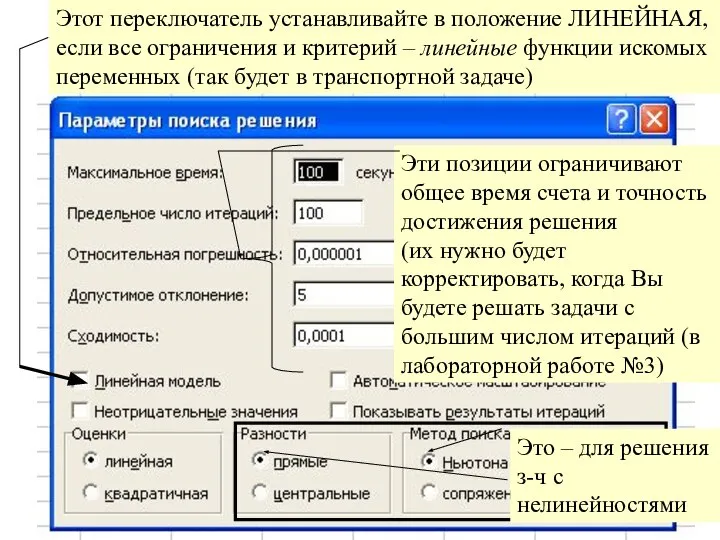
В Solver предусмотрены различные алгоритмы оптимизации.
Вы их можете просмотреть и выбрать, если нажмете
кнопку «Параметры».

Окошко «Параметры»
Этот переключатель устанавливайте в положение ЛИНЕЙНАЯ,
если все ограничения и критерий – линейные функции искомых
переменных (так будет в транспортной задаче)
Эти позиции ограничивают общее время счета и точность достижения решения
(их нужно будет корректировать, когда Вы будете решать задачи с большим числом итераций (в лабораторной работе №3)
Это – для решения
з-ч с нелинейностями

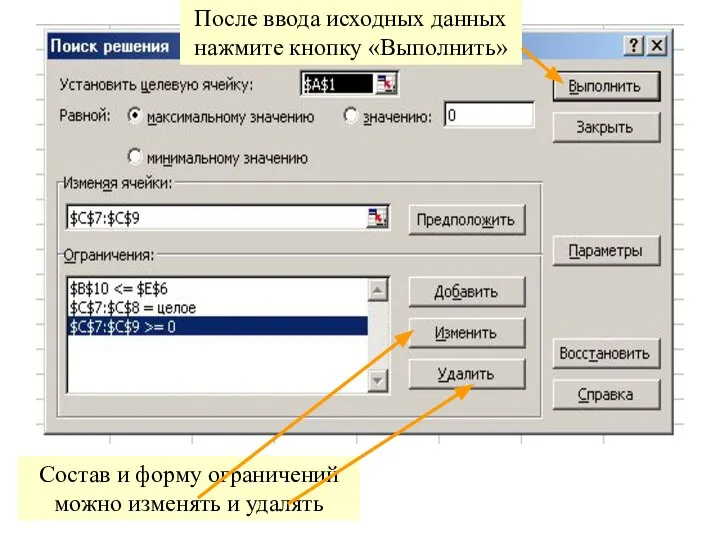
Состав и форму ограничений можно изменять и удалять
После ввода исходных данных нажмите кнопку «Выполнить»

Если решение существует (т.е. Если система ограничений
непротиворечива), то Solver изменит значения указанных
Вами ячеек так, чтобы достичь экстремума критерия.
В противном случае появится сообщение:
Выполнение:

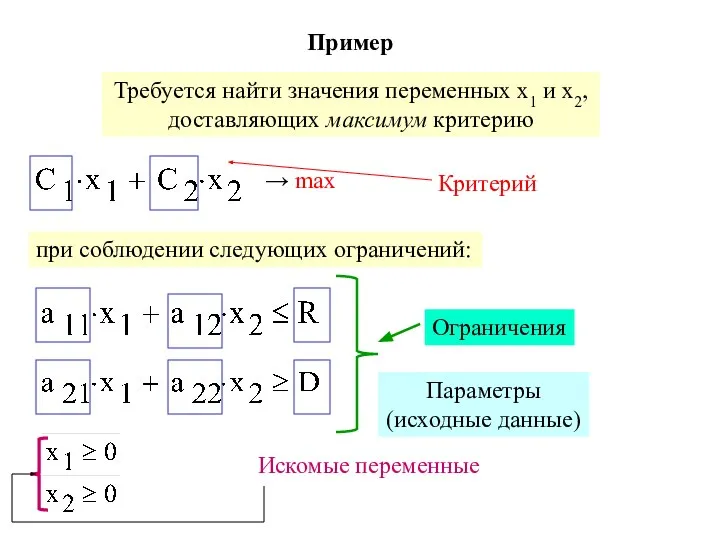
Пример
Требуется найти значения переменных х1 и х2,
доставляющих максимум критерию
→ max
при соблюдении следующих ограничений:
Искомые переменные
Критерий
Ограничения
Параметры
(исходные данные)

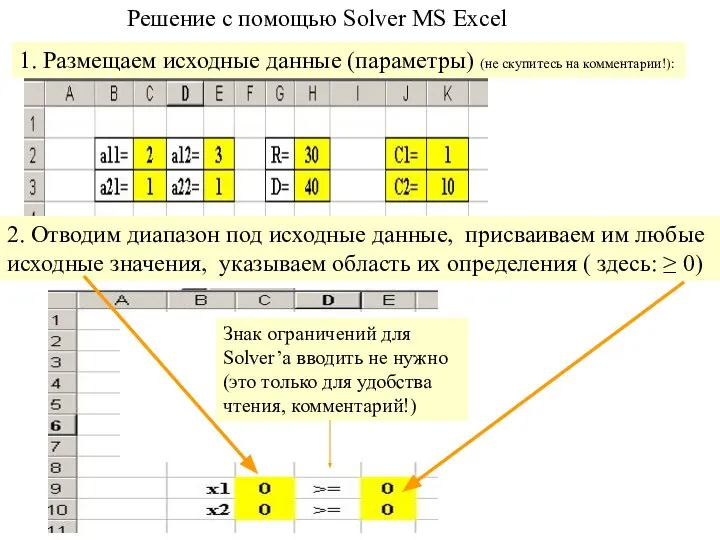
Решение с помощью Solver MS Excel
1. Размещаем исходные данные (параметры) (не скупитесь на комментарии!):
2. Отводим диапазон под исходные данные, присваиваем им любые исходные значения, указываем область их определения ( здесь: ≥ 0)
Знак ограничений для Solver’а вводить не нужно (это только для удобства чтения, комментарий!)

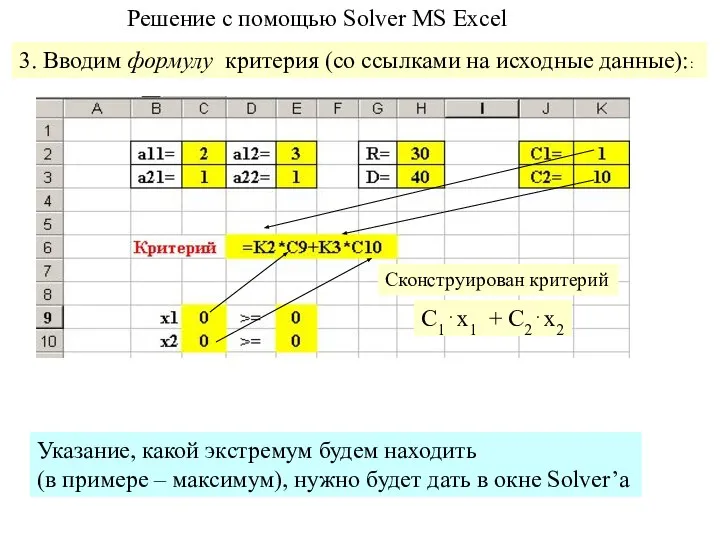
Решение с помощью Solver MS Excel
3. Вводим формулу критерия (со ссылками на исходные данные)::
С1⋅х1 + С2⋅х2
Сконструирован критерий
Указание, какой экстремум будем находить
(в примере – максимум), нужно будет дать в окне Solver’а

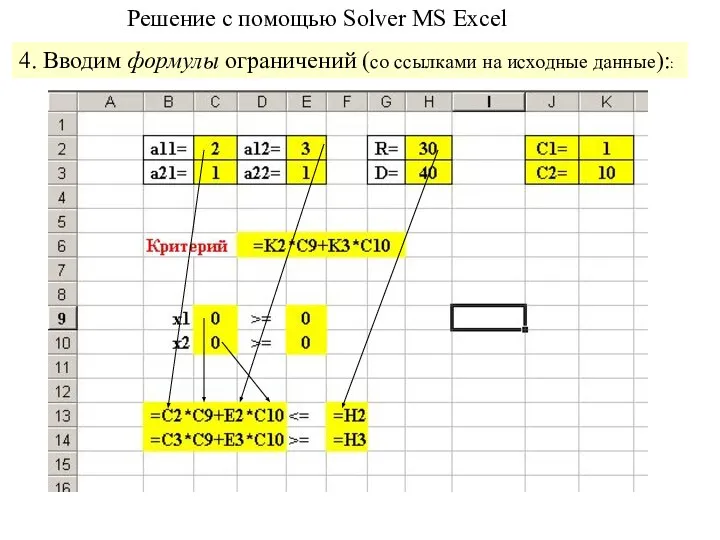
Решение с помощью Solver MS Excel
4. Вводим формулы ограничений (со ссылками на исходные данные)::

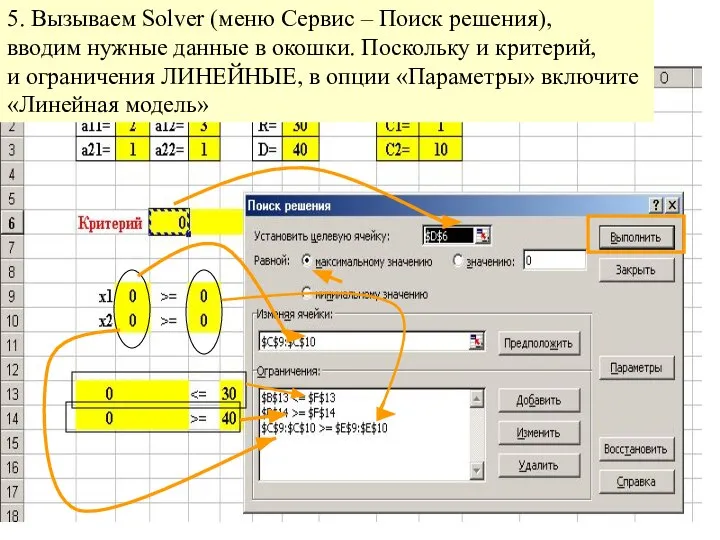
5. Вызываем Solver (меню Сервис – Поиск решения),
вводим нужные данные в окошки. Поскольку и критерий,
и ограничения ЛИНЕЙНЫЕ, в опции «Параметры» включите
«Линейная модель»

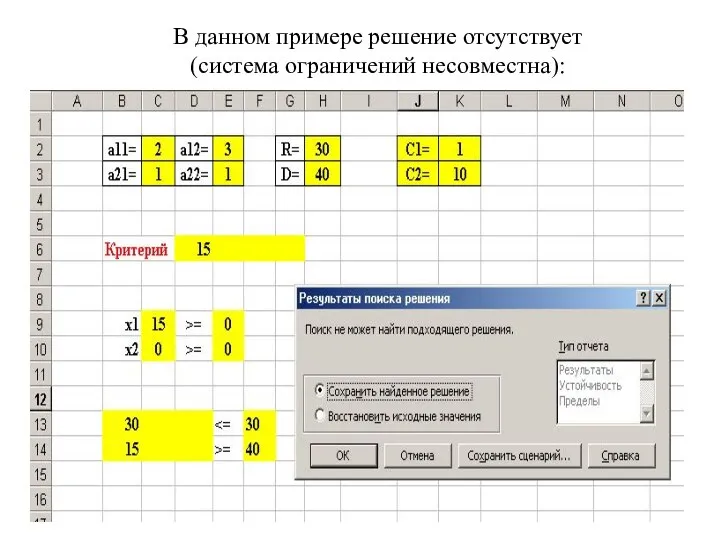
В данном примере решение отсутствует
(система ограничений несовместна):

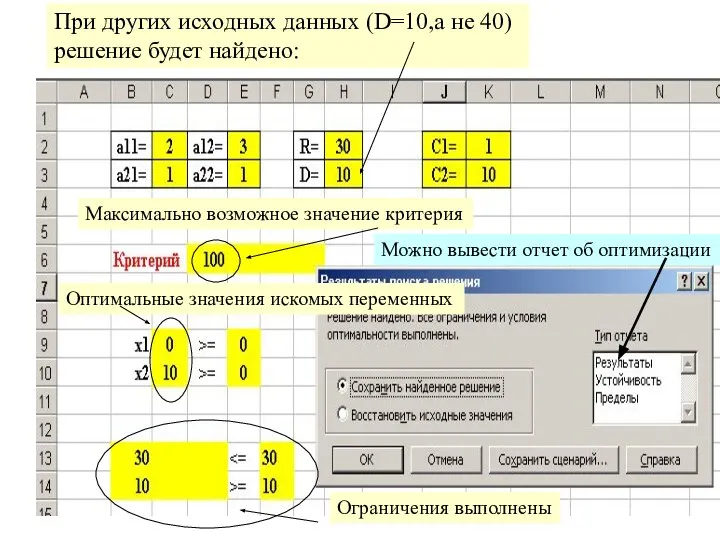
При других исходных данных (D=10,а не 40)
решение будет найдено:
Максимально возможное значение критерия
Оптимальные значения искомых переменных
Ограничения выполнены
Можно вывести отчет об оптимизации