Содержание
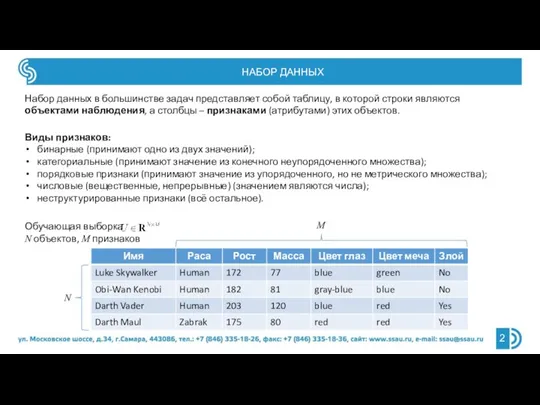
- 2. НАБОР ДАННЫХ Набор данных в большинстве задач представляет собой таблицу, в которой строки являются объектами наблюдения,
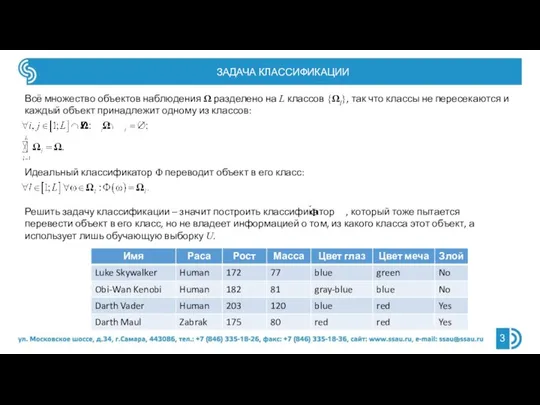
- 3. ЗАДАЧА КЛАССИФИКАЦИИ Всё множество объектов наблюдения Ω разделено на L классов {Ωl}, так что классы не
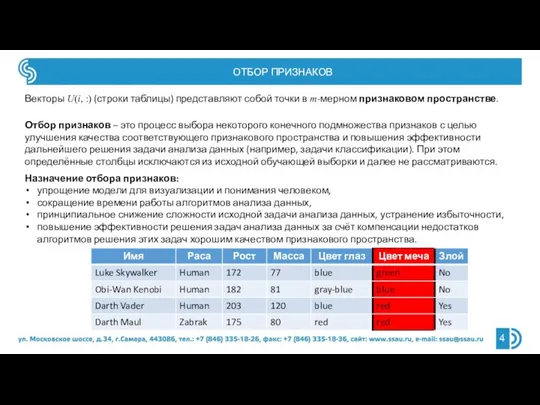
- 4. ОТБОР ПРИЗНАКОВ Векторы U(i, :) (строки таблицы) представляют собой точки в m-мерном признаковом пространстве. Отбор признаков
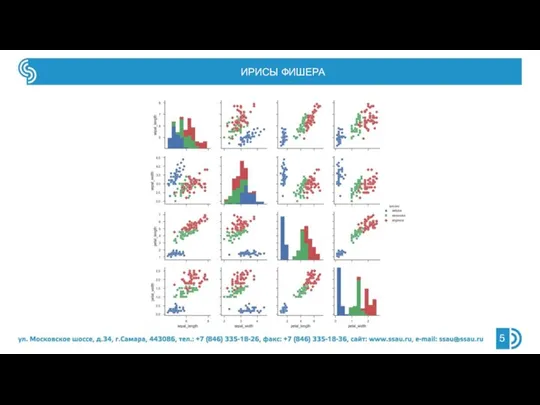
- 5. ИРИСЫ ФИШЕРА
- 6. ПОСТАНОВКА ЗАДАЧИ ОТБОРА ПРИЗНАКОВ Решить задачу отбора признаков – значит выбрать множество признаков так чтобы некоторый
- 7. КЛАССИФИКАЦИЯ АЛГОРИТМОВ ОТБОРА ПРИЗНАКОВ По характеру показателя качества признакового пространства J: Обёртки (wrappers) – методы отбора
- 8. ПОКАЗАТЕЛИ КАЧЕСТВА КЛАССИФИКАЦИИ Матрица ошибок (Confusion Matrix) Достоверность классификации (accuracy): – контрольная выборка Чувствительность (sensitivity, recall):
- 9. ПОКАЗАТЕЛИ КАЧЕСТВА ПРИЗНАКОВОГО ПРОСТРАНСТВА Матрица рассеяния внутри класса l: где – часть обучающей выборки из класса
- 10. ПОКАЗАТЕЛИ КАЧЕСТВА ПРИЗНАКОВОГО ПРОСТРАНСТВА Критерии дискриминантного анализа: Другие способы выбора внутриклассовой матрицы рассеяния: Другие способы выбора
- 11. ПОКАЗАТЕЛИ КАЧЕСТВА ПРИЗНАКОВОГО ПРОСТРАНСТВА Взаимная информация (mutual information): X – признаки случайного объекта, Y – класс
- 12. КЛАССИФИКАЦИЯ АЛГОРИТМОВ ОТБОРА ПРИЗНАКОВ По способу перебора подмножеств признаков: Жадные алгоритмы отбора признаков Упорядочение и отбор
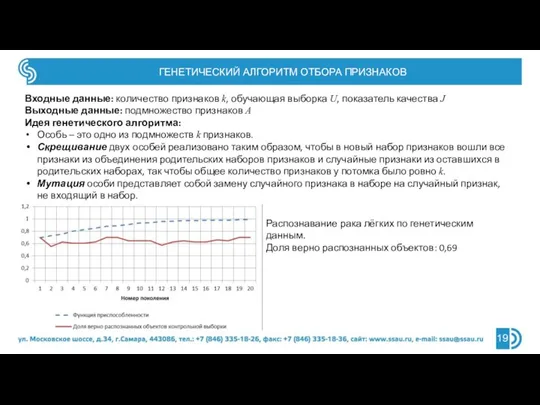
- 13. УПОРЯДОЧЕНИЕ И ОТБОР ПРИЗНАКОВ Входные данные: количество признаков k, обучающая выборка U, показатель качества J Выходные
- 14. ЖАДНЫЕ АЛГОРИТМЫ ОТБОРА ПРИЗНАКОВ Входные данные: количество признаков k, обучающая выборка U, показатель качества J Выходные
- 15. ЖАДНЫЕ АЛГОРИТМЫ ОТБОРА ПРИЗНАКОВ Модификации жадных алгоритмов могут быть основаны на их комбинировании. – шаг вперёд
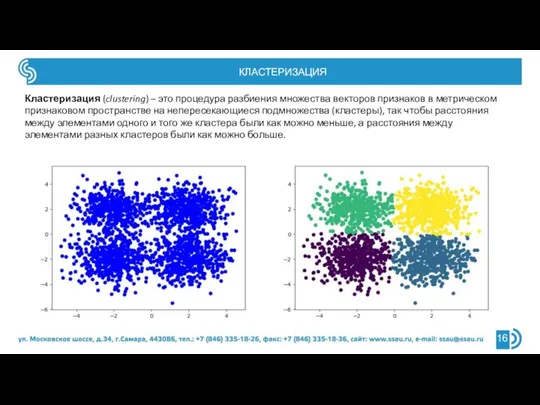
- 16. КЛАСТЕРИЗАЦИЯ Кластеризация (clustering) – это процедура разбиения множества векторов признаков в метрическом признаковом пространстве на непересекающиеся
- 17. КЛАСТЕРИЗАЦИЯ ПРИЗНАКОВ Входные данные: количество признаков k, обучающая выборка U, расстояние между признаками ρ Выходные данные:
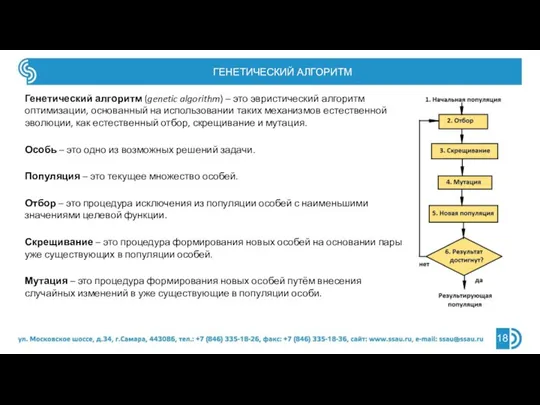
- 18. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ Генетический алгоритм (genetic algorithm) – это эвристический алгоритм оптимизации, основанный на использовании таких механизмов
- 19. ГЕНЕТИЧЕСКИЙ АЛГОРИТМ ОТБОРА ПРИЗНАКОВ Входные данные: количество признаков k, обучающая выборка U, показатель качества J Выходные
- 20. ОТБОР ПРИЗНАКОВ И ТЕОРИЯ ГРАФОВ Рассмотрим граф: вершины – подмножества признаков, рёбра – близкие между собой
- 21. СПИСОК ЛИТЕРАТУРЫ Guyon, I. An Introduction to Variable and Feature Selection / I. Guyon, A. Elisseeff
- 22. ЗАКЛЮЧЕНИЕ Когда подбор параметров классификатора уже не помогает повысить эффективность классификации, отбор признаков в некоторых случаях
- 24. Скачать презентацию














 PSR, MVC. Лекция 5
PSR, MVC. Лекция 5 Class Object
Class Object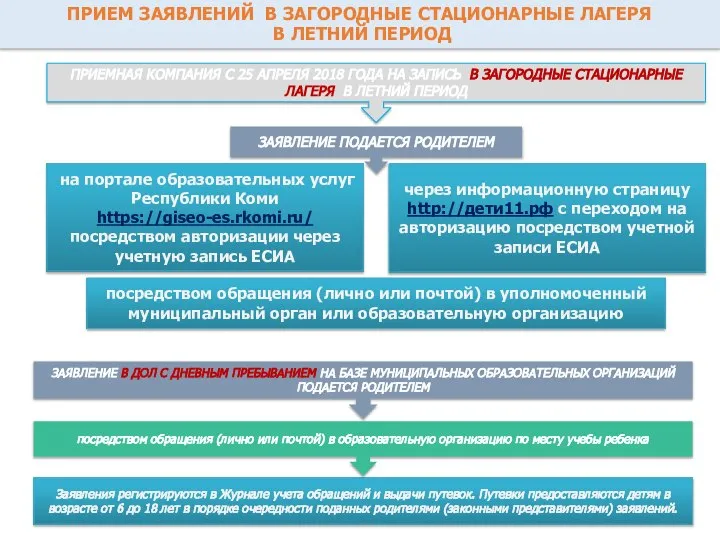 Прием заявлений в загородные стационарные лагеря в летний период
Прием заявлений в загородные стационарные лагеря в летний период Порождающие грамматики. (Лекция 2)
Порождающие грамматики. (Лекция 2) Знатоки интернет-безопасности
Знатоки интернет-безопасности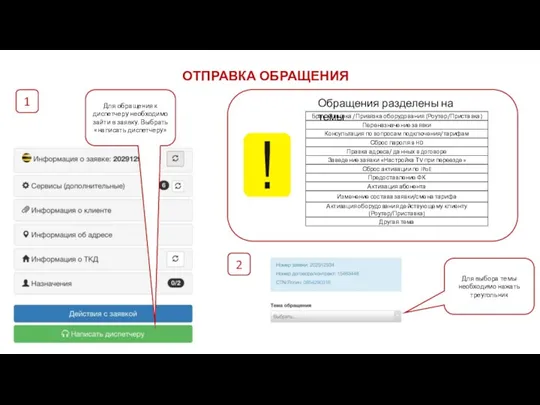 Отправка обращения
Отправка обращения Андройд UI-design мобильного интерфейса
Андройд UI-design мобильного интерфейса Введение в программирование на языке Python
Введение в программирование на языке Python Разработка веб-сайта для выбора автомобиля по заданным пользователем критериям
Разработка веб-сайта для выбора автомобиля по заданным пользователем критериям Введение в объектноориентированное программирование. Параметризованные типы
Введение в объектноориентированное программирование. Параметризованные типы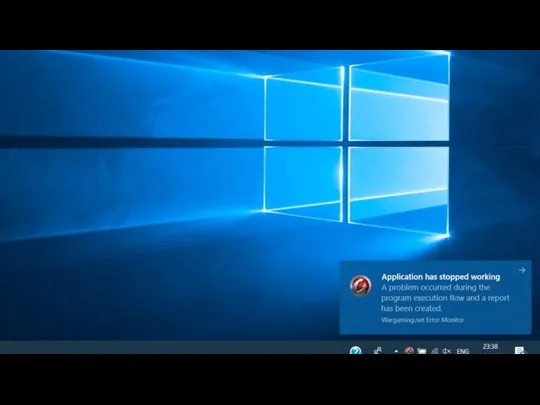 Скрин ошибки
Скрин ошибки Less iterations, more building
Less iterations, more building Организация подпрограмм. Программирование на яву. Лекция 5
Организация подпрограмм. Программирование на яву. Лекция 5 Основы программирования на языке Python. Написание программы в Python
Основы программирования на языке Python. Написание программы в Python Прикладное программирование на PHP
Прикладное программирование на PHP Файл и файловая система
Файл и файловая система Библиотека на колёсах
Библиотека на колёсах Информационно-образовательная среда педагога
Информационно-образовательная среда педагога Процесс_первичной_приемки_палет_
Процесс_первичной_приемки_палет_ Организационное и информационное обеспечение фандрейзинга
Организационное и информационное обеспечение фандрейзинга Выделение блоков текста (тег <P>)
Выделение блоков текста (тег <P>) Выполнить работу в MS Office Word
Выполнить работу в MS Office Word Формирование интерфейса проекта
Формирование интерфейса проекта Системы счисления и ДЗ на 6_10
Системы счисления и ДЗ на 6_10 Методичка по созданию сайта
Методичка по созданию сайта Программно-аналитический комплекс управления энергетическими ресурсами
Программно-аналитический комплекс управления энергетическими ресурсами Приложение Food Secret
Приложение Food Secret