Содержание
- 2. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Последовательность х – n-мерный двоичный
- 3. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 1 способ – последовательное рассмотрение
- 4. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Определения Обозначение О(…) является оценкой
- 5. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Определения Анализ сложности с точки
- 6. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 1 способ – метод перебора.
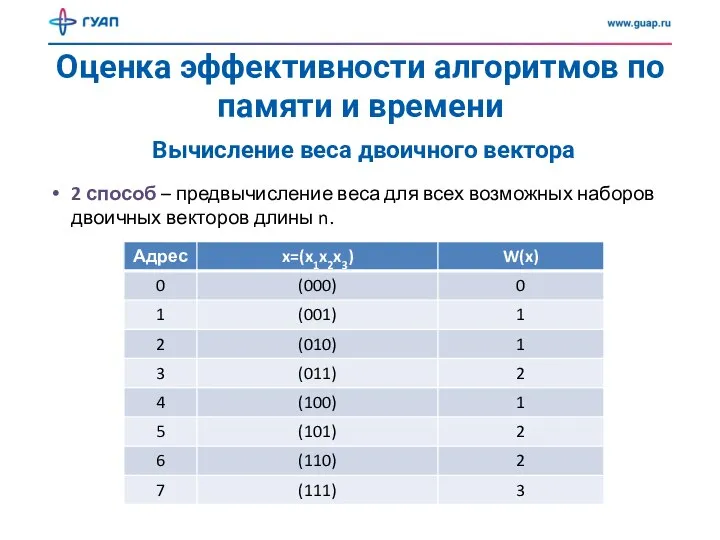
- 7. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 2 способ – предвычисление веса
- 8. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 2 способ – предвычисление веса
- 9. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 3 способ Операция , где
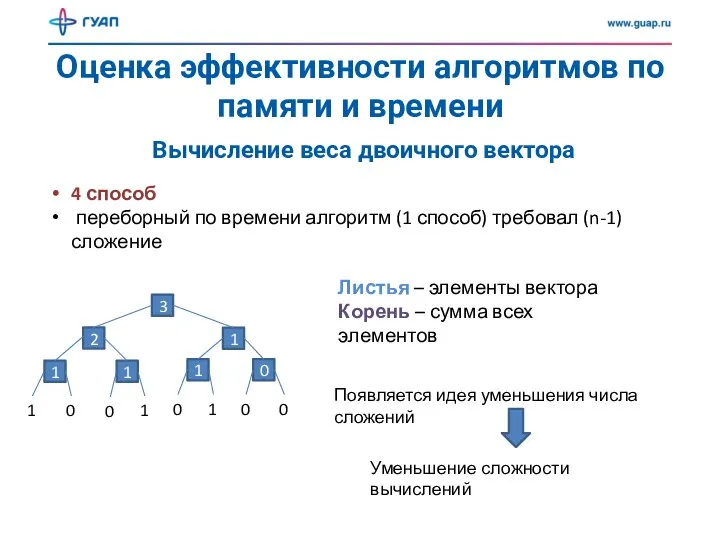
- 10. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 4 способ переборный по времени
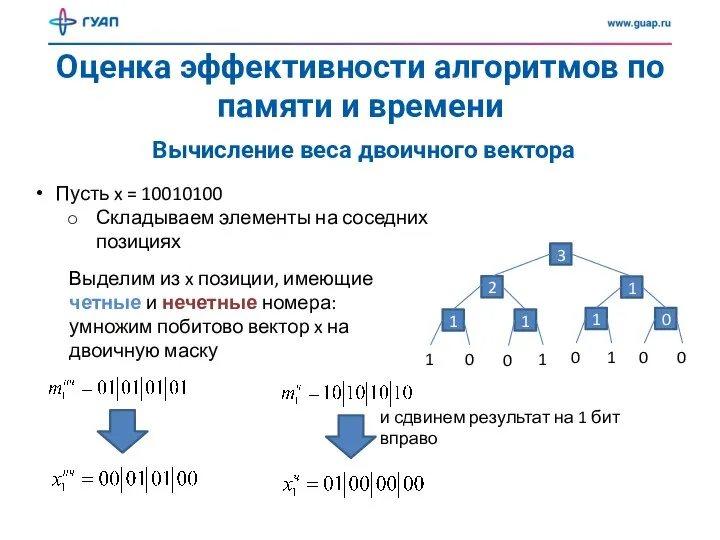
- 11. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Пусть x = 10010100 Складываем
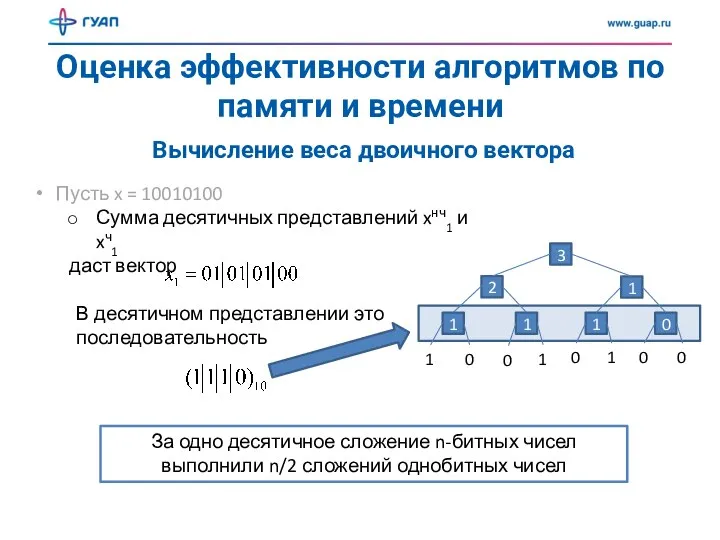
- 12. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Пусть x = 10010100 Сумма
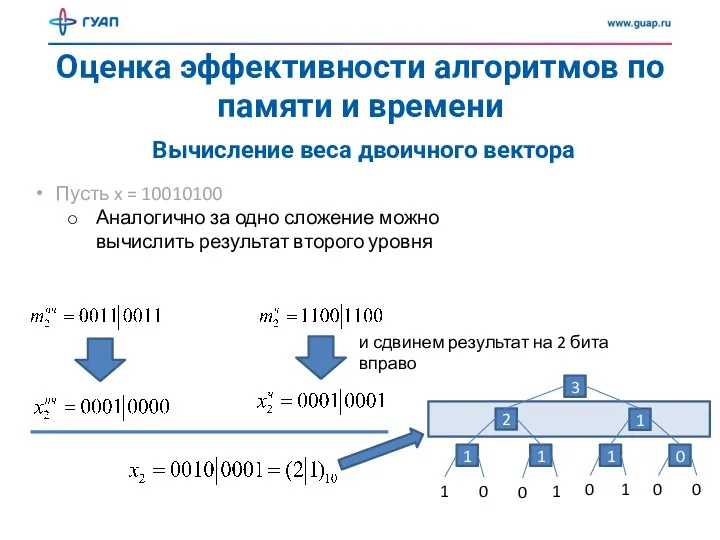
- 13. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Пусть x = 10010100 Аналогично
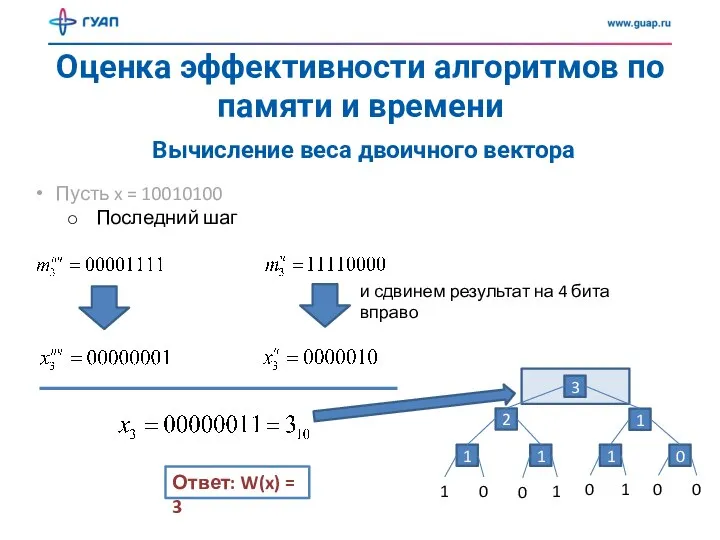
- 14. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора Пусть x = 10010100 Последний
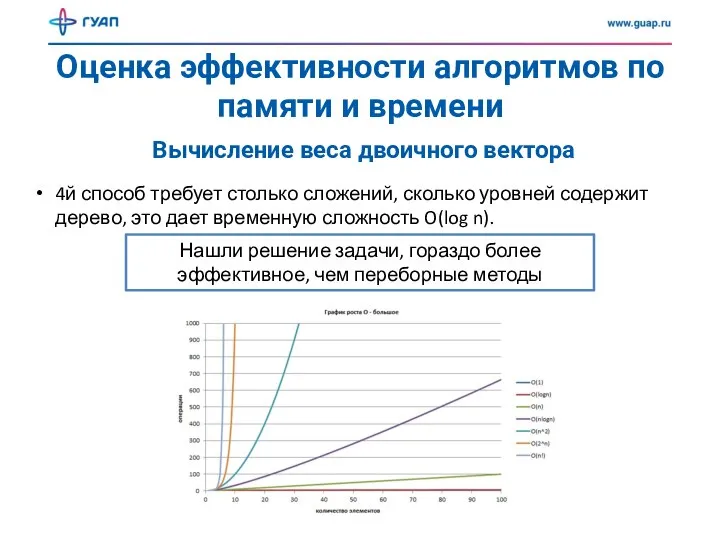
- 15. Оценка эффективности алгоритмов по памяти и времени Вычисление веса двоичного вектора 4й способ требует столько сложений,
- 17. Скачать презентацию







 Библиотека Кировских островов
Библиотека Кировских островов Итераторы и функциональные объекты
Итераторы и функциональные объекты Основы программирования (на языке Си). Массивы
Основы программирования (на языке Си). Массивы Проект Витрина
Проект Витрина Шаблоны писем
Шаблоны писем Профессия гейм-дизайнер
Профессия гейм-дизайнер Урок - игра Основы информатики
Урок - игра Основы информатики Мировой класс лидирующих компаний в цифровой струйной печати
Мировой класс лидирующих компаний в цифровой струйной печати Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера
Архитектура современной ЭВМ. Состав и характеристики комплектующих современного персонального компьютера Skype-конференция
Skype-конференция 3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами
3. Выбор жизненного цикла ИТ-проекта.Использование гибких подходов в управлении ИТ-проектами Примеры использования внешних устройств. Программное обеспечение внешних устройств
Примеры использования внешних устройств. Программное обеспечение внешних устройств Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра
Создание комплексной системы обеспечения информационной безопасности инфраструктуры Росреестра Хранители Равновесия
Хранители Равновесия База данных
База данных Технические новинки первой мировой войны
Технические новинки первой мировой войны Структуры данных: стеки, деки, очереди
Структуры данных: стеки, деки, очереди Интерактивная доска (ИД)
Интерактивная доска (ИД) Презентация на тему Примеры моделирования
Презентация на тему Примеры моделирования  Информационные технологии. Тема № 3. Основы защиты информации
Информационные технологии. Тема № 3. Основы защиты информации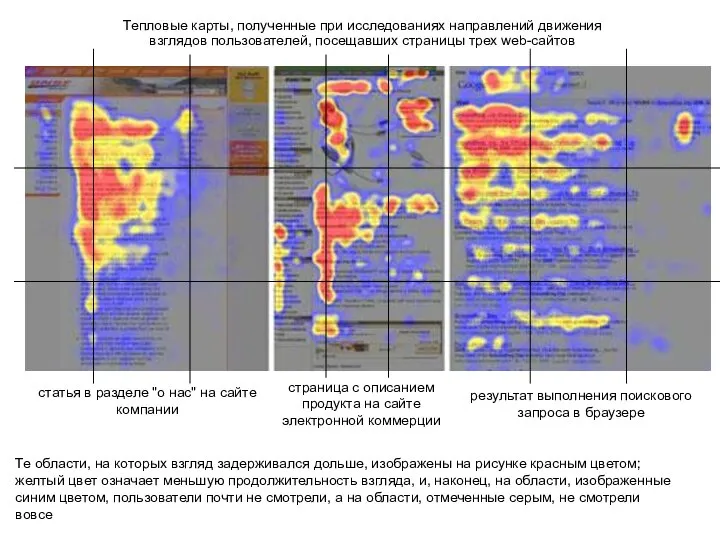 Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов
Тепловые карты, полученные при исследованиях направлений движения взглядов пользователей, посещавших страницы трех web-сайтов Функциональное программное обеспечение решения управленческих задач
Функциональное программное обеспечение решения управленческих задач Дизайн и графика. Web-страницы
Дизайн и графика. Web-страницы Источники пространственных данных. Их типы. Способы получения данных
Источники пространственных данных. Их типы. Способы получения данных Организация сетевого администрирования
Организация сетевого администрирования 3
3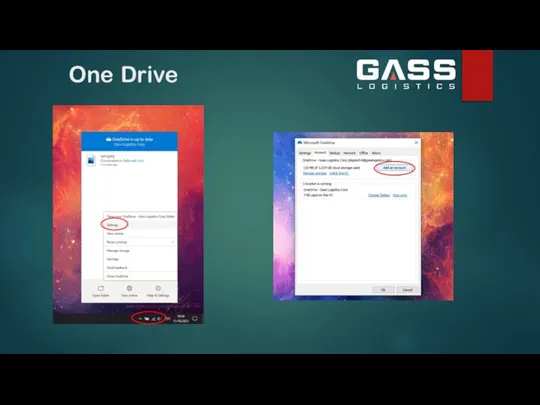 One Drive
One Drive Создание групп (сообществ) в образовательной сети
Создание групп (сообществ) в образовательной сети