Оценка эффективности информационной системы

1. Математические методы и модели принятия оптимальных управленческих решений
Типовые задачи оптимизации
Классификация задач оптимизации

1. Типовые задачи оптимизации
1. что, чем, где, когда, сколько заготавливать?
2. что, каких размеров, из какого материала делать?
1.1. Откуда появились вопросы
управленческое решение производства

1.1. Откуда появились вопросы
3. какой формы должен быть предмет, чтобы при заданной стоимости его объем был максимальным?
4. какой формы должен быть предмет заданного объема , чтобы его стоимость была минимальной?
управленческое решение проектирования

спроектировать изделие заданной стоимости с наилучшими свойствами
спроектировать изделие с заданными свойствами, но с наименьшей стоимостью
1.1. Откуда появились вопросы
две возможные постановки задачи проектирования

1.1. Откуда появились вопросы
5. кого, на какую работу назначить?
6. когда та или иная взаимосвязанные работы должны быть начаты и окончены для получения эффективного и оптимального решения?
управленческое решение распределения ресурсов
и оптимального распределения ресурсов во времени

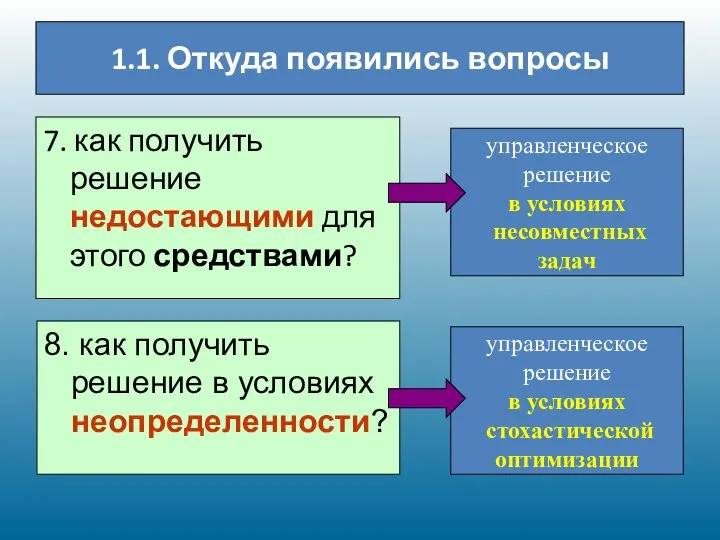
1.1. Откуда появились вопросы
7. как получить решение недостающими для этого средствами?
8. как получить решение в условиях неопределенности?
управленческое
решение
в условиях
несовместных
задач
управленческое
решение
в условиях
стохастической
оптимизации

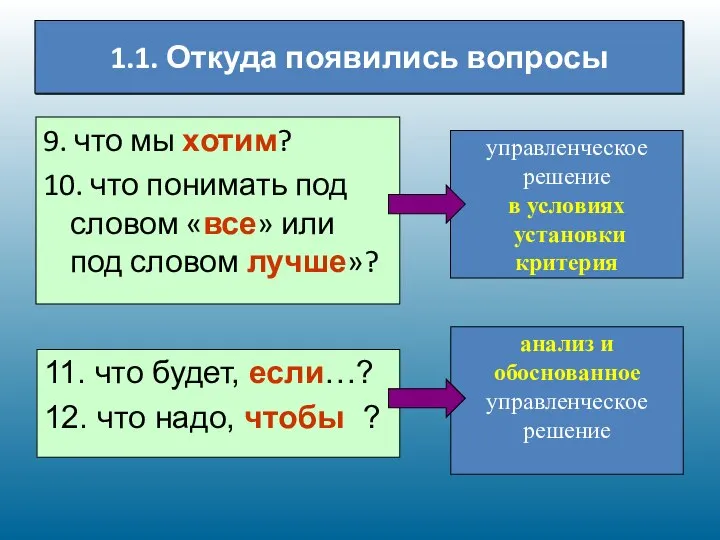
1.1. Откуда появились вопросы
9. что мы хотим?
10. что понимать под словом «все» или под словом лучше»?
11. что будет, если…?
12. что надо, чтобы ?
управленческое
решение
в условиях
установки критерия
анализ и
обоснованное
управленческое
решение
1.1. Откуда появились вопросы

1.1. Откуда появились вопросы - выводы
проектирование изделия: либо заданной стоимости с наилучшими свойствами, либо с заданными свойствами наименьшей стоимости;
задачи распределения ресурсов вообще и задачи распределения ресурсов во времени;
задачи стохастической оптимизации;
выбор критерия;
анализ принимаемого решения.

принятие оптимальных решений в управлении базируется на «трех китах»:
математической модели;
решении задачи на ЭВМ;
исходных данных.
1. Типовые задачи оптимизации
1.2. Основные методы решения задач

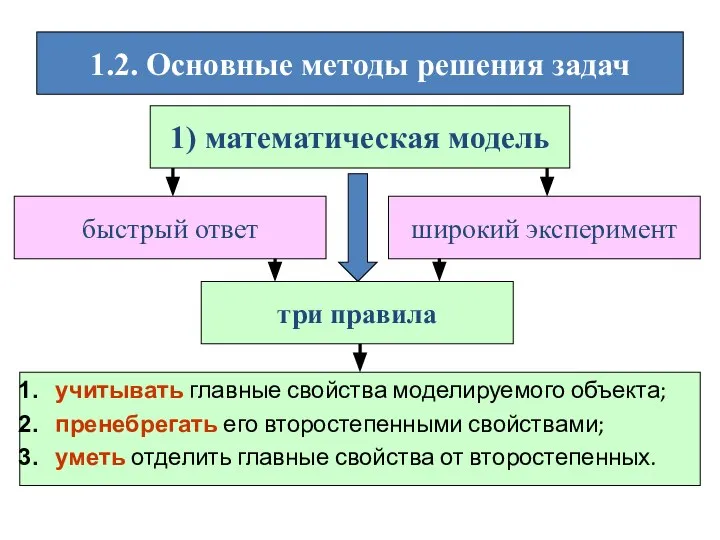
1.2. Основные методы решения задач
1) математическая модель
быстрый ответ
широкий эксперимент
три правила
учитывать главные свойства моделируемого объекта;
пренебрегать его второстепенными свойствами;
уметь отделить главные свойства от второстепенных.

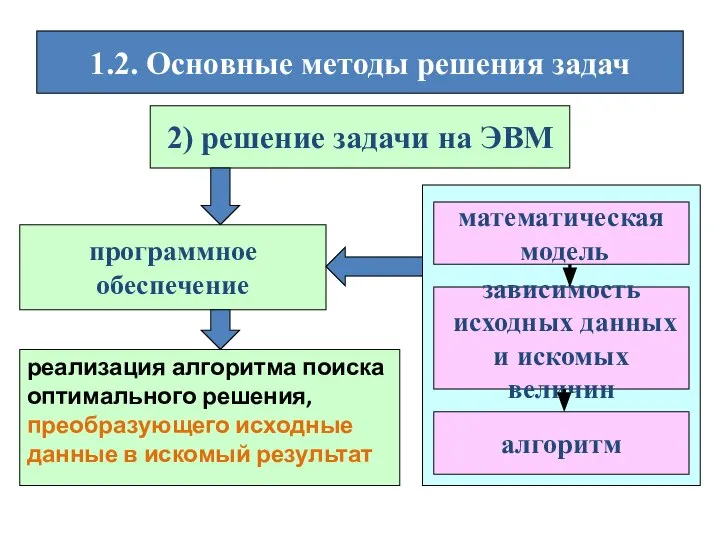
1.2. Основные методы решения задач
2) решение задачи на ЭВМ
математическая
модель
зависимость
исходных данных
и искомых величин
программное
обеспечение
реализация алгоритма поиска оптимального решения, преобразующего исходные данные в искомый результат
алгоритм

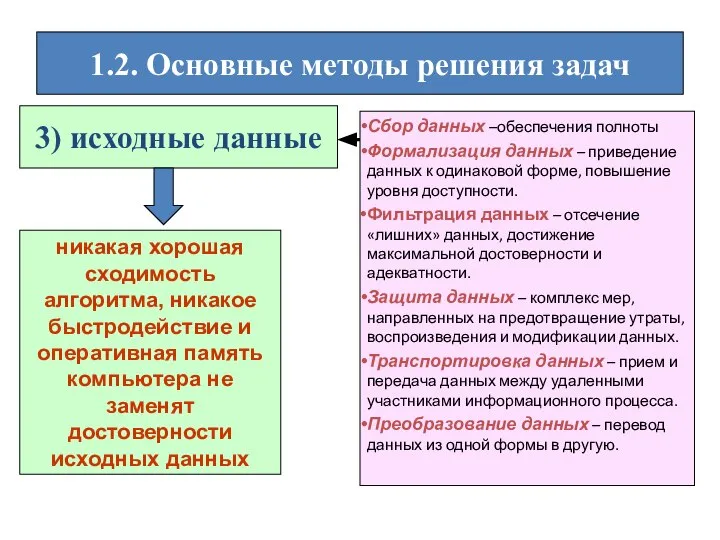
1.2. Основные методы решения задач
3) исходные данные
Сбор данных –обеспечения полноты
Формализация данных – приведение данных к одинаковой форме, повышение уровня доступности.
Фильтрация данных – отсечение «лишних» данных, достижение максимальной достоверности и адекватности.
Защита данных – комплекс мер, направленных на предотвращение утраты, воспроизведения и модификации данных.
Транспортировка данных – прием и передача данных между удаленными участниками информационного процесса.
Преобразование данных – перевод данных из одной формы в другую.
никакая хорошая сходимость алгоритма, никакое быстродействие и оперативная память компьютера не заменят достоверности исходных данных

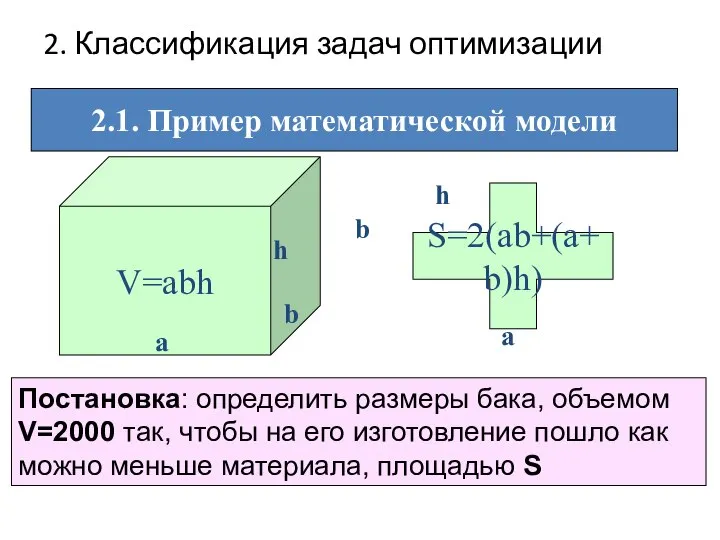
2. Классификация задач оптимизации
2.1. Пример математической модели
V=abh
S=2(ab+(a+b)h)
a
b
h
a
h
b
Постановка: определить размеры бака, объемом V=2000 так, чтобы на его изготовление пошло как можно меньше материала, площадью S

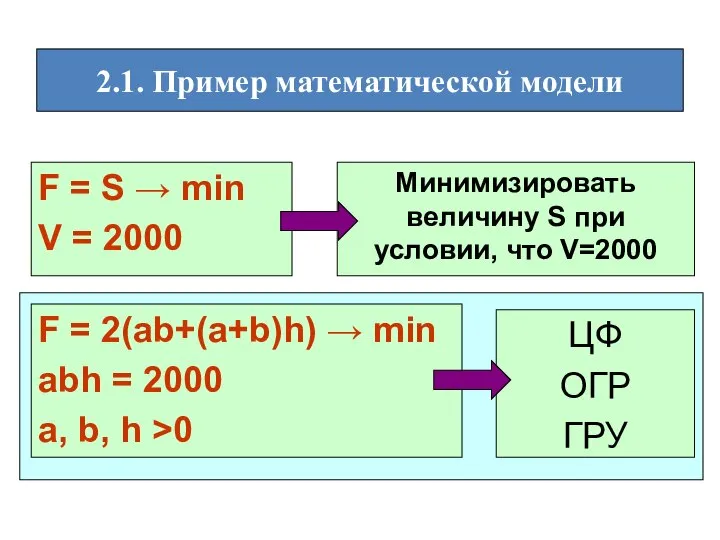
Минимизировать величину S при условии, что V=2000
2.1. Пример математической модели
F = S → min
V = 2000
ЦФ
ОГР
ГРУ
F = 2(ab+(a+b)h) → min
abh = 2000
a, b, h >0

2.2. Общий случай задачи оптимизации
Обозначим искомые переменные в общем виде x1=a, x2=b, x3=h
F = 2(x1x2+(x1+x2) x3) → min
x1x2x3 = 2000
x1, x2, x3 >0
F = f(x1x2x3) → min
g(x1x2x3) = b
x1, x2, x3 >0

2.2. Общий случай задачи оптимизации

2.2. Общий случай задачи оптимизации
1. ЦФ — целевая функция или критерий оптимизации, показывает, в каком смысле решение должно быть оптимальным, т. е. наилучшим.
2. ОГР — ограничения устанавливают зависимости между переменными.
3. ГРУ — граничные условия показывают, в каких пределах могут быть значения искомых переменных в оптимальном решении.

2.2. Общий случай задачи оптимизации-
выводы
задача имеет оптимальное решение, если она удовлетворяет двум требованиям:
1) Есть реальная возможность иметь более одного решения, т. е. существуют допустимые решения;
2) Имеется критерий, показывающий, в каком смысле принимаемое решение должно быть оптимальным, т. е. наилучшим из допустимых.

2. Критерии эффективности
Критерий качества ИС– субъективное мнение заказчика
Важно определить характеристики (свойства, функции), которые могут быть использованы при оценке качества ИС (критерии качества)
При оценке качества ИС желательно иметь методику, позволяющие получить интегральную оценку по установленному критерию.

2. Критерии эффективности
Формализация методики оценки
Задача: определить, какая из программных ИС) наиболее подходит для решения поставленной задачи (выступить в роли эксперта).
Пусть есть совокупный набор характеристик, характеризующих работу отдельных систем.
1. Открытость (модульный принцип)
2. Высокая степень интеграции с прикладным ПО (интеграция с ПО, ERP…)
3. Особенности хранения документов (распределенная БД…)
4. Маршрутизация документов (свободная, жесткая)
5. Разграничение доступа (полный контроль, право создавать, право редактировать…)
6. Отслеживание версий и подверсий документов
7. Аннотирование документов
8. Поддержка различных клиентских программ

3. Интегральная оценка Фишберна (методика)
Цель: получить сравнительную оценку нескольких систем по интегральному показателю, получаемому для каждой системы в отдельности.
1) Выбранные фактические характеристики назовем факторами и обозначим их через fj , где j = 1,2,…,m.
Через m обозначим количество факторов ( в нашем случае m=8).
2) Разобьем факторы по степени их важности для нас на группы Bi , i = 1, 2,…,n и укажем степень предпочтения этих групп так, что B1 > B2 > …> Bn

2. Интегральная оценка Фишберна (методика)
1) Определим группы факторов
Пусть, имеется 4 группы таких факторов (n=4):
B1– основные факторы;
B2– важные факторы;
B3– вспомогательные факторы;
B4– несущественные факторы.
2) Разобьем, например, факторы по группам так:
B1(f2, f4, f6) > B2(f1, f3) > B3(f5, f8) > B4(f7 )

2. Интегральная оценка Фишберна (методика)

2. Интегральная оценка Фишберна (методика)
Тогда, для каждой из групп важность факторов, входящих в эту группу, будет:

2. Интегральная оценка Фишберна (методика)
4) Получение интегральной оценки.
4.1) все факторы группируются по степени их учета в системе. Количество групп (Gq) и их категории учета также определяются экспертом (q=0,1,…,p).
Пусть такими группами для нашего случая будут (p=4):
G1– группа факторов, явно учитываемых в системе (необходимые факторы);
G2– группа факторов, учитываемых в системе не явно (не обязательно существуют, но влияют на характеристики системы);
G3– группа факторов, учитываемых для перспективы развития системы (не существуют, но определены и могут быть осуществимы)
G4– группа факторов, не учитываемая в системе (определены, существуют, но не влияют на характеристики системы).
Пусть:

2. Интегральная оценка Фишберна (методика)
4.2) по формуле
определяется количественная оценка Фишберна степени учета факторов (здесь q – номер группы).
В нашем случае

2. Интегральная оценка Фишберна (методика)
4.3) вычисляются нормированные оценки степени учета факторов по формуле:
В нашем случае

2. Интегральная оценка Фишберна (методика)
4.4) интегральная оценка получается по формуле: по формуле:
В нашем случае
= 1(0,145+0,145+0,145+0,11) + 0,7(0,09+0,11) +
+ 0,3(0,145) + 0(0,127) = 0,7285

2. Интегральная оценка Фишберна (методика)
Физический смысл данной интегральной оценки (0,7285)
отвечает задаче оценки качества ИС.
Если все факторы относятся только к первой группе B1 – «основные факторы», то F=1. Если все рассматриваемые факторы окажутся несущественными для выполнения целей, то F=0.
Различная степень субъективного (экспертного) распределения факторов по группам позволяет величине F изменяться в интервале [0,1] и, таким образом, оценивать качество данной ИС.
Получив интегральную оценку для одной ИС далее, по аналогичной схеме, оценивается следующая из предполагаемого набора. После получения интегральных оценок всех исследуемых экспертом систем эти интегральные оценки сравниваются, производится анализ качественной оценки и обосновывается выбор.
Таким образом, в результате сравнения получается экспертное заключение с обоснованием выбора ИС для ее эксплуатации.