оптимизации в данной постановке сводится к нахождению минимума функции трех переменных.
В Octave и Matlab для решение задачи поиска минимума функции нескольких переменных можно использовать функцию fmincon, которая находит минимум для скалярной функции нескольких переменных с ограничениями, начиная с начального приближения х0. В общем случае, эта задача относится к условной оптимизации.
Синтаксис: [x, val] = fmincon(fun,x0,A,b) начинает с начальной точки x0, находит значения х, при которых функция fun достигает минимума и возвращает минимальное значение целевой функции fun при условии выполнения ограничений в виде линейных неравенств A*x <= b. x0 может быть скаляром или вектором.








 Оптимальное планирование экскурсионных поездок школьников во время каникул
Оптимальное планирование экскурсионных поездок школьников во время каникул Автоматизация рабочего процесса письменного переводчика в XXI веке
Автоматизация рабочего процесса письменного переводчика в XXI веке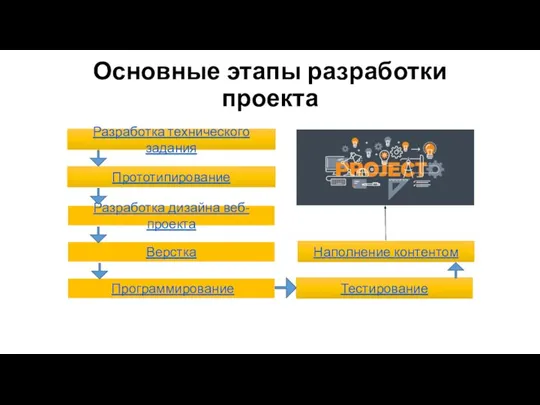 Основные этапы разработки проекта
Основные этапы разработки проекта История одной награды. Инструкция по поиску
История одной награды. Инструкция по поиску Создание сайта
Создание сайта Экономическая информатика
Экономическая информатика Способы подключения к Интернету
Способы подключения к Интернету Программное обеспечение компьютера
Программное обеспечение компьютера Функциональное программирование. Бестиповые арифметические выражения. (Лекция 2.2)
Функциональное программирование. Бестиповые арифметические выражения. (Лекция 2.2)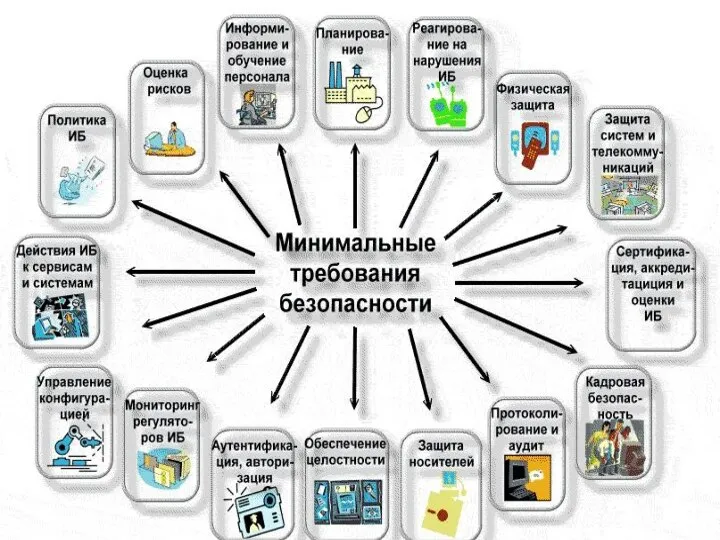 Минимальные требования безоапасности
Минимальные требования безоапасности Презентация на тему Язык программирования C++
Презентация на тему Язык программирования C++  Sequence to sequence. Модели и механизм внимания
Sequence to sequence. Модели и механизм внимания Безопасность в сети интернет
Безопасность в сети интернет Есептеуіш техниканың даму тарихы
Есептеуіш техниканың даму тарихы Компьютерная графика
Компьютерная графика Как можно представить информацию?
Как можно представить информацию? Печатать ПРЕЗЕНТАЦИЯ
Печатать ПРЕЗЕНТАЦИЯ Презентация на тему Урок Photoshop
Презентация на тему Урок Photoshop  Презентация без названия
Презентация без названия Добро пожаловать в мир AVON
Добро пожаловать в мир AVON Позиционирование. Параметры блока
Позиционирование. Параметры блока Структуры данных
Структуры данных Система управления базами данных моделирование и формализация
Система управления базами данных моделирование и формализация EchoBot. ChatBot. AppBot technology
EchoBot. ChatBot. AppBot technology Презентация на тему Основные положения Visual Basic
Презентация на тему Основные положения Visual Basic  Размещение и распределение рабочих мест Структурированной Кабельной Сети (СКС)
Размещение и распределение рабочих мест Структурированной Кабельной Сети (СКС) Исторический комментарий, как часть научно-справочного аппарата издания или исследования и самостоятельный жанр
Исторический комментарий, как часть научно-справочного аппарата издания или исследования и самостоятельный жанр 3605feab2893cfce779b9539ca2703f9
3605feab2893cfce779b9539ca2703f9