Содержание
- 2. Умови обчислення виразу піднесення до степеня
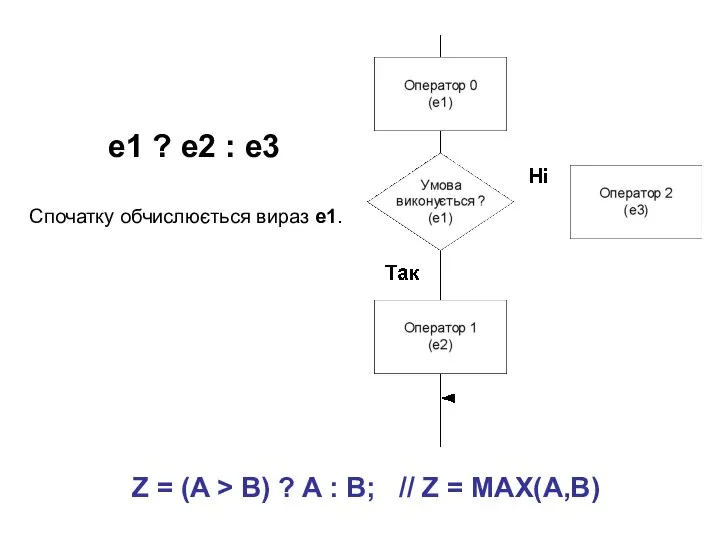
- 3. e1 ? e2 : e3 Спочатку обчислюється вираз е1. Z = (A > B) ? A
- 4. Завдання 2: Написати програму – календар, яка за введеною датою виводить день тижня прописом. Опис алгоритму
- 5. Завдання 3: Написати програму для розв’язання кубічного рівняння x3 + ax2 + bx + c =
- 6. та два комплексно – спряжених: , Якщо d > 0, то рівняння має один дійсний корінь:
- 7. YK=pow(Y,K) якщо K ∈ R, то Y >= 0 u=pow((-q/2+sqrt(d)),1/3.) ut=-q/2+sqrt(d) u = (ut>0) ? (
- 8. Якщо d = 0, то рівняння має три дійсних кореня:
- 9. Якщо d які, на жаль, можна обчислити лише наближено:
- 11. Скачать презентацию







 Системы управления базами данных (СУБД)
Системы управления базами данных (СУБД) Анализ информационной безопасности предприятия ОАО Альфа-банк
Анализ информационной безопасности предприятия ОАО Альфа-банк Информационные технологиии
Информационные технологиии Презентация "Поняття про програму. Запуск програми на виконання" - скачать презентации по Информатике
Презентация "Поняття про програму. Запуск програми на виконання" - скачать презентации по Информатике Применение баз данных в лечебных учреждениях
Применение баз данных в лечебных учреждениях Разработка координатного устройства для управления курсором и выдачи других команд ЭВМ
Разработка координатного устройства для управления курсором и выдачи других команд ЭВМ А7 ЕГЭ по информатике
А7 ЕГЭ по информатике Объединение сайтов
Объединение сайтов Математические модеи
Математические модеи Avast Antivirus для операционных систем Windows, Mac OS, Android и iOS
Avast Antivirus для операционных систем Windows, Mac OS, Android и iOS Модули и библиотеки
Модули и библиотеки Структура теорем. Виды теорем, связанных с данной
Структура теорем. Виды теорем, связанных с данной Инструкция по использованию инфомата для записи к врачу в порядке электронной очереди с помощью портала пациента
Инструкция по использованию инфомата для записи к врачу в порядке электронной очереди с помощью портала пациента Интернет технологии
Интернет технологии Файл и файловая система
Файл и файловая система Дизайн проектирование (композиция, макетирование, современные концепции в искусстве)
Дизайн проектирование (композиция, макетирование, современные концепции в искусстве) Безопасность сетей - снифферы (sniffer)
Безопасность сетей - снифферы (sniffer)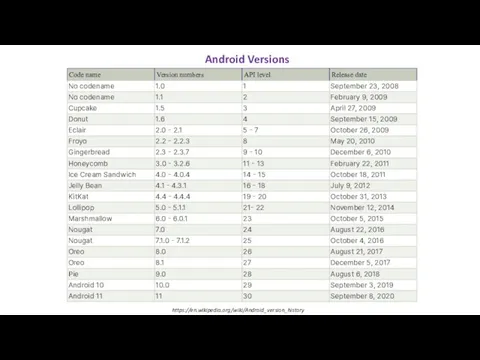 Android Versions
Android Versions Мобильное приложение для Android и iOS устройств
Мобильное приложение для Android и iOS устройств Информация. Виды и свойства
Информация. Виды и свойства Сравнительный анализ дизайна интернет-сайтов
Сравнительный анализ дизайна интернет-сайтов Программирование на языке C++
Программирование на языке C++ Платформа .Net
Платформа .Net MS Office Access
MS Office Access Алгоритмы. Вопросы
Алгоритмы. Вопросы Телекоммуникационная компания интернет-провайдер ООО Аванта Телеком
Телекоммуникационная компания интернет-провайдер ООО Аванта Телеком Разработка интернет магазина женской одежды при помощи CMS OpenCart
Разработка интернет магазина женской одежды при помощи CMS OpenCart Лазерный гравер на микроконтроллере Atmega 328
Лазерный гравер на микроконтроллере Atmega 328