Пирамидальная сортировка HeapSort. Пирамида Хеопса

Пирамидальная сортировка основана на алгоритме построения пирамиды.
Определение
Последовательность aL , aL+1 , … , aR называется пирамидой, если неравенство
ai ≤ min (a2i , a2i+1 )
выполняется для всех i, для которых хотя бы один из элементов a2i и a2i+1 существует.
Пирамидальная сортировка
или метод Вильямса – Флойда
( Williams, Floyd, 1964)

Пример
2 3 4 5 6 7 8 - пирамида
3 2 6 3 4 5 7
1 2 3 4 5 6 7 - не пирамида
1. Двустороннее усечение:
Если последовательность aL, aL+1 , ..., аR-1, aR –
пирамида, то aL+1 , ..., aR-1 тоже пирамида.
2. Если a1 , a2 , ..., an – пирамида,
то а1 – минимальный элемент пирамиды.
3. Если a1 , ..., an – произвольная
последовательность, то an/2 , .., an – пирамида.
Свойства пирамиды

Построение пирамиды
Пусть aL+1 , …, aR - пирамида,
необходимо добавить элемент Х,
чтобы получить новую пирамиду aL , …, aR.
Новый элемент добавляем в начало, расширяя последовательность влево.
Если aL удовлетворяет условию пирамиды, то пирамида построена.

Построение пирамиды
Иначе найдутся такие a2L или a2L+1 , что не будут удовлетворять условию пирамиды.
Возьмем минимальный элемент из a2L и a2L+1 , обозначим его за aj и обменяем с aL .
В результате получим a’L ≤ a2L и a’L ≤ a2L+1 , что удовлетворяет условию пирамиды.

Теперь элемент Х попал на место aj и для него необходимо проверить условие пирамиды, и так до конца массива.
Пример:
1 2 3 4 5 6 7 8
3 2 6 3 4 5 7
6 3 2 6 3 4 5 7
2 3 6 6 3 4 5 7
2 3 4 6 3 6 5 7
Пирамида
Пирамида
Построение пирамиды

Построение пирамиды (L ,R)
Алгоритм на псевдокоде
aL+1, …, a R – на входе пирамида (L+1,R)
aL – новый элемент
x := aL, i := L
DO
j := 2i
IF ( j>R) OD FI
IF ( j
IF ( x≤aj ) OD FI
ai= aj
i:=j
OD
ai:=x

Пирамидальная сортировка (HeapSort)
Первый этап. Построение пирамиды из элементов массива.
В соответствии со свойством 3 правая часть массива уже пирамида. Будем добавлять по одному элементу слева, расширяя пирамиду, пока в нее не войдут все элементы массива.
Второй этап. Собственно сортировка.
По свойству 2 в пирамиде первый элемент минимальный. Производим двустороннее усечение пирамиды: уберем элементы а1 и аn. По свойству 1 a2, .., an-1 – пирамида. Поставим элемент а1 на последнее место, а элемент аn добавим к пирамиде a2,..,an-1. Отсекаем последний элемент и повторяем действия, пока пирамида не исчезнет.

| L := ⎣n/2⎦
| DO ( L>0 )
1 | Построение пирамиды (L, n)
| L := L-1
| OD
| R := n
| DO ( R>1)
2 | a1↔aR
| R := R-1
| Построение пирамиды (1, R)
| OD
Пирамидальная сортировка (HeapSort)
Алгоритм на псевдокоде

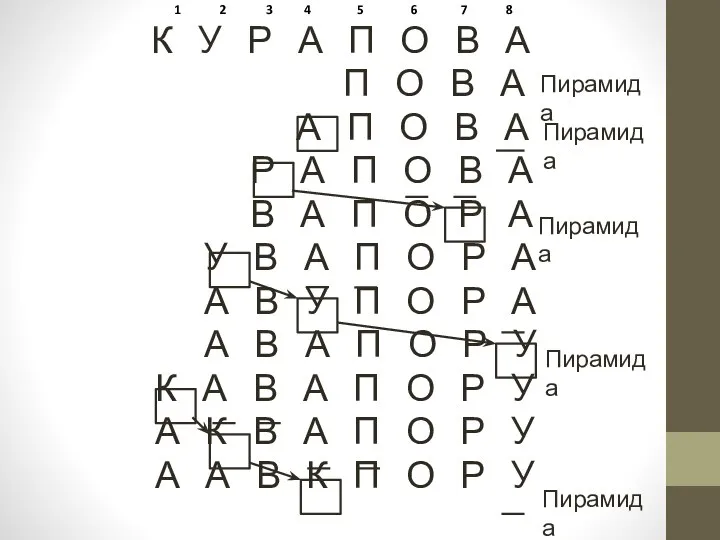
1 2 3 4 5 6 7 8
К У Р А П О В А
П О В А
А П О В А
Р А П О В А
В А П О Р А
У В А П О Р А
А В У П О Р А
А В А П О Р У
К А В А П О Р У
А К В А П О Р У
А А В К П О Р У
Пирамида
Пирамида
Пирамида
Пирамида
Пирамида

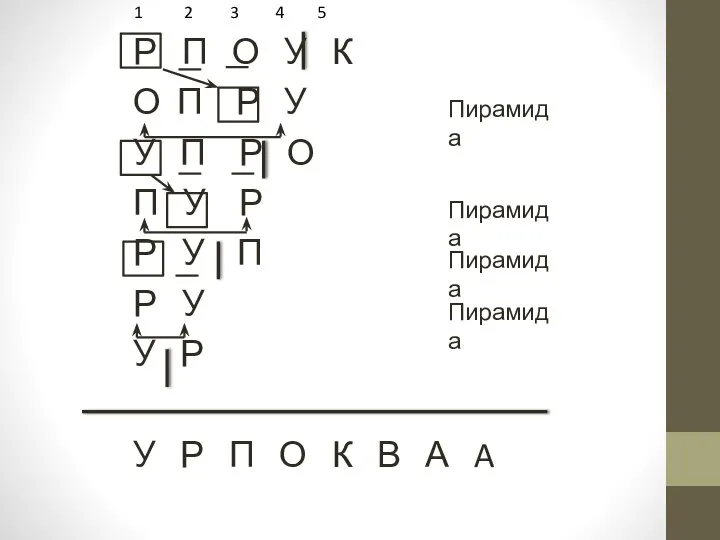
1 2 3 4 5 6 7 8
А А В К П О Р У
У А В К П О Р А
А У В К П О Р
А К В У П О Р
Р К В У П О А
В К Р У П О
В К О У П Р
Р К О У П В
К Р О У П
К П О У Р
Пирамида
Пирамида
Пирамида
Пирамида

Р П О У К
О П Р У
У П Р О
П У Р
Р У П
Р У
У Р
У Р П О К В А A
Пирамида
Пирамида
Пирамида
Пирамида
1 2 3 4 5