Содержание
- 2. Любая программа может состоять из основной программы и произвольного числа подпрограмм, включенных в основную программу. Подпрограмма
- 3. Обращение к подпрограмме В тексте основной программы вместо фрагмента, помещенного в подпрограмму, оформляется обращение к этой
- 4. Структура подпрограммы. Подпрограмма состоит из заголовка со списком параметров и тела подпрограммы, в котором реализуется алгоритм
- 5. Параметры подпрограммы Чтобы подпрограмма могла выполняться, ей надо получить данные из основной программы. Данные передаются через
- 6. Примеры использования подпрограмм-функций Задание 1. Вычислить периметр Р треугольника ΔABC, заданного на плоскости координатами его вершин:
- 7. Оформление подпрограммы-функции Блок-схема Псевдокод Турбо-Паскаль ДЛИНА(x1, y1, x2, y2) ДЛИНА:= d Конец функции Функция ДЛИНА (x1,
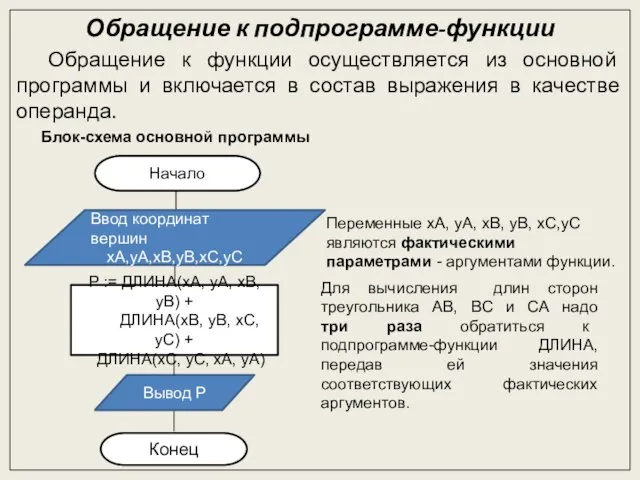
- 8. Обращение к подпрограмме-функции Обращение к функции осуществляется из основной программы и включается в состав выражения в
- 9. Программирование основной программы с использованием функции Псевдокод Начало программы Ввод координат вершин xA, yA, xB, yB,
- 10. Программирование основной программы с использованием функции Турбо-Паскаль Program PP_F; Var xA, yA, xB, yB, xC, yC,
- 12. Скачать презентацию








 Презентация на тему о вреде компьютера
Презентация на тему о вреде компьютера  Правила оформления библиографического списка
Правила оформления библиографического списка Архитектура аппаратных средств
Архитектура аппаратных средств Новая оплата пошлины 1400 на госуслугах
Новая оплата пошлины 1400 на госуслугах Программирование на языке С++
Программирование на языке С++ Програмные средства математических расчётов
Програмные средства математических расчётов PHP. Разработка блога
PHP. Разработка блога Как сформировать заявку на цикл
Как сформировать заявку на цикл Сети манипуляции: безопасность в условиях распространения деструктивного контента
Сети манипуляции: безопасность в условиях распространения деструктивного контента Комп'ютерна мережа
Комп'ютерна мережа Оценка эффективности информационной системы
Оценка эффективности информационной системы Введение в теорию трансляторов (практика 3)
Введение в теорию трансляторов (практика 3) Basta. Разработка стратегий, позволяющих сделать кампанию эффективной
Basta. Разработка стратегий, позволяющих сделать кампанию эффективной Формирование изображения на экране монитора. Обработка графической информации
Формирование изображения на экране монитора. Обработка графической информации Компьютерная графика
Компьютерная графика SIS: A system for Personal Information Retrieval and Re-Use
SIS: A system for Personal Information Retrieval and Re-Use Опасности глобальной информатизации гуманитарной науки
Опасности глобальной информатизации гуманитарной науки Программное обеспечение для кадровых служб компаний и рекрутинговых агентств
Программное обеспечение для кадровых служб компаний и рекрутинговых агентств Строки, дата и время в C#. Паттерны GoF. Лекция 4
Строки, дата и время в C#. Паттерны GoF. Лекция 4 Кампания Кем бы я был без интернета?
Кампания Кем бы я был без интернета? Автоматизация подписок и лайков. Массфолловинг
Автоматизация подписок и лайков. Массфолловинг Презентация на тему Язык гипертекстовой разметки - html
Презентация на тему Язык гипертекстовой разметки - html  Сети датацентров и виртуализация. Вычислительные сети и телекоммуникации
Сети датацентров и виртуализация. Вычислительные сети и телекоммуникации Методика SMART
Методика SMART Программное обеспечение. Лекция 3
Программное обеспечение. Лекция 3 Техника LOW POLY
Техника LOW POLY Реквием по фронту. Библиотека Korolev
Реквием по фронту. Библиотека Korolev Современные модели качества программных продуктов
Современные модели качества программных продуктов