Понятие о кодах

Основные характеристики:
Избыточность, определяется по формуле k=n-m,
где n- общее число знаков в коде; m- число информационных знаков. N чисел или слов в простом коде определяется:
m=log2N, k-число контрольных знаков. m=log24=2, k=1.
Относительная избыточность – R=k/m
Корректирующая способность определяется вероятностью обнаружения или исправления ошибок различных типов.
Вес W(A) кодовой комбинации А определяется количеством содержащихся в ней двоичных единиц.
Для А=111001, W(A)=Σai =4
Кодовое расстояние между двумя кодовыми комбинациями А и В определяется числом позиций, в которых их элементы не совпадают. Равно весу комбинации С, полученной поразрядным сложением А и В:
W(C)=W(A +B)= Σ(ai +bi)

Минимальная кодовое расстояние α
Простейший корректирующий код –с проверкой на четность, образуется добавлением одного избыточного разряда.
Мин кодовое расстояние с проверкой на четность α=2, обнаруживает одиночные ошибки и групповые нечетной кратности.
Код Хэмминга – для исправления одиночных ошибок (при α=3) или обнаружения без исправления двойных ошибок (α=4). N-значный код Хэмминга имеет m информационных разрядов и k контрольных. Число контрольных разрядов должно удовлетворять k>=log2(n+1), откуда m<=n-log2(n+1)
Пример шестизначный код Хэмминга n=6 k>=log27, k=3,
M = n – k = 3

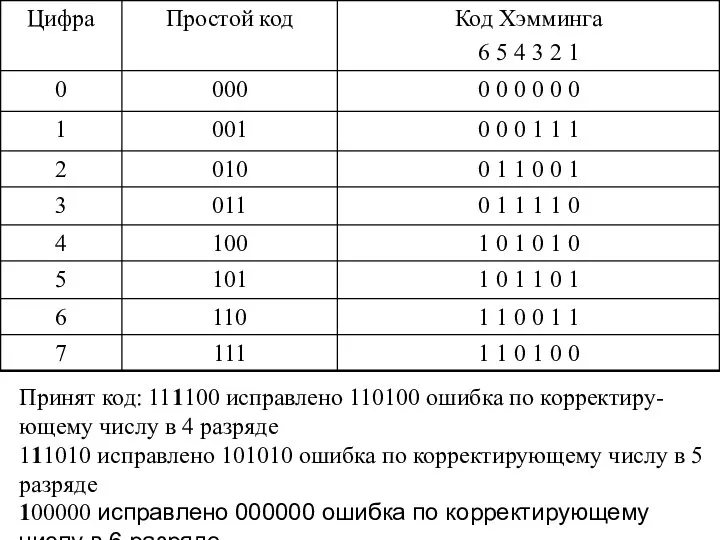
Принят код: 111100 исправлено 110100 ошибка по корректиру-ющему числу в 4 разряде
111010 исправлено 101010 ошибка по корректирующему числу в 5 разряде
100000 исправлено 000000 ошибка по корректирующему числу в 6 разряде

При проверке информации после приема возможны 3 случая
- отсутствие ошибок, к.ч.=0,
- одиночная ошибка, к.ч.=номер искаженного разряда
двойная ошибка, к.ч. не равно 0.
Циклический код – разновидность систематических кодов
Неприводимые многочлены (не могут быть представлены в виде произведения многочленов низших степеней, делится на себя или 1)при построении циклических кодов играют роль образующих полиномов.
Двоично-кодированное n - разрядное число представляется полиномом (n-1) степени некоторой переменной х, причем коэффициентами полинома являются двоичные знаки соответствующих разрядов. Запись, чтение и передача комбинаций производятся, начиная со старшего разряда (старший – справа).
Циклическая перестановка разрядов соответствует умноже-нию полинома на х, при котором xn заменяется 1 и перехо-дит в начало полинома.

Алфавитное кодирование
Пусть задано конечное множество A{a1,a2,…an}, называемое алфавитом. Элементы алфавита – буквы, последовательность букв – слово, n –длина слова. Множество слов в алфавите –А*. Если слово α= α1, α2, то α1 – это префикс слова, α2 – это постфикс (конец) слова. Алфавитное или побуквенное кодирование задается схемой или таблицей кодов δ:=< α1→ β1, α2→ β2, ,…, αn→, βn> , где αk ∈ A, βk∈Β*
Разделимое кодирование – такое, что любое слово, состоящее из элементарных кодов, единственным образом разлается на элементарные коды. (Двоично-десятичный код – разделимый).
Префиксное кодирование – такое, что элементарный код одной буквы не является префиксом элементарного кода другой буквы.
Для получения разделимой схемы алфавитного кодирования необходимо, чтобы длины элементарных кодов удовлетворяли определенному соотношению – неравенству Макмиллана.

Теорема.
Если числа l1, l2,…, ln соответствующие длинам элементарных кодов β1, β2, …, βn, удовлетворяют неравенству
∑2 –li <= 1,
то существует разделимая схема алфавитного кодирования δ→:= < α1→ β1, α2→β2, …, αn→βn

“Квадрат Полибия”
В Древней Греции (II в. до н. э.) был известен шифр, называемый “квадрат Полибия” (Полибий (200–120 гг. до н. э.) – древнегреческий историк.) . Это устройство представляло собой квадрат 5×5, столбцы и строки которого нумеровали цифрами от 1 до 5.
В каждую клетку записывалась одна буква (в греческом варианте одна клетка оказывалась пустой, а в латинском – в одну клетку помещали две буквы I, J). В результате каждой букве отвечала пара чисел по номеру строки и столбца
“Я мыслю, следовательно, существую”
Р. Декарт
Cogito ergo sum – лат.
34 22 24 44 34 15 42 22 34 43 45 32

Код Цезаря
В I в. н. э. Ю. Цезарь во время войны с галлами, переписываясь со своими друзьями в Риме, заменял в сообщении первую букву латинского алфавита А на четвертую D, вторую B – на пятую E, наконец последнюю – на третью:
ABCDEFGHIJKLMNOPQRSTUVWXYZ
DEFGHIJKLMNOPQRSTUVWXYZABC
YHQL YLGL YLFL
Veni vidi vici –
“Пришел, увидел, победил”
Ю. Цезарь. Донесение Сенату о победе
над понтийским царем

“Решетка Кардано”
Широко известны шифры, принадлежащие к классу “перестановка”, в частности, “решетка Кардано”2. Это прямоугольная карточка с отверстиями, чаще всего квадратная, которая при наложении на лист бумаги оставляет открытими лишь некоторые его части. Число строк и столбцов на карточке четное. Карточка сделана так, что при последовательном ее поворачивании каждая клетка лежащего под ней листа окажется занятой. Карточку поворачивают сначала вдоль вертикальной оси симметрии на 180°, а затем, вдоль горизонтальной оси, также на 180°. И вновь повторяют ту же процедуру.
2 Кардано Джероламо (1501–1576 гг.) – итальянский математик, философ и врач.

“Таблица Виженера”
Неудобство рассмотренных выше шифров очевидно, так как в случае использования стандартного алфавита таблица частот встречаемости букв алфавита позволяет определить один или несколько символов, а этого достаточно для вскрытия шифра, поэтому использовались различные приемы, для того чтобы затруднить дешифрование, например, использование “таблицы Виженера”, которая представляет собой квадратную таблицу с числом строк и столбцов, равным количеству букв алфавита. Чтобы получить шифрованный текст, находят очередной знак лозунга, начиная с первого, в вертикальном алфавите, а ему соответствующий знак сообщения в горизонтальном алфавите. На пересечении выделенных столбца и строки находим первую букву шифра. Очевидно, что ключом к такому шифру является используемый лозунг.
р а с к и н у л о с ь м о р е ш и р о к о
э о я к щ а п ы й ю й щ о в ч ф ш л ь ш ы

АБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯ
БВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯА
ВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБ
ГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБВ
ДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯФБВГ
ЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯФБВГД
ЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯФБВГДЕ
ЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖ
ИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗ
ЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИ
КЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙ
ЛМНОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙК
МНОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛ
НОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМ
ОПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМН
ПРСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНО
РСТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОП
СТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПР
ТУФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРС
УФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТ
ФХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУ
ХЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФ
ЦЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХ
ЧШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦ
ШЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧ
ЩЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШ
ЬЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩ
ЫЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬ
ЭЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧЩШЬЫ
ЮЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭ
ЯАБВГДЕЖЗИЙКЛМНОПРСТУФХЦЧШЩЬЫЭЮ

Виженер (1523–1596 гг.) – французский посол в Риме, написал большой труд о шифрах. Квадратный шифр Виженера на протяжении почти 400 лет не был дешифрован, считался недешифруемым шифром
“Одноразовый шифровальный блокнот”
Примером нераскрываемого шифра может служить так называемый “одноразовый шифровальный блокнот” – шифр, в основе которого лежит та же идея, что в шифре Цезаря. Назовем расширенным алфавитом совокупность букв алфавита, знаков препинания {. , : ; ! ? () – “ <пробел>}, число символов расширенного русского алфавита в данном варианте будет равно 44. Занумеруем символы расширенного алфавита числами от 0 до 43. Тогда любой передаваемый текст можно рассматривать как последовательность {an} чисел множества A={0,1,2,…,43}.
Предположим, что имеем случайную последовательность {cn} из чисел множества А той же длины, что и передаваемый текст – ключ.