Понятия информации и системы счисления

Информационные технологии Лекция 1
Понятие количества информации в статистической теории информации определяется на основе понятия вероятности, которое применяется для описания систем с неопределенностью.
Информация – это сведения или сообщения, которые снимают существовавшую до их получения неопределенность
Степень неопределенности измеряется величиной, которую в теории информации называют энтропией (Н).
Энтропия является функцией вероятности (р): Н=- lоg2 p
При р = 1 энтропия равна нулю, неопределенность полностью отсутствует.
В том случае, если в результате получения какого-то сообщения неопределенность полностью исчезает, количество информации (I) в этом сообщении равно энтропии I=H.

Информационные технологии Лекция 1
Количество информации, равное единице Н=1, принято называть битом.
Свое название бит (bit) единица измерения информации получила от английских слов binary digit (двоичная цифра).
Информация является положительной если неопределенность уменьшается и отрицательной если неопределенность увеличивается.
Рассмотрим в качестве примера сообщение “Do not lean of the window”, данное сообщение содержит 27 позиций и должна быть заполнена 27 символами (20 букв и 7 пробелов).
Следует отметить, что вероятность появления каждого символа на каждой позиции, не равна 1/27. Это связано с тем, что различные буквы латинского алфавита имеют различную частоту повторяемости в английском языке, а следовательно, и вероятность появления на каждой позиции. Для простоты примера будем считать вероятность появления каждого символа равной 1/27.

Информационные технологии Лекция 1

Информационные технологии Лекция 1
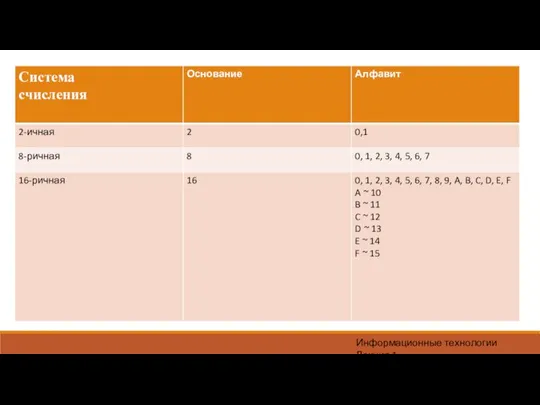
Системы счисления
Совокупность приемов наименования и изображения количественных величин с помощью ограниченного набора знаков будем называть системой счисления.
В настоящее время используются два вида систем счисления: позиционные и непозиционные системы счисления.
Наиболее известной непозиционной системой счисления является римская система счисления. В ней запись различных целых количеств производится с помощью цифр (1, 5, 10, 50, 100, 500 и 1000) I, V, X, L, C, D, M и т.д.
Запись MCMXСVII расшифровывается следующим образом: MCMXСVII = M + CM + XС + VII и означает число одна тысяча девятьсот девяносто семь.

Информационные технологии Лекция 1

Информационные технологии Лекция 1

Информационные технологии Лекция 1

Информационные технологии Лекция 1

Информационные технологии Лекция 1
Для перевода целого числа z из 10-ичной системы счисления в произвольную pичную применяется следующий алгоритм:
1) Определяется частное и остаток от деления числа z на p. Остаток будет очередной цифрой ai (i = 0, 1, 2, …) записи числа в новой системе счисления.
2) Если частное равно нулю, то перевод числа закончен, иначе к частному применяется пункт 1.
3) Цифры ai в записи числа нумеруются справа налево. Если p>10, то для цифр с числовыми значениями, большими или равными 10, вводятся специальные обозначения.

Информационные технологии Лекция 1
Перевод правильных дробей
Для перевода правильных дробей из одной системы счисления в другую, необходимо умножить исходную дробь и вновь полученные дробные части до получения числа заданной точности (Нулевой дробной части).
Пример:

Информационные технологии Лекция 1
Арифметические операции с системами счисления
Арифметические операции в различных системах счисления выполняются по тем же правилам, что и в десятичной системе счисления. Так, если при выполнении операции сложения двух целых чисел результат поразрядного сложения в каждом разряде меньше основания системы счисления, т.е.
x(i) + y(i) < p,
где i = -k, …, -1, 0,1,2,...n, а p - основание системы счисления, то в i-й разряд суммы z(i) записывается цифра, которая отображает количество, равное
z(i) = x(i) + y(i).
В том случае, если результат поразрядного сложения больше основания системы счисления или равен ему, т.е.
x(i) + y(i) ≥ p,
то в i-й разряд суммы записывается цифра, которая отображает количество, равное
z(i) = x(i) + y(i) − p.

Информационные технологии Лекция 1
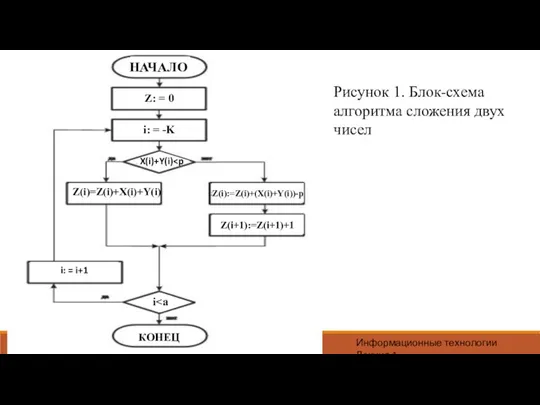
При этом в следующий разряд суммы z(i+1) переносится единица, которая должна учитываться при суммировании в (i+1)-м разряде. Это правило можно изобразить с помощью алгоритма поразрядного сложения двух чисел. Его блок-схема представлена на рисунке 1.
Операция вычитания является обратной к операции сложения. Поэтому при вычитании числа Y из числа X поступают по аналогичным правилам. То есть, если разряд вычитаемого меньше разряда уменьшаемого
x(i) > y(i),
то в i-й разряд частного записывается цифра, которая означает количество
r(i) = x(i)-y(i).
Если разряд вычитаемого будет больше разряда уменьшаемого, то в i-й разряд частного записывается цифра, обозначающая количество, равное
r(i) = x(i) + р - y(i),
а значение старшего разряда x(i+l) уменьшается на единицу.

Информационные технологии Лекция 1
Рисунок 1. Блок-схема алгоритма сложения двух чисел

Информационные технологии Лекция 1
Далее рассмотрим выполнение операций сложения и вычитания на примере шестнадцатеричной системы счисления.
Пусть X = 2FC(16), a Y = A3F(16).
Тогда сумма X + Y будет определяться следующим образом:
При поразрядном сложении С и F получается количество 27. Это количество не может быть записано с помощью цифр шестнадцатеричной системы счисления, т.е. возникает единица переноса в старший разряд. Следовательно, количество, которое будет записано в младшем разряде, равно 27 - 16 = 11, т.е. В. Во втором разряде результат поразрядного сложения цифр с учетом единицы переноса из младшего разряда имеет вид:
15 + 3 + 1 = 19

Информационные технологии Лекция 1
Этот результат также больше основания системы счисления. Поэтому во второй разряд суммы запишется величина 19 - 16 = 3, и появится единица переноса в третий разряд. С учетом этой единицы переноса в старшем разряде суммы должно быть отображено количество 10 + 2 + 1 = 13. Это количество меньше основания системы счисления и может быть записано цифрой D.
Операции умножения и деления рассмотрим на примере восьмеричной системы счисления. Для определения частных поразрядных произведений составим таблицу умножения (таблица 2). В этой таблице номера строк и столбцов соответствуют значениям сомножителей. Значения произведений по заданным значениям сомножителей находятся на пересечении соответствующих строк и столбцов.
Наиболее просто арифметические операции выполняются в двоичной системе счисления. Эта простота вызвана тем, что в двоичной системе счисления всего две цифры 0 и 1. Следовательно, максимальное количество, которое может быть записано в каждом разряде, равно одному. Количество, равное двум, записывается как 10.

Информационные технологии Лекция 1
Таблицы сложения, вычитания и умножения двоичных чисел весьма просты. Каждая из них состоит всего из четырех строчек (таблица 3, 4 и 5).
Таблица 2 Восьмеричная таблица умножения

Информационные технологии Лекция 1
Таблица 3 Двоичная таблица сложения
Таблица 4 Двоичная таблица вычитания
Таблица 5 Двоичная таблица умножения

Информационные технологии Лекция 1
С помощью этих таблиц операции сложения, вычитания, умножения и деления двоичных чисел выполняются так же, как и в десятичной системе счисления.
Пример :

Информационные технологии Лекция 1
Что касается умножения, то его можно выполнять как со сдвигом частичных произведений влево (умножение производить с младших разрядов множителей), так и со сдвигом вправо (получая частичные произведения при умножении начиная со старших разрядов множителей). Общее произведение в этом случае не изменится.

Информационные технологии Лекция 1
Способы представления чисел в памяти ЭВМ
При естественном представлении чисел для каждой двоичной цифры отводится один разряд в памяти вычислительной машины. Совокупность разрядов для записи числа носит название ячейки памяти.
Естественное представление числа требует, чтобы некоторое постоянное количество разрядов отводилось для хранения дробной части, а остальные – для хранения целой части числа. Для изображения знака числа в машине приняты следующие обозначения:
" + " = 0;
" − " = 1.
Схематичное изображение ячейки памяти при записи чисел с фиксированной точкой представлено на рисунке 2. В этой ячейке запятая (точка) фиксирована после четвертого разряда. Сама точка в ячейке не записывается.
Фиксированное положение точки при естественном представлении чисел определяет то, что такое представление числа носит название "С фиксированной точкой".

Информационные технологии Лекция 1
Рисунок 2. Схематичное изображение ячейки памяти при записи чисел с фиксированной точкой.
При выполнении арифметических операций с фиксированной точкой могут получаться результаты, целая часть которых содержит больше цифр, чем число разрядов ячейки, отведенных для хранения целой части.
При этом происходит переполнение разрядной сетки. Чтобы избежать этого, необходимо все величины, входящие в решаемую задачу, умножить заранее на множители, подобранные с таким расчетом, чтобы в процессе вычислений разрядная сетка не переполнялась. Эти множители носят название масштабных коэффициентов.

Информационные технологии Лекция 1
Подбор масштабных коэффициентов представляет собой нелегкую работу, для упрощения которой в большинстве ЭВМ запятая фиксируется непосредственно после знакового разряда (рисунок 3). При таком представлении в ячейке могут быть записаны только правильные дроби.
Представление чисел с фиксированной точкой в виде правильных дробей имеет ряд преимуществ при выполнении арифметических операций. Так, при сложении двух чисел переполнение может произойти только на один разряд, возникнет единица переноса в знаковый разряд. Чтобы зафиксировать результат переполнения, для записи знака числа надо отводить не один, а два разряда:
" + " = 00;
" − " = 11.
В этом случае при переполнении в знаковых разрядах результата будут записаны противоположные значения: "01" или "10". Переполнения разрядной сетки при выполнении операции умножения вообще никогда не произойдет, т.к. перемножение двух правильных дробей всегда в результате дает правильную дробь.

Информационные технологии Лекция 1
Рисунок 3. Схематичное изображение ячейки памяти при записи чисел с точкой, фиксированной после знакового разряда.
Однако выполнение операций с фиксированной точкой сопровождается необходимостью использования масштабных коэффициентов. Это можно избежать если каждая ячейка памяти машины, кроме знаковых и цифрового разрядов, будет иметь и некоторое количество разрядов, образующих указатель положения точки (рисунок 4).

Информационные технологии Лекция 1
Рисунок 4. Схематичное изображение ячейки памяти при записи чисел с плавающей точкой.

Информационные технологии Лекция 1
Чтобы понять, как изображаются числа в такой ячейке, рассмотрим произвольное число N. Это число всегда может быть представлено в виде:
N = m⋅ q p,
где q – основание системы счисления, |m| < 1, а p – целое.
Например, десятичное число 364,78 может быть представлено как
364,78 = 0,36478⋅ 10 3 = 0,036478⋅ 10 4 = 0,0036478⋅ 10 5
Двоичное число 1101,1001 может также быть представлено в виде:
1101,1001 = 0,11011001⋅ 10 100 = 0,011011001⋅ 10 101
(основание системы счисления и показатель степени записаны в двоичной системе счисления).
Такое представление чисел носит название записи "с плавающей точкой".