Слайд 3ЗАДАНИЕ №1
B некоторой стране автомобильный номер длиной 6 символов составляют из заглавных

букв (используются только 33 различных буквы) и десятичных цифр в любом порядке. Каждый такой номер в компьютерной программе записывается минимально возможным и одинаковым целым количеством байтов (при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов). Определите объём памяти, отводимый этой программой для записи 125 номеров. (Ответ дайте в байтах.)
Слайд 4РЕШЕНИЕ №1
Согласно условию, в номере могут быть использованы 10 цифр (0..9) и

33 буквы, всего 10 + 33 = 43 символов. Известно, что с помощью N бит можно закодировать 2N различных вариантов. Поскольку 25 < 43 < 26, то для записи каждого из 43 символов необходимо 6 бит.
Для хранения всех 6 символов номера нужно 6 * 6 = 36 бит, а т. к. для записи используется целое число байт, то берём ближайшее не меньшее значение, кратное восьми, это число 40 = 5 * 8 бит (5байт).
Тогда 125 номеров занимают 5 * 125 = 625 байт.
Слайд 5ЗАДАНИЕ №2
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из

11 символов и содержащий только символы А, Б, В, Г, Д, Е. Каждый такой пароль в компьютерной программе записывается минимально возможным и одинаковым целым количеством байт, при этом используют посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством бит. Определите, сколько байт необходимо для хранения 20 паролей.
Слайд 6РЕШЕНИЕ №2
Согласно условию, в пароле могут быть использованы 6 символов. Известно, что

с помощью N бит можно закодировать 2N различных вариантов. Поскольку 22 < 6 < 23, то для записи каждого из 6 символов необходимо 3 бита.
Для хранения всех 11 символов пароля нужно 3 · 11 = 33 бита, а т. к. для записи используется целое число байт, то берём ближайшее не меньшее значение, кратное восьми, это число 40 = 5 · 8 бит = 5 байт.
Тогда для записи двадцати паролей необходимо 5 · 20 = 100 байт.
Слайд 7САМОСТОЯТЕЛЬНОЕ ЗАДАНИЕ
При регистрации в компьютерной системе каждому пользователю выдаётся пароль, состоящий из

15 символов и содержащий только символы из 12-символьного набора: А, В, C, D, Е, F, G, H, К, L, M, N. В базе данных для хранения сведений о каждом пользователе отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего отведено 12 байт на одного пользователя.
Определите объём памяти (в байтах), необходимый для хранения сведений о 50 пользователях. В ответе запишите только целое число — количество байт.
Слайд 8РЕШЕНИЕ
На кодирование одного символа из 12-буквенного алфавита требуется 4 бита. Тогда на

один пароль необходимо бит. Минимальное количество байт, вмещающее 60 бит — 8. Итого на одного пользователя необходимо байт. А на 50 пользователей нужно байт.
Слайд 9ПОДСЧЕТ ПРОМЕЖУТОЧНОГО КОЛИЧЕСТВА ИНФОРМАЦИИ (№13)

Слайд 10ЗАДАНИЕ №1
Автоматическое устройство осуществило перекодировку информационного сообщения на русском языке, первоначально записанного

в 16-битном коде Unicode, в 8-битную кодировку КОИ-8. При этом информационное сообщение уменьшилось на 480 бит. Какова длина сообщения в символах?
Слайд 12ЗАДАНИЕ №2
В скачках участвуют 20 лошадей. Специальное устройство регистрирует прохождение каждой лошадью

финиша, записывая ее номер с использованием минимально возможного количества бит, одинакового для каждой лошади. Каков информационный объем сообщения, записанного устройством, если до финиша добрались только 15 из 20 участвовавших в скачках лошадей? (Ответ дайте в битах.)
Слайд 13РЕШЕНИЕ №2
Известно, что с помощью N бит можно закодировать 2N различных чисел. Поскольку

24 < 20 < 25, то для записи каждого из 20 номеров необходимо 5 бит памяти. Поскольку до финиша добрались только 15, то информационный объем сообщения составит 15⋅5 = 75 бит.
Слайд 16ЗАДАНИЕ №1
Производилась четырехканальная (квадро) звукозапись с частотой дискретизации 24 кГц и 16-битным

разрешением. В результате был получен файл размером 1800 Мбайт, сжатие данных не производилось. Определите приблизительно, сколько минут производилась запись.
В качестве ответа укажите ближайшее к времени записи целое число минут.
Слайд 18ЗАДАНИЕ №2
Производится двухканальная (стерео) звукозапись с частотой дискретизации 32 кГц и 32-битным

разрешением. Запись длится 3 минуты, её результаты записываются в файл, сжатие данных не производится. Определите приблизительно размер полученного файла (в Мбайт). В качестве ответа укажите ближайшее к размеру файла целое число, кратное пяти.
Слайд 20ЗАДАНИЕ №3
Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было

сохранить любое растровое изображение размером 128×128 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.
Слайд 21РЕШЕНИЕ №3
Один пиксель кодируется 8 битами памяти, так как 28 = 256.
Всего 128

* 128 = 27 · 27 = 214 пикселей.
Тогда объем памяти, занимаемый изображением 214 * 8 = 217 бит = 214 байт = 24 Кбайт = 16 Кбайт.
Слайд 22ЗАДАНИЕ №4
Автоматическая фотокамера производит растровые изображения размером 300 на 200 пикселей. При

этом объём файла с изображением не может превышать 30 Кбайт, упаковка данных не производится. Какое максимальное количество цветов можно использовать в палитре?
Слайд 23РЕШЕНИЕ №4
Объём растрового изображения находится как произведение количества пикселов в изображении на

объём памяти x, необходимый для хранения цвета одного пиксела: 300 · 200 · x < 30 · 213 бит, откуда x < 4,096 бит = 4 бит. Значит, в изображении можно использовать не более 24 = 16 цветов.
Ответ: 16.
Слайд 24ЗАДАНИЕ №5
Документ объёмом 80 Мбайт можно передать с одного компьютера на другой

двумя способами.
А. Сжать архиватором, передать архив по каналу связи, распаковать.
Б. Передать по каналу связи без использования архиватора.
Какой способ быстрее и на сколько, если
— скорость передачи данных по каналу связи составляет 225 бит в секунду;
— объём сжатого архиватором документа равен 35% исходного;
— время, требуемое на сжатие документа, – 15 секунд, на распаковку — 3 секунды?
Слайд 25РЕШЕНИЕ №5
Способ А. Общее время складывается из времени сжатия, распаковки и передачи.

Время передачи t рассчитывается по формуле t = Q / q, где Q — объём информации, q — cкорость передачи данных.
Найдём сжатый объём: 80 * 0,35 = 28 Мбайт
Переведём Q из Мбайт в биты: 28 Мбайт = 28 * 220 байт = 28 * 223 бит.
Найдём общее время: t = 15 с + 3 с + 28 * 223 бит / 225 бит/с = 18 + 7 с = 25 с.
Способ Б. Общее время совпадает с временем передачи: t = 80 * 223 бит / 225 бит/с = 20 с.
Видно, что способ Б быстрее на 25 − 20 = 5 с.
Ответ: Б5.
Слайд 26ЗАДАНИЕ №6
У Толи есть доступ к сети Интернет по высокоскоростному одностороннему радиоканалу,

обеспечивающему скорость получения информации бит в секунду. У Миши нет скоростного доступа в Интернет, но есть возможность получать информацию от Толи по низкоскоростному телефонному каналу со средней скоростью бит в секунду. Миша договорился с Толей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Мише по низкоскоростному каналу.
Компьютер Толи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах) с момента начала скачивания Толей данных до полного их получения Мишей?
Слайд 27РЕШЕНИЕ №6
Нужно определить, сколько времени будет передаваться файл объемом 5 Мбайт по

каналу со скоростью передачи данные 215 бит/с; к этому времени нужно добавить задержку файла у Толи (пока он не получит 512 Кбайт данных по каналу со скоростью 219 бит/с).
Переведём объём информации в Мб в биты: Q = 5 Мб = 5 * 220 байт = 5 * 223 бит.
Время задержки: = 512 кб / 219 бит/с = 2(9 + 10 + 3) - 19 c = 23 c.
Время скачивания данных Мишей: = 5*223 бит / 215 бит/с = 5*28 c.
Полное время: = 5 * 28 c + 23 c = (256 * 5 + 8) c = 1288 c.
Ответ: 1288.
Слайд 29ЗАДАНИЕ №1
Для 5 букв латинского алфавита заданы их двоичные коды (для некоторых

букв — из двух бит, для некоторых — из трех). Эти коды представлены в таблице:
Какой набор букв закодирован двоичной строкой 1100000100110?
Слайд 30РЕШЕНИЕ №1
Мы видим, что выполняется условие Фано: никакое кодовое слово не является

началом другого кодового слова, поэтому однозначно можем раскодировать сообщение с начала.
Разобьём код слева направо по данным таблицы и переведём его в буквы:
110 000 01 001 10 — b a c d e.
Слайд 31ЗАДАНИЕ №2
Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г

и Д, используется неравномерный двоичный код, позволяющий однозначно декодировать полученную двоичную последовательность. Вот этот код: А — 1; Б — 0100; В — 000; Г — 011; Д — 0101. Требуется сократить для одной из букв длину кодового слова так, чтобы код по-прежнему можно было декодировать однозначно. Коды остальных букв меняться не должны. Каким из указанных способов это можно сделать?
1) для буквы Г — 11
2) для буквы В — 00
3) для буквы Г — 01
4) это невозможно
Слайд 32РЕШЕНИЕ №2
Для однозначного декодирования получившееся в результате сокращения кодовое слово не должно

быть началом никакого другого. Первый вариант ответа не подходит, поскольку код буквы А является началом кода буквы Г. Второй вариант ответа подходит. Третий вариант ответа не подходит, т. к. в таком случае код буквы Г является началом кода буквы Д.
Правильный ответ указан под номером: 2.
Слайд 33ЗАДАНИЕ №3
Для кодирования некоторой последовательности, состоящей из букв И, К, Л, М,

Н, решили использовать неравномерный двоичный код, удовлетворяющий условию Фано. Для буквы Н использовали кодовое слово 0, для буквы К – кодовое слово 10. Какова наименьшая возможная суммарная длина всех пяти кодовых слов?
Примечание. Условие Фано означает, что никакое кодовое слово не является началом другого кодового слова. Это обеспечивает возможность однозначной расшифровки закодированных сообщений.
Слайд 34РЕШЕНИЕ №3
Нельзя использовать кодовые слова, которые начинаются с 0 или с 10.

11 также не можем использовать, поскольку тогда мы больше не сможем взять никакое другое кодовое слово, а нам их нужно пять. Поэтому берём трёхзначное 110. 111 опять же не можем использовать, потому что понадобиться ещё одно кодовое слово, а вместе с этим не останется больше свободных. Теперь осталось взять всего два слова и это будут 1110 и 1111. Итого имеем 0, 10, 110, 1110 и 1111 — 14 символов.
Слайд 35САМОСТОЯТЕЛЬНОЕ ЗАДАНИЕ
По каналу связи передаются сообщения, содержащие только четыре буквы: П, О,

С, Т; для передачи используется двоичный код, допускающий однозначное декодирование. Для букв Т, О, П используются такие кодовые слова: Т: 111, О: 0, П: 100.
Укажите кратчайшее кодовое слово для буквы С, при котором код будет допускать однозначное декодирование. Если таких кодов несколько, укажите код с наименьшим числовым значением.
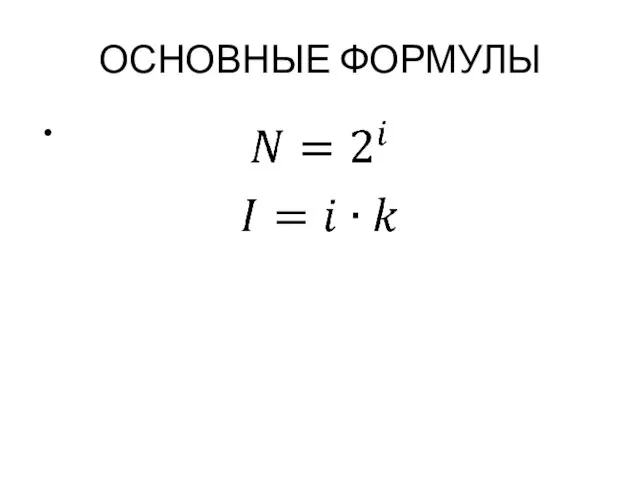

































 Презентация на тему о вреде компьютера
Презентация на тему о вреде компьютера  Правила оформления библиографического списка
Правила оформления библиографического списка Архитектура аппаратных средств
Архитектура аппаратных средств Новая оплата пошлины 1400 на госуслугах
Новая оплата пошлины 1400 на госуслугах Программирование на языке С++
Программирование на языке С++ Програмные средства математических расчётов
Програмные средства математических расчётов PHP. Разработка блога
PHP. Разработка блога Как сформировать заявку на цикл
Как сформировать заявку на цикл Сети манипуляции: безопасность в условиях распространения деструктивного контента
Сети манипуляции: безопасность в условиях распространения деструктивного контента Комп'ютерна мережа
Комп'ютерна мережа Оценка эффективности информационной системы
Оценка эффективности информационной системы Введение в теорию трансляторов (практика 3)
Введение в теорию трансляторов (практика 3) Basta. Разработка стратегий, позволяющих сделать кампанию эффективной
Basta. Разработка стратегий, позволяющих сделать кампанию эффективной Формирование изображения на экране монитора. Обработка графической информации
Формирование изображения на экране монитора. Обработка графической информации Компьютерная графика
Компьютерная графика SIS: A system for Personal Information Retrieval and Re-Use
SIS: A system for Personal Information Retrieval and Re-Use Опасности глобальной информатизации гуманитарной науки
Опасности глобальной информатизации гуманитарной науки Программное обеспечение для кадровых служб компаний и рекрутинговых агентств
Программное обеспечение для кадровых служб компаний и рекрутинговых агентств Строки, дата и время в C#. Паттерны GoF. Лекция 4
Строки, дата и время в C#. Паттерны GoF. Лекция 4 Кампания Кем бы я был без интернета?
Кампания Кем бы я был без интернета? Автоматизация подписок и лайков. Массфолловинг
Автоматизация подписок и лайков. Массфолловинг Презентация на тему Язык гипертекстовой разметки - html
Презентация на тему Язык гипертекстовой разметки - html  Сети датацентров и виртуализация. Вычислительные сети и телекоммуникации
Сети датацентров и виртуализация. Вычислительные сети и телекоммуникации Методика SMART
Методика SMART Программное обеспечение. Лекция 3
Программное обеспечение. Лекция 3 Техника LOW POLY
Техника LOW POLY Реквием по фронту. Библиотека Korolev
Реквием по фронту. Библиотека Korolev Современные модели качества программных продуктов
Современные модели качества программных продуктов