Последовательность Фибоначчи

Чи́сла Фибона́ччи — элементы числовой последовательности
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, … ,в которой первые два числа равны либо 1 и 1, либо 0 и 1, а каждое последующее число равно сумме двух предыдущих чисел. Названы в честь средневекового математика Фибоначчи.

формула

Иногда числа Фибоначчи рассматривают и для отрицательных значений как двусторонне бесконечную последовательность, удовлетворяющую тому же рекуррентному соотношению. При этом члены с отрицательными индексами легко получить с помощью эквивалентной формулы «назад»

Кто такой Фибоначчи??
Леона́рдо Пиза́нский (1170-1250) — первый крупный математик средневековой Европы. Наиболее известен под прозвищем Фибона́ччи.

Откуда взялась последовательность?
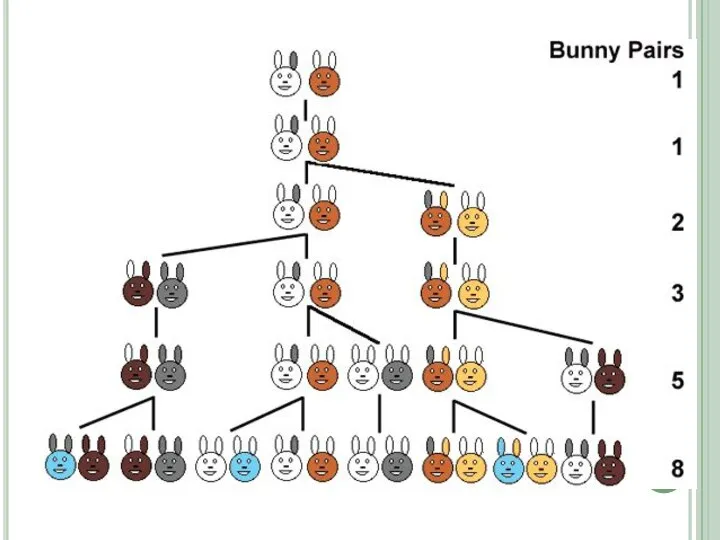
Дано: 1 пара кроликов. 1 месяц они растут. Каждый месяц они способны рождать еще по 1 паре кроликов.
Вопрос: сколько пар кроликов будет через год?

Последовательность Фибоначчи и золотое сечение.

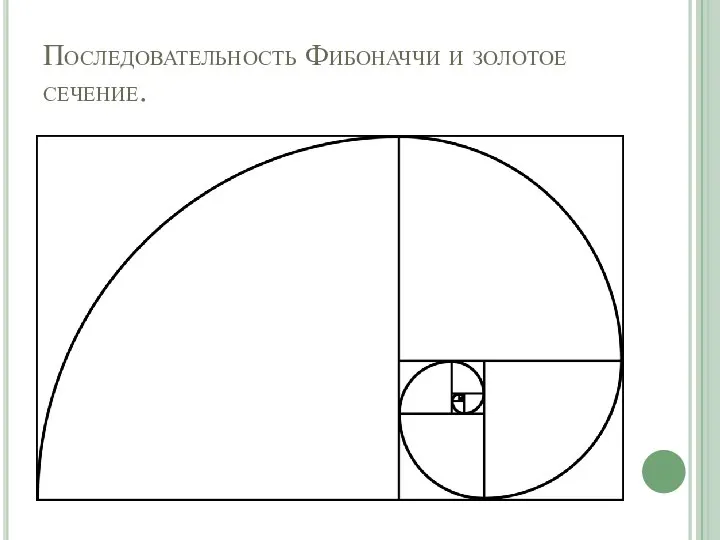
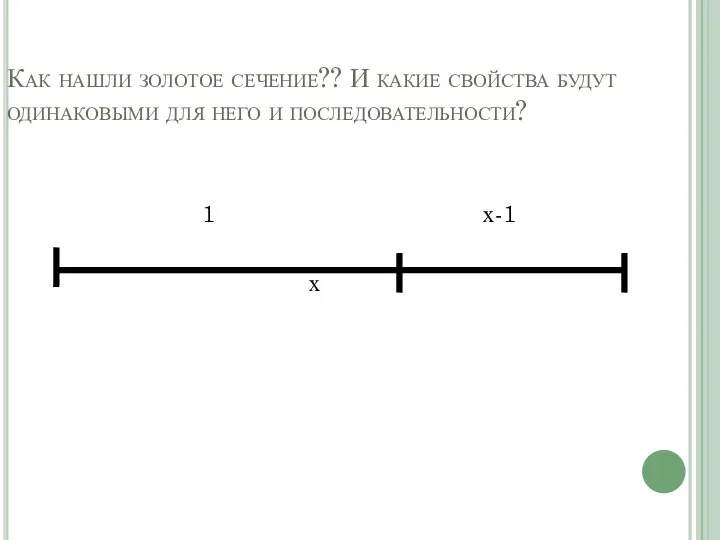
Как нашли золотое сечение?? И какие свойства будут одинаковыми для него и последовательности?
1 х-1
х

Попробуем найти сумму членов последовательности Фибоначчи
Для этого выберем любые 10 соседних чисел последовательности и просуммируем их. 1+1+2+3+5+8+13+21+34+55=143=11*13
Сумма 10 любых чисел последовательности будет кратна 11.
Удивительно, что складывать все эти числа не обязательно, тк достаточно 11 умножить на 7 член, взятый из последовательности
21+24+55+89+144+233+377+610+987+1597=4147=11*377

Еще один сюрприз?
Для любого n сумма первых n членов последовательности всегда будет равна разности (n+2)-го и первого члена последовательности. 1+1+2+3+5+8+13+21+34+55=143=(55+89)-1

головоломки? Или последовательность?
3 любых последовательных числа в последовательности ведут себя предсказуемым образом. Возьмем (3,5,8), перемножим 2 крайних, и сравним с квадратом среднего числа. Разница всегда будет в ±1.

Треугольник Паскаля

Простые числа
1,2,3,5,8,13,21…n

Последовательность Фибоначчи вокруг нас