Содержание
- 2. Перестановки Пусть задано множество из n элементов. Упорядочение этих элементов называется перестановкой. Иногда добавляют «из n
- 3. Теорема о числе перестановок Число перестановок из n элементов равно n! - произведению чисел от 1
- 4. Нумерация перестановок Чтобы нумеровать перестановки, мы отобразим множество Pn взаимнооднозначно в другое множество Tn, на котором
- 5. Отображение Возьмем перестановку и выпишем рядом с ней тривиальную перестановку. В качестве первого индекса возьмем место
- 6. Пример отображения 0 1 2 3 4 5 6 Индекс c a d f g b
- 7. Нумерация множества Tn Любое прямое произведение упорядоченных множеств можно рассматривать как систему счисления с переменным основанием.
- 8. Нумерация множества Tn - 2 Формулу #, находящую номер для набора индексов i1, i2, …, in-1,
- 9. Перебор наборов индексов Исходя из вышеизложенного, перебрать перестановки просто: нужно перебрать все наборы индексов из и
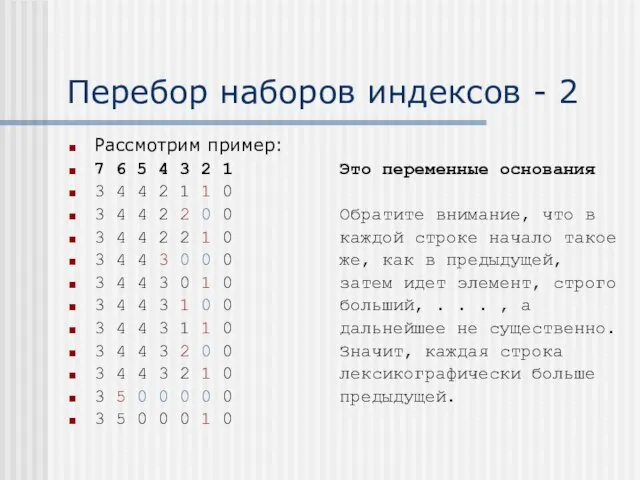
- 10. Перебор наборов индексов - 2 Рассмотрим пример: 7 6 5 4 3 2 1 Это переменные
- 11. Теорема о лексикографическом переборе перестановок Описанный алгоритм перебирает перестановки в порядке лексикографического возрастания. Доказательство. Нам достаточно
- 12. Прямой алгоритм лексикографического перебора перестановок Возьмем какую-либо перестановку p и прямо найдем лексикографически следующую. Возьмем начало
- 13. Прямой алгоритм лексикографического перебора перестановок - 2 Выпишем несколько следующих перестановок. (4, 2, 1, 7, 5,
- 14. Формальное описание алгоритма Рабочее состояние: Перестановка p и булев признак isActive. Начальное состояние: В записана тривиальная
- 15. Еще алгоритм перебора перестановок Попробуем теперь перебрать перестановки так, чтобы две последовательные перестановки мало отличались друг
- 16. Еще алгоритм перебора перестановок -2 Посмотрим пример. 1 2 3 4 5 Чей ход 1 2
- 17. Перебор перестановок. 1 function ExistsNextPerm(var kCh: integer): Boolean; var iV,iP,iVC,iPC: integer; begin result := False; for
- 18. Задача о минимуме суммы попарных произведений Пусть заданы два набора по n чисел, скажем, {ak|k∈1:n} и
- 19. Теорема о минимуме суммы попарных произведений Минимум суммы попарных произведений достигается на тривиальной перестановке. Доказательство. Предположим,
- 20. Задача о максимальной возрастающей подпоследовательности Задана последовательность {ak|k∈1:n} чисел длины n. Требуется найти ее последовательность наибольшей
- 21. Нахождение максимальной возрастающей подпоследовательности Будем по возможности экономно разбивать нашу на убывающие последовательности (пример изменен) 9
- 22. Задача о минимальном числе инверсий Задана последовательность {ak|k∈1:n} чисел длины n. Инверсией назовем выполняемое на месте
- 23. Экзаменационные вопросы Перестановки. Их перебор и нумерация. Задача о минимуме скалярного произведения. Задача о наибольшей возрастающей
- 25. Скачать презентацию





















 Человек и информация
Человек и информация Получение сведений из фонда данных государственной кадастровой оценки
Получение сведений из фонда данных государственной кадастровой оценки Организация работы локальной сети. Стек протоколов TCP/IP
Организация работы локальной сети. Стек протоколов TCP/IP Easybizzi — пакеты входа. Стоимость и комплектация
Easybizzi — пакеты входа. Стоимость и комплектация Software. Operating system
Software. Operating system Kvalitativní analýza dat
Kvalitativní analýza dat Файловые системы. Жесткие диски. FAT, EXT. Особенности ФС. LVM в Linux
Файловые системы. Жесткие диски. FAT, EXT. Особенности ФС. LVM в Linux Инструкция к обнулению ЗН и КЗ
Инструкция к обнулению ЗН и КЗ تطبيق أمانتي
تطبيق أمانتي Предзаказ
Предзаказ Настройки рабочего стола на примере Линукс Минт
Настройки рабочего стола на примере Линукс Минт Чтобы пригласить нового пользователя
Чтобы пригласить нового пользователя Каким он должен быть?
Каким он должен быть? Реализация межпредметных связей на уроках информатики
Реализация межпредметных связей на уроках информатики Введение в информатику. Основные разделы дисциплины
Введение в информатику. Основные разделы дисциплины Портал электросетевых услуг ПАО Россети
Портал электросетевых услуг ПАО Россети Основы построения моделирующего алгоритма в среде GPSS World
Основы построения моделирующего алгоритма в среде GPSS World Играть в спотах
Играть в спотах База данных (БД)
База данных (БД) Что такое алгоритм. 6 класс (1)
Что такое алгоритм. 6 класс (1) Лабораторная работа. Оформление презентации
Лабораторная работа. Оформление презентации Верстка страниц
Верстка страниц Технология OLE-Automation
Технология OLE-Automation Весенняя школа SMM
Весенняя школа SMM Как защитить ребенка от негативных факторов сети Интернет. Для родителей и учителей 4-5 класс
Как защитить ребенка от негативных факторов сети Интернет. Для родителей и учителей 4-5 класс Работа по вариантам 10 к 2 ( гугл - тест )
Работа по вариантам 10 к 2 ( гугл - тест ) Информационные ресурсы в активе учителя биологии
Информационные ресурсы в активе учителя биологии Классификация программного обеспечения
Классификация программного обеспечения