Презентация на тему Введение в теорию графов

Введение в теорию графов
Граф отображает элементный состав системы и структуру связей.

Граф - это множество точек или вершин и множество линий или ребер, соединяющих между собой все или часть этих точек.
Вершины, прилегающие к одному и тому же ребру, называются смежными. Два ребра, у которых есть общая вершина, также называются смежными (или соседними).
Рис. 1. Граф с шестью вершинами и семью ребрами
Понятие графа

Петля это дуга, начальная и конечная вершина которой совпадают.
Пустым (нулевым)называется граф без ребер.
Полным называется граф, в котором каждые две вершины смежные.
Элементы графа

Нулевой граф
Граф, состоящий из «изолированных» вершин, называется нулевым графом
Рис. 2. Нулевой граф

Неполный граф
Графы, в которых не построены все возможные ребра, называются неполными графами.
Рис. 3. Неполный граф

Степень графа
Количество рёбер, выходящих из вершины графа, называется степенью вершины. Вершина графа, имеющая нечётную степень, называется нечетной, а чётную степень – чётной.
Если степени всех вершин графа равны, то граф называется однородным. Таким образом, любой полный граф — однородный.

Заметим, что если полный граф имеет n вершин, то количество ребер равно
n(n-1)/2
Задание 1. Существует ли полный граф с семью ребрами?
Решение: Зная количество ребер, узнаем количество вершин.
n(n-1)/2=7.
n(n-1)=14.
Заметим, что n и (n-1) – это два последовательных натуральных числа. Число 14 нельзя представить
в виде произведения двух последовательных натуральных чисел, значит, данное уравнение не имеет решений. Следовательно, такого графа
не существует.
ОТВЕТ

Построить полный граф, если известно что он содержит в себе 7 вершин.
Составьте схему проведения розыгрыша кубка по олимпийской системе, в которой участвуют 10 команд.
Задание 2.

Ориентированный граф
Два ребра, у которых есть общая вершина, также называются смежными (или соседними).
Граф называется ориентированным (или орграфом), если некоторые ребра имеют направление. Это означает, что в орграфе некоторая вершина может быть соединена с другой вершиной, а обратного соединения нет. Если ребра ориентированы, что обычно показывают стрелками, то они называются дугами.
Рис. 4. Ориентированный граф

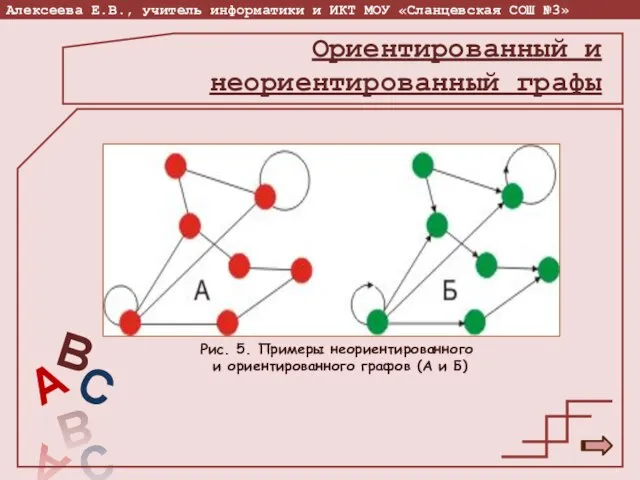
Рис. 5. Примеры неориентированного
и ориентированного графов (А и Б)
Ориентированный и неориентированный графы

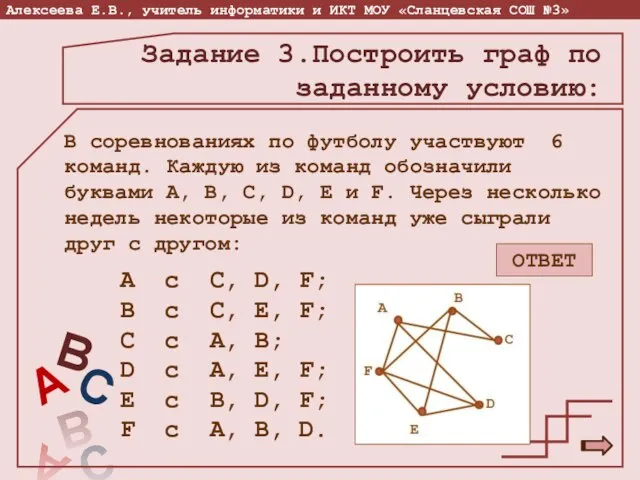
Задание 3.Построить граф по заданному условию:
В соревнованиях по футболу участвуют 6 команд. Каждую из команд обозначили буквами А, B, C, D, E и F. Через несколько недель некоторые из команд уже сыграли друг с другом:
A с C, D, F;
B c C, E, F;
С с A, B;
D с A, E, F;
E с B, D, F;
F с A, B, D.
ОТВЕТ

Не следует путать изображение графа с собственно графом (абстрактной структурой), поскольку одному графу можно сопоставить не одно графическое представление. Изображение призвано лишь показать, какие пары вершин соединены рёбрами, а какие — нет.
Запомнить!

Изображение графа
Один и тот же граф может выглядеть на
рисунках по-разному. На рисунке 6 (а, б, в) изображен один и тот же граф.
Рис. 6. Примеры изображения графа

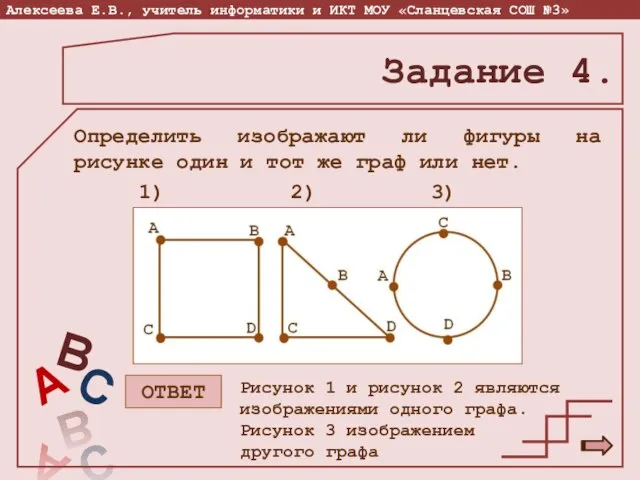
Задание 4.
Определить изображают ли фигуры на рисунке один и тот же граф или нет.
1)
2)
3)
ОТВЕТ
Рисунок 1 и рисунок 2 являются изображениями одного графа. Рисунок 3 изображением
другого графа

Путём в графе называется такая последовательность ребер, в которой каждые два соседних ребра имеют общую вершину и никакое ребро не встречается более одного раза.
Путь в графе

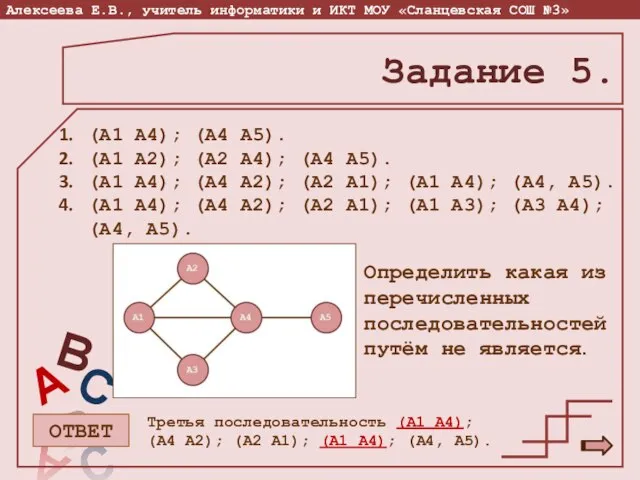
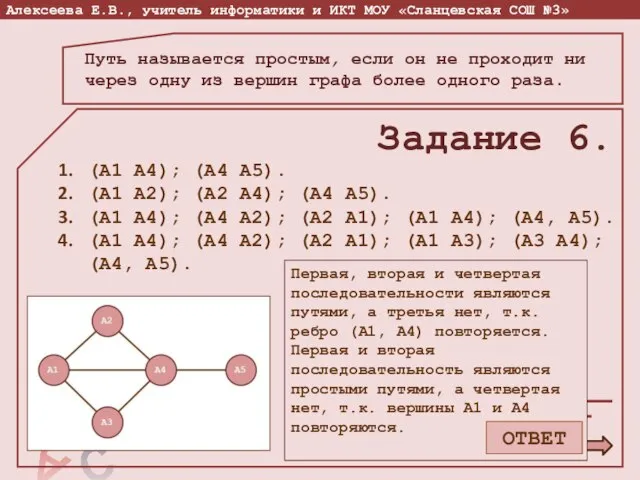
Задание 5.
(А1 А4); (А4 А5).
(А1 А2); (А2 А4); (А4 А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А3); (А3 А4); (А4, А5).
Определить какая из перечисленных последовательностей путём не является.
ОТВЕТ
Третья последовательность (А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).

Путь называется простым, если он не проходит ни через одну из вершин графа более одного раза.
(А1 А4); (А4 А5).
(А1 А2); (А2 А4); (А4 А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А4); (А4, А5).
(А1 А4); (А4 А2); (А2 А1); (А1 А3); (А3 А4); (А4, А5).
Задание 6.
Определите, какие последовательности ребер являются путями, и какие из них простые. Если последовательность не является путем укажите почему.
Первая, вторая и четвертая последовательности являются путями, а третья нет, т.к. ребро (А1, А4) повторяется.
Первая и вторая последовательность являются простыми путями, а четвертая нет, т.к. вершины А1 и А4 повторяются.
ОТВЕТ

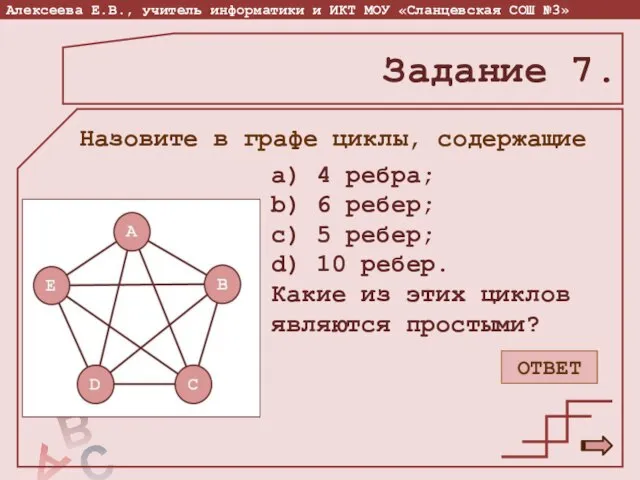
Понятие цикла в графе
Циклом называется путь, в котором совпадают его начальная и конечная вершины.
Простым циклом в графе называется цикл, не проходящий ни через одну из вершин графа более одного раза.

a) 4 ребра;
b) 6 ребер;
c) 5 ребер;
d) 10 ребер. Какие из этих циклов являются простыми?
Задание 7.
Назовите в графе циклы, содержащие
ОТВЕТ