Содержание
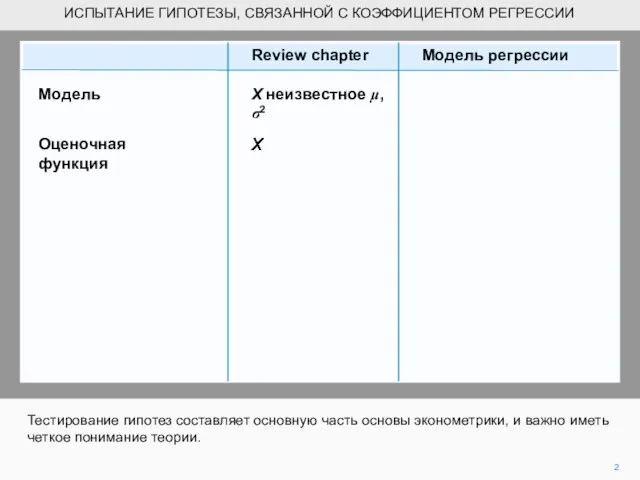
- 2. ИСПЫТАНИЕ ГИПОТЕЗЫ, СВЯЗАННОЙ С КОЭФФИЦИЕНТОМ РЕГРЕССИИ Тестирование гипотез составляет основную часть основы эконометрики, и важно иметь
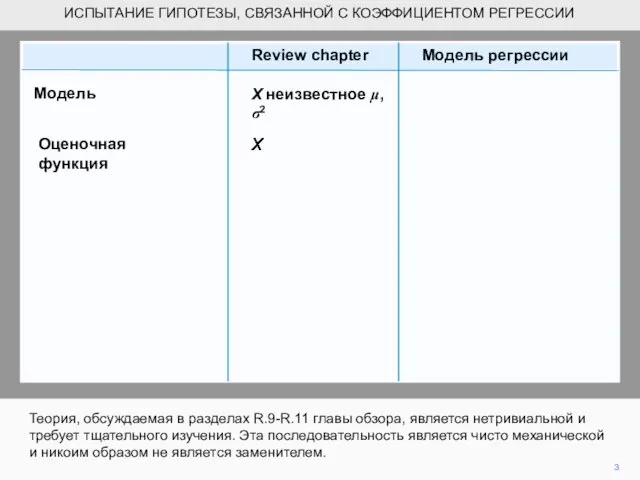
- 3. ИСПЫТАНИЕ ГИПОТЕЗЫ, СВЯЗАННОЙ С КОЭФФИЦИЕНТОМ РЕГРЕССИИ Теория, обсуждаемая в разделах R.9-R.11 главы обзора, является нетривиальной и
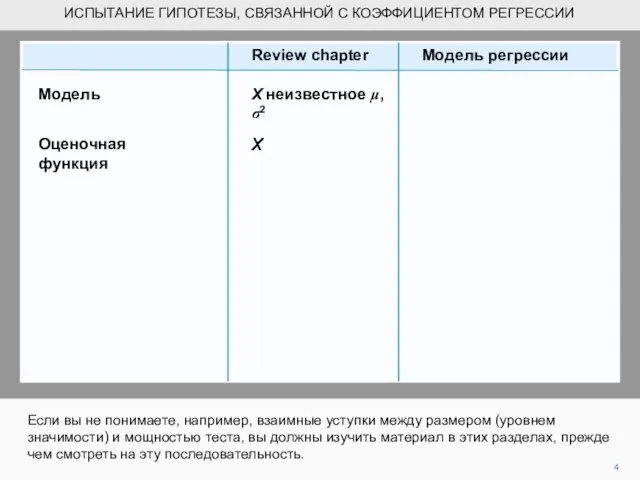
- 4. ИСПЫТАНИЕ ГИПОТЕЗЫ, СВЯЗАННОЙ С КОЭФФИЦИЕНТОМ РЕГРЕССИИ Если вы не понимаете, например, взаимные уступки между размером (уровнем
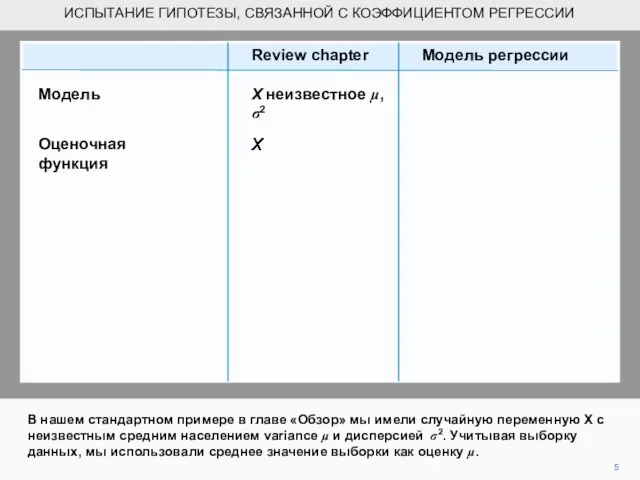
- 5. В нашем стандартном примере в главе «Обзор» мы имели случайную переменную Х с неизвестным средним населением
- 6. В контексте модели регрессии мы имеем параметры β1 и β2 и для них были получены оценки
- 7. В случае случайной величины X, наша стандартная нулевая гипотеза заключалась в том, что μ было равно
- 8. Для обеих популяций среднее значение μ случайной величины X и коэффициент регрессии β2, тестовая статистика является
- 9. В обоих случаях он определяется как разница между расчетным коэффициентом и его гипотетическим значением, деленная на
- 10. Мы отклоняем нулевую гипотезу, если абсолютное значение больше критического значения t, учитывая выбранный уровень значимости. 10
- 11. Есть одно важное различие. При определении критического значения t необходимо учитывать число степеней свободы. В случае
- 12. Статистика испытаний В случае модели регрессии число степеней свободы n - k, где n - количество
- 13. 13 В качестве иллюстрации мы рассмотрим модель, связанную с инфляцией цен для инфляции заработной платы. p
- 14. 14 Мы проверим гипотезу о том, что темп инфляции цен равен ставке инфляции заработной платы. Поэтому
- 15. 15 Предположим, что результат регрессии показан (стандартные ошибки в скобках). Наша фактическая оценка коэффициента наклона составляет
- 16. 16 Мы вычисляем t статистику путем вычитания гипотетического истинного значения из оценки выборки и деления на
- 17. 17 В выборке имеется 20 наблюдений. Мы оценили 2 параметра, поэтому существует 18 степеней свободы. ИСПЫТАНИЕ
- 18. 18 Критическое значение t с 18 степенями свободы составляет 2,101 на уровне 5%. Абсолютное значение t-статистики
- 19. 19 На практике обычно не имеют представление о фактическом значении коэффициентов. Очень часто цель анализа состоит
- 20. 20 В этом случае обычно определяется β2 = 0 как нулевая гипотеза. На словах нулевая гипотеза
- 21. 21 For the null hypothesis β2 = 0, the t statistic reduces to the estimate of
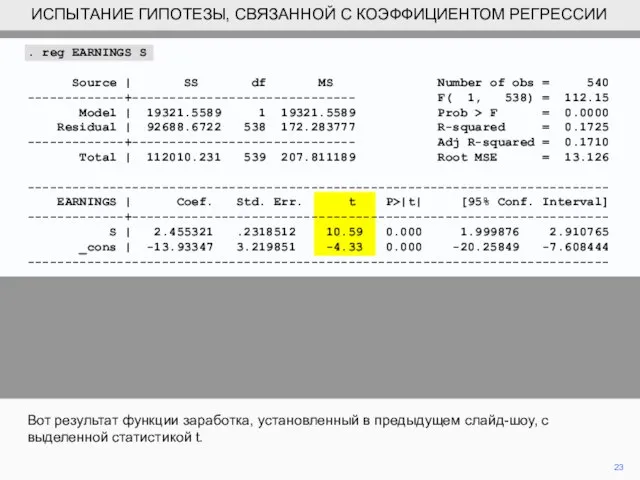
- 22. 22 Это отношение обычно называют t статистикой для коэффициента и автоматически распечатывается как часть результатов регрессии.
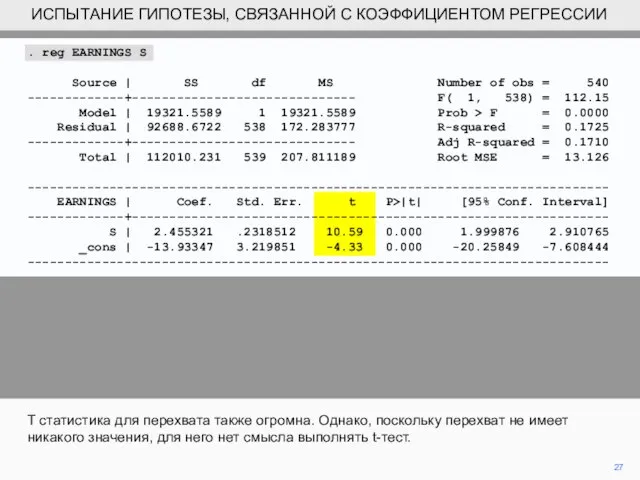
- 23. . reg EARNINGS S Source | SS df MS Number of obs = 540 -------------+------------------------------ F(
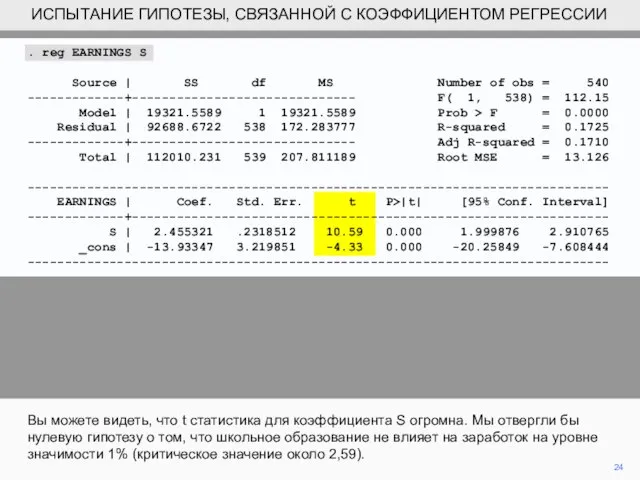
- 24. 24 Вы можете видеть, что t статистика для коэффициента S огромна. Мы отвергли бы нулевую гипотезу
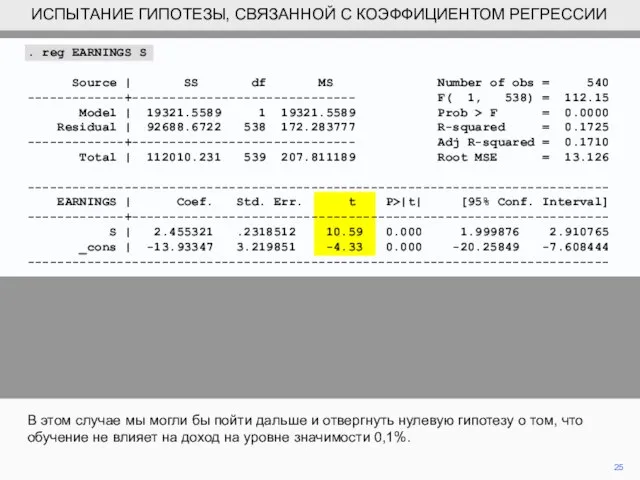
- 25. 25 В этом случае мы могли бы пойти дальше и отвергнуть нулевую гипотезу о том, что
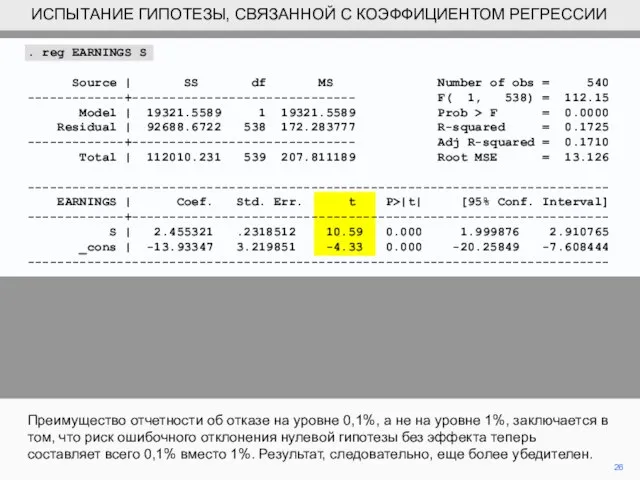
- 26. 26 Преимущество отчетности об отказе на уровне 0,1%, а не на уровне 1%, заключается в том,
- 27. 27 T cтатистика для перехвата также огромна. Однако, поскольку перехват не имеет никакого значения, для него
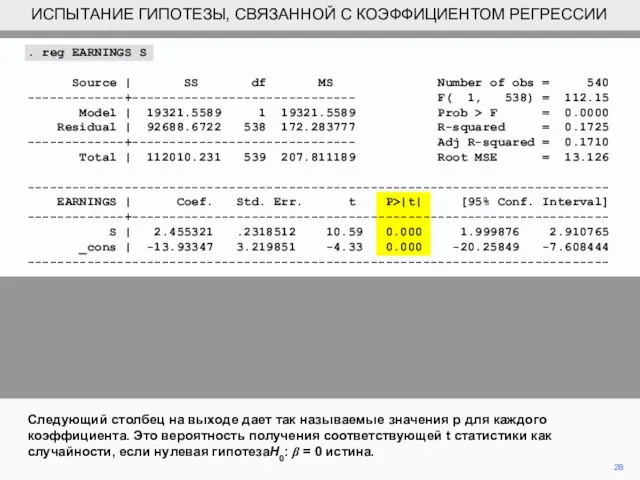
- 28. 28 Следующий столбец на выходе дает так называемые значения р для каждого коэффициента. Это вероятность получения
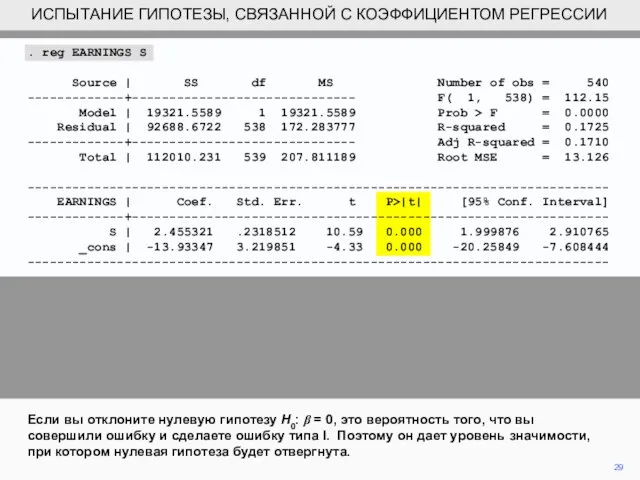
- 29. 29 Если вы отклоните нулевую гипотезу H0: β = 0, это вероятность того, что вы совершили
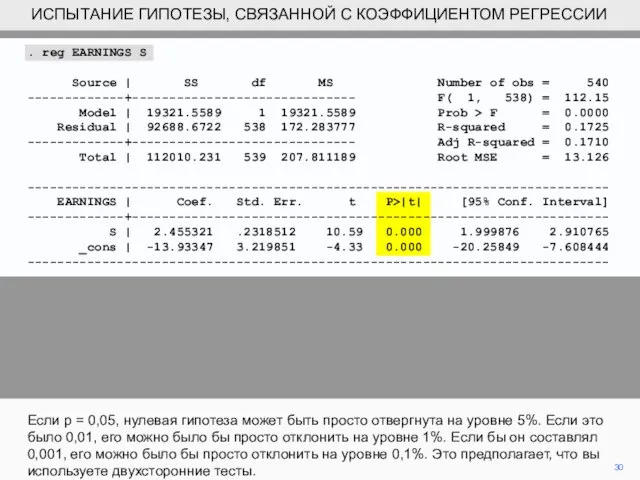
- 30. 30 Если p = 0,05, нулевая гипотеза может быть просто отвергнута на уровне 5%. Если это
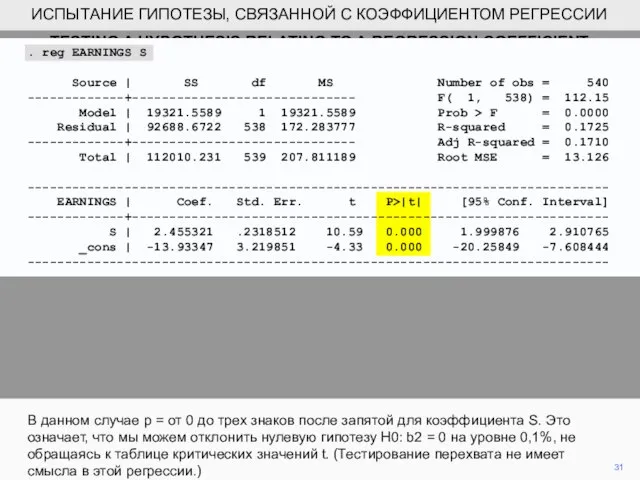
- 31. 31 В данном случае p = от 0 до трех знаков после запятой для коэффициента S.
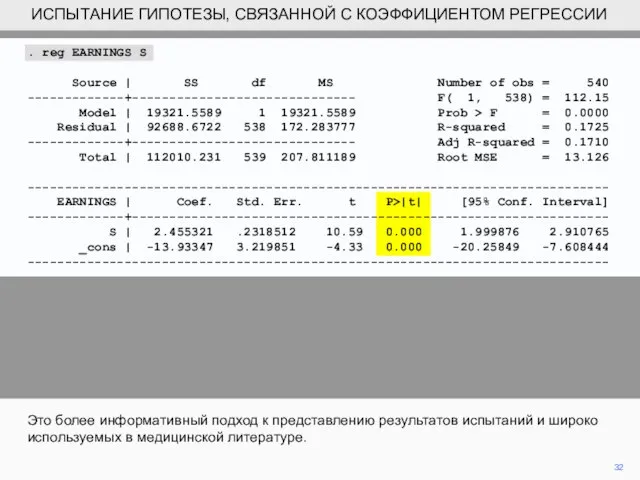
- 32. 32 Это более информативный подход к представлению результатов испытаний и широко используемых в медицинской литературе. ИСПЫТАНИЕ
- 34. Скачать презентацию

















 Знакомство с системой компьютерной математики
Знакомство с системой компьютерной математики Операционные системы
Операционные системы Управление программным обеспечением
Управление программным обеспечением Poddotazy
Poddotazy Как создать страницу компании в Google
Как создать страницу компании в Google Форматирование текста (шрифт 2). Web-проектирование
Форматирование текста (шрифт 2). Web-проектирование Формулы, применяющиеся в Excel
Формулы, применяющиеся в Excel Моделирование — это метод познания, состоящий в создании и исследовании моделей
Моделирование — это метод познания, состоящий в создании и исследовании моделей Интерактивный путеводитель
Интерактивный путеводитель Препятствия диджитализации страхования в России и возможные пути их преодоления
Препятствия диджитализации страхования в России и возможные пути их преодоления Linux – маршрутизация, NAT, DHCP
Linux – маршрутизация, NAT, DHCP Programming on Python. Lecture 7
Programming on Python. Lecture 7 Котельная Спортлагерь Олимп
Котельная Спортлагерь Олимп Администратор баз данных областное автономное учреждение социального обслуживания
Администратор баз данных областное автономное учреждение социального обслуживания Скандальные домены
Скандальные домены Описательные статистики
Описательные статистики Microservices and monolith
Microservices and monolith Диалоги в поселке
Диалоги в поселке Жизненный цикл информационной системы
Жизненный цикл информационной системы 6-12-1-grafiki-i-diagrammy
6-12-1-grafiki-i-diagrammy Массивы
Массивы Информационно-коммуникационные технологии обучения (ИКТ)
Информационно-коммуникационные технологии обучения (ИКТ) Видеотехнологии. Кодирование видео (теория)
Видеотехнологии. Кодирование видео (теория) programmirovanie_l5-2016
programmirovanie_l5-2016 Пэкмен. Обзор. Скайрим – моя жизнь
Пэкмен. Обзор. Скайрим – моя жизнь Принцип программного управления компьютером. Лекция № 2
Принцип программного управления компьютером. Лекция № 2 Основы языка Visual Basic. Функции
Основы языка Visual Basic. Функции Хронометраж для соревнований
Хронометраж для соревнований