Раскраска граней многоугольных графов

Алгоритм действий в графическом окне
В начале выполнения программы графическое окно должно быть занимать четверть площади экрана в его центре, а все грани изображения графа в нем должны иметь одинаковый цвет фона.
Изменение цвета каждой грани должно осуществляться по щелчку любой кнопки мыши, когда ее курсор находится внутри грани. Для раскраски граней в программе должна быть распределена палитра из n=4 различных цветов (плюс еще один цвет для изображения вершин и ребер).
Чтобы установить необходимый цвет для любой грани в программе должен быть реализован циклический перебор цветов палитры с перекраской указанной грани последовательно в каждый из них по щелчку любой кнопки мыши. Кроме того, следует предусмотреть перезагрузку изображения графа с перекраской в одинаковый фоновый цвет всех граней по нажатию клавиши ESC на клавиатуре, а также принудительную перерисовку графического окна по нажатию комбинации клавиш ALT-ESC с сохранением раскраски граней.
Завершение программы должно происходить по нажатию клавиши F10 клавиатуре. При разработке программы должна быть реализована обработка соответствующих событий и изображений в ее графическом окне с многоугольными регионами для граней графа. Для этого следует применить библиотечные функции базового программного интерфейса X Window System. При выполнении программы требуется построить правильную раскраску граней заданной фигуры многоугольного графа минимальным числом цветов, когда все смежные грани имеют различные цвета.
Для интерактивной раскраски различных многоугольных графов могут быть разработаны функционально идентичные программы. Все они будут различаться только по коду пары конфигурационных функций с координатными и структурными данными, которые допускают техническую переделку по шаблону.

Программа для раскраски графа пирамиды
граф пирамиды имеет 5 вершин, 8 ребер, 4 внутренние 3-угольные боковые грани и 4-угольное основание внешней грани. Плоская укладка многоугольного графа пирамиды показана на следующей схеме в координатной сетке из (8х8) клеток с произвольной нумерацией вершин его вершин, где RGB литеры граней обозначают цвета их правильной раскраски:
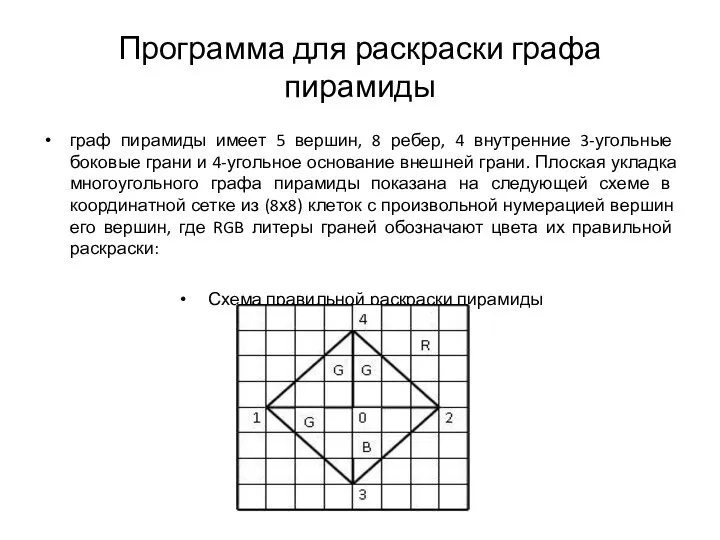
Схема правильной раскраски пирамиды

Структура программы раскраски графа
Исходный текст этой программы раскраски графа целесообразно разделить на 3 модуля из геометрических, дисплейных и контролирующих прикладных функций. Декларации их информационных структур и макроопределение их констант следует сосредоточить в заголовочном файле "polyhedron.h", который включается в каждый функциональный модуль директивой include. Он начинается подключением системных заголовков базового интерфейса и утилит X-графики следующими директивами:
#include
#include
Для вершин и ребер используются типовые графические структуры XPoint и XSegment , которые переименовываются в XVertex и XEdge следующими директивами:
typedef XPoint XVertex; /* Структура вершины */
typedef XSegment XEdge; /* Структура ребра */

Структура многоугольного графа
Для спецификации граней многоугольного графа декларируется следующая собственная структура XFace:
typedef struct { /* Структура грани */
XPoint *top; /* Адрес набора вершин */
int Cn; /* Число вершин */
int tone; /* Номер цвета */
Region zone; /* Региональная зона */
}XFace;
Геометрическую модель многоугольного графа, в которой адресованы его перечисленные компоненты, декларирует следующая программная структура XPolyGraph:
typedef struct { /* Структура многоугольного графа */
XVertex* vertex; /* Адрес массива вершин */
XEdge* edge; /* Адрес массива ребер */
XFace* face; /* Адрес массива граней */
} XPolyGraph;

Поля структуры XPolyGraph
Поля структуры XPolyGraph предназначены для адресации одноименных статических массивов геометрического модуля. Их размеры фиксируют число вершин, ребер и внутренних граней (плюс одна внешняя грань) на схеме графа макросами NVERT, NEDGE и NFACE, которые вычисляются в заголовочном файле. Этим вычислениям предшествует макроопределение константы MB0 для числа вершин внешней грани и констант NFm, каждая из которых фиксирует число m-угольных внутренних граней по схеме графа, причем, обычно 3
#define MB0 4 /* 4-угольная внешняя грань */
#define NF3 4 /* 4 3-угольные внутренние грани */
/* #define NF4 0 */ /* 0 4-угольных внутренних граней */
/* #define NF5 0 */ /* 0 5-угольных внутренних граней */
/* #define NF6 0 */ /* 0 6-угольных внутренних граней */
/* #define NF7 0 */ /* 0 7-угольных внутренних граней */
/* #define NF8 0 */ /* 0 8-угольных внутренних граней */

Расчет значений угольных констант для других графов
Для других графов эти значения угольных констант должны быть изменены, но в любом варианте они обеспечивают конструктивное определение числа вершин, ребер и граней по соотношениям многоугольных графов. Проще всего найти число внутренних граней NFACE. Его определяет сумма внутренних угольников плоской укладки. Для графа пирамиды в этой сумме остаются только NF3 3-угольников и макроопределение числа граней имеет вид:
#define NFACE (NF3) /* (NF3+ NF4+ NF5 \
+ NF6+ NF7+NF8) */
Число ребер NEDGE любого многоугольника графа определяет половина суммарной угольности граней. Для пирамиды вместе с угольностью внешней грани MB0 учитываются опять только NF3 3-угольников. Поэтому макроопределение числа ребер имеет следующий вид, а комментарий показывает расчетную формулу для общего случая:
#define NEDGE ((3*NF3 + MB0)/2) /* ((3*NF3 + 4*NF4 \
+ 5*NF5 + 6*NF6 \
+ 7*NF7 + 8*NF8 \
+ MB0)/2) */
Число ребер, согласно формуле Эйлера для любого плоского графа, на два меньше суммы числа вершин и граней (с учетом внешней грани). Вычисление числа вершин NVERT по Эйлеру обеспечивает следующее макроопределение:
#define NVERT (NEDGE-(NFACE+1)+2) /* V+F−E=2 */

Макроопределения инвариантных констант, не зависящих от структуры графа
Кроме указанных топологических констант графа, заголовочный файл содержит следующие макроопределения инвариантных констант, которые не зависят от структуры графа:
#define NTONE 4 /* число цветов граней графа */
#define DEFTONE 0 /* номер цвета грани по умолчанию */
#define VDOT 8 /* диаметр вершин графа */
#define EWIDTH 2 /* толщина ребер графа (
#define NUNIT 8 /* диапазон градуировка схемы %8=0*/

Спецификация прототипов всех прикладных функций с разделением их по модулям
Многогранный заголовочный файл завершает спецификация прототипов всех прикладных функций с разделением их по модулям:
/*Геометрический модуль (pyramid1) */
int assoc(XPolyGraph*);
GC congraph(Display*);
Window wingraph(Display*, char*);
int colorite(Display*);
int regraph(Display*, Window, GC, int);
int reset(Display*, Window, int);
int reface(Display*, Window, GC, int);
/*Дисплейный модуль (pyramid2) */
int relink(XPolyGraph*);
int retrace();
int resize(unsigned, unsigned);
int rescale(unsigned, unsigned);
int rebuild();
int reconf(unsigned, unsigned);
int zotone(int, int);
/*Контрольный модуль (pyramid0) */
int rekey(XEvent*);
int dispatch(Display*, Window, GC);
int main(int, char* argv[]);

Структура геометрического модуля
В геометрический модуль входят 7 прикладных функций для формирования и обработки геометрической модели многоугольного графа по его программной структуре XPolyGraph. Их информационную связь обеспечивают внешние статические массивы и структуры. Исходный код модуля начинает подключение многоугольного заголовка графа следующей директивой:
#include "polyhedron.h"
После заголовка вводятся следующие статические массивы структур вершин, ребер и граней графа для их адресации в одноименных полях его структуры XPolyGraph:
static XVertex vertex[NVERT]; /* массив вершин */
static XEdge edge[NEDGE]; /* массив ребер */
static XFace face[(NFACE+1)]; /* массив граней */
Эти массивы образуют инвариантную часть геометрической модели графа, которая не зависит от его топологии. Их требуется дополнить координатными массивами вершин равноугольных граней, набор и размер которых определяет конфигурация многоугольного графа. Для графа пирамиды, который имеет только NF3=4 (боковые) 3-угольные внутренние грани, определяется следующий массив для пар координат их вершин:
static XPoint face3[NF3][(3+1)];

Задание координатных массивов вершин равноугольных граней
Ряды пар координат вершин каждой грани этого массива адресуются (топовыми) полями (top) структуры граней XFace и составляют топозависимую часть геометрической модели графа, которую определяет его топология и конфигурация. Для любого заданного графа нужно заявить аналогичные координатные массивы его m-угольных граней (3
/* static XPoint face4[NF4][(4+1)]; */
/* static XPoint face5[NF4][(4+1)]; */
/* static XPoint face6[NF4][(4+1)]; */
/* static XPoint face7[NF4][(4+1)]; */
/* static XPoint face8[NF8][(8+1)]; */
Сегмент внешних статических данных геометрического модуля завершает декларация измерительной структуры для установки масштаба графа по горизонтали и вертикали, который зависит от размеров окна программы. Соответствующие коэффициенты масштабирования задают размеры клеток градуировки схемы графа в пикселях графического окна полями следующей внешней графической структуры:
static XPoint scale; /*структура масштаба по Х и Y */
Ряды пар координат вершин каждой грани этого массива адресуются (топовыми) полями (top) структуры граней XFace и составляют топозависимую часть геометрической модели графа, которую определяет его топология и конфигурация.

Координатные массивы его m-угольных граней (3
Для любого заданного графа нужно заявить аналогичные координатные массивы его m-угольных граней (3
/* static XPoint face4[NF4][(4+1)]; */
/* static XPoint face5[NF4][(4+1)]; */
/* static XPoint face6[NF4][(4+1)]; */
/* static XPoint face7[NF4][(4+1)]; */
/* static XPoint face8[NF8][(8+1)]; */
Сегмент внешних статических данных геометрического модуля завершает декларация измерительной структуры для установки масштаба графа по горизонтали и вертикали, который зависит от размеров окна программы. Соответствующие коэффициенты масштабирования задают размеры клеток градуировки схемы графа в пикселях графического окна полями следующей внешней графической структуры:
static XPoint scale; /*структура масштаба по Х и Y */
(3
/* static XPoint face4[NF4][(4+1)]; */
/* static XPoint face5[NF4][(4+1)]; */
/* static XPoint face6[NF4][(4+1)]; */
/* static XPoint face7[NF4][(4+1)]; */
/* static XPoint face8[NF8][(8+1)]; */
Сегмент внешних статических данных геометрического модуля завершает декларация измерительной структуры для установки масштаба графа по горизонтали и вертикали, который зависит от размеров окна программы. Соответствующие коэффициенты масштабирования задают размеры клеток градуировки схемы графа в пикселях графического окна полями следующей внешней графической структуры:
static XPoint scale; /*структура масштаба по Х и Y */

Функциональный блок геометрического модуля. Прикладная функция assoc
Функциональный блок геометрического модуля начинается с прикладной функции assoc. Ее первой вызывает основная функция main, чтобы ассоциировать поля вершин, ребер и граней структуры графа XРolyGraph c одноименными статическими массивами геометрического модуля. Такая ассоциация обеспечивает распределение статической памяти программы для геометрической модели графа, адрес структуры которой передается в функцию assoc. Исходный код функции assoc имеет следующий вид.
/* Модельная ассоциация структуры полиграфа */
int assoc(XPolyGraph* pg) {
pg->vertex = vertex; /* адресация массива вершин */
pg->edge = edge; /* адресация массива ребер */
pg->face = face; /* адресация массива граней */
retrace(); /* трассировка граней /*
return(0);
} /* assoc */
После ассоциации адресов функция assoc вызывается функцию retrace, которая обеспечивает трассировку массива граней геометрической модели графа XPolyGraph для инициализации полей их структур XFace. При этом в top-поля указанных структур адресуются статические массивы для координат вершин внутренних равноугольных граней как face3 у графа пирамиды.

Трассировка рав(з)ноугольных граней в 1 массив
В общем случае исходный код функции трассировки retrace образует набор циклов адресации и инициализации для всех равноугольных граней со сквозной индексацией их номеров i в порядке роста числа их вершин. Для графа пирамиды, в частности, требуется только один цикл по 3-угольным граням.
/* КОД ФУНКЦИИ ЗАВИСИТ ОТ ГРАФА */
int retrace() {
int i=0; /* сквозной индекс разноугольных граней */
int j; /* индекс равноугольных граней */
for(j = 0; j
face[i].top = face3[j]; /* адрес массива вершин */
face[i].Cn = 3; /* число вершин грани=3 */
face[i].tone = DEFTONE; /* цветной индекс грани */
face[i].zone = XCreateRegion(); /* пустой регион */
} /* face3 */
/* for(j = 0; j < NFm; j++, i++) { ... } */ /* для m>3 */
face[i].tone = DEFTONE; /* цвет внешней грани */
return(0);
} /* retrace */
Вычисление и заполнение координатных данных во всех полях структуры XPolyGraph геометрической модели графа осуществляет функция rebuild. Она вызывается из функции reconf при отработке габаритных реконфигураций графического окна. Для пересчета координат функция rebuild использует свои внутренние статические массивы, которые кодируют конфигурацию вершин, ребер и равноугольных граней по заданной схеме графа.

Перестройка модельной геометрии графа
/* КОД ФУНКЦИИ ЗАВИСИТ ОТ ГРАФА */
int rebuild() {
static XPoint vconf[] = { /* Конфигурация вершин */
{4, 4}, {1, 4}, {7, 4}, {4, 7}, {4, 1} /* схеме пирамиды */
}; /* vconf */
static int fconf3[NF3][(3+1)] = { /* Циклические */
{0, 4, 2, 0}, /* индексы вершин для */
{0, 1, 4, 0}, /* 3-угольных граней пирамиды */
{0, 3, 1, 0},
{0, 2, 3, 0}
}; /* fconf3 */
/* static int fconfM[NF4][(4+1)] = { ... }; */
/* … координатные массивы [4−8]-угольных граней */
/* static int fconf8[NF8][(8+1)] = { ... }; */
static int econf[NEDGE][2] = { /* Пары вершин ребер: */
{0, 1}, {0, 2}, {0, 3}, {0, 4}, /* инцидентные V0 */
{1, 3}, {1, 4}, /* инцидентные V1 */
{2, 3}, {2, 4} /* инцидентные V2 */
}; /* edge */
int i, j; /* индексы вершин, ребер и граней */
for(i = 0; i < NVERT; i++) { /* Расчет оконных */
vertex[i].x = scale.x * vconf[i].x; /* координат */
vertex[i].y = scale.y * vconf[i].y; /* вершин */
} /* for-vertex */
for(i = 0; i < NEDGE; i++) { /* Фиксировать оконные */
edge[i].x1 = vertex[econf[i][0]].x; /* координаты */
edge[i].y1 = vertex[econf[i][0]].y; /* пар вершин */
edge[i].x2 = vertex[econf[i][1]].x; ; /*всех ребер */
edge[i].y2 = vertex[econf[i][1]].y;
} /* for-edge */
for(i = 0; i < NF3; i++) /* Фиксировать оконные */
for(j = 0; j < (3+1); j++) { /* координаты вершин */
face3[i][j].x = vertex[fconf3[i][j]].x; /* 3-угольных */
face3[i][j].y = vertex[fconf3[i][j]].y; /* граней */
} /* for 3-top face */
/* for(i = 0; i < NFM; i++) */ /* для M>3 */
/* for(j = 0; j < (M+1); j++) { … } */
return(0);
} /* rebuild */

Исходный текст функции rescale
Рассмотренная функция rebuild вызывается при изменении коэффициентов масштабирования изображения графа в окне программы. Их значения вычисляет функция rescale по габаритам окна в своих аргументах и числу делений градуировки схемы графа NUNIT. Результаты вычислений фиксируют поля масштабной структуры scale. Код возврата функции rescale позволяет контролировать наличие изменений масштаба. Если масштаб изменился, возвращается число граней NFACE. Возврат 0 означает сохранение масштаба при малых изменениях габаритов окна.
/* Контроль масштаба изображения */
int rescale(unsigned w, unsigned h) {
int x, y; /* коэффициенты масштабирования по x и y */
x = w / NUNIT; y = h / NUNIT; /* пересчет масштаба */
if((scale.x == x) && (scale.y == y))
return(0); /* код сохранения масштаба */
scale.x = x; scale.y = y; /* запомнить масштаб */
return(NFACE); /* код изменения масштаба */
} /* rescale */
Вычисление масштаба функцией rescale имеет смысл, когда изменяются габариты окна графа. Габаритный контроль окна выполняет функция resize, которой передаются его текущие размеры для сравнения с их прошлыми значениями в ее BAK-структуре.

Габаритный контроль окна выполняет функция resize
Функция resize запоминает габариты окна из своих аргументов и завершается с кодом числа граней NFACE. Исходный текст функции resize имеет вид.
/* Контроль изменения размеров окна */
int resize(unsigned w, unsigned h) {
static XRectangle bak = {0, 0, 0, 0 }; /* прошлые размеры */
if((bak.width == w) && (bak.height == h))
return(0); /* код сохранения размеров окна */
bak.width = w; bak.height = h; /* запомнить размеры */
return(NFACE); /* код изменения размеров окна */
} /* resize */
Комплексное использование функций resize, rescale и rebuild обеспечивает функция reconf. Ее вызывает диспетчер событий для обработки реконфигурации окна при изменении его размеров. Их текущие значения передаются в функцию reconf парой ее аргументов для контроля изменения размеров окна и масштаба изображения функциями resize и rescale. При их ненулевом возврате вызывается функция rebuild, которая модифицирует геометрическую модель графа для последующей перерисовки его изображения. В любом случае код возврата функции reconf определяется возвратом функции resize и используется для оптимизации серийных перерисовок графа. Исходный текст функции reconf имеет следующий вид.

Исходный текст функции reconf
/* Реконфигурация графа */
int reconf(unsigned w, unsigned h) {
if(resize(w, h) == 0) /* Габаритный контроль */
return(0);
if(rescale(w, h) != 0) /* Контроль масштаба */
rebuild(); /* Перестройка геометрии графа */
return(NFACE);
} /* reconf */
Геометрический модуль завершает функция zotone, которую вызывает диспетчер событий при выборе грани курсором мыши с целью перекраски в другой цвет.
Начальный блок функции zotone обеспечивает реформацию регионов всех внутренних граней по top-массивам координат их вершин последовательными запросами XDestroyRegion и XPolygonRegion, если был изменен масштаб изображения. Контроль масштаба по его структуре scale и внутренним BAK-данным реализован как в функции resize. Когда scale- и BAK-структуры совпадают по полям, регионы не изменяются. В любом случае, во втором блоке осуществляется региональный поиск грани по координатам ее внутренней точки, которые заданы аргументами функции zotone. Номер этой грани определяется по запросу XPointInRegion для полей zone регионов всех внутренних граней или равен NFACE для внешней грани. Конечный блок изменяет цветное поле tone этой грани, устанавливая для него следующее значение в циклическом порядке индексов цветов. Номер грани передает код возврата функции zotone для последующей ее перекраски в установленный цвет функцией reface. Исходный текст рассмотренной функции zotone имеет вид.

(X, Y)-идентификация грани для перекраски
int zotone(int x, int y) {
static XPoint bak = {0, 0}; /* прошлый масштаб */
int f = 0; /* индекс грани */
if((bak.x == scale.x) && (bak.y == scale.y)) /* Контроль */
f = NFACE; /* изменений масштаба изображения */
for( ; f < NFACE; f++) { /* Перестройка регионов граней */
XDestroyRegion(face[f].zone);
face[f].zone = XPolygonRegion(face[f].top, face[f].Cn, 0);
} /* for */
bak.x = scale.x; bak.y = scale.y; /* запомнить масштаб */
for(f = 0; f < NFACE; f++) /* поиск грани по точке внутри */
if(XPointInRegion(face[f].zone, x, y) == True)
break;
face[f].tone = (face[f].tone + 1) % NTONE; /* новый цвет */
return(f); /* возврат индекса грани для перекраски */
} /* zotone */
рассмотренный исходный код геометрического модуля зависит от конфигурации заданного графа и должен быть частично модифицирован. В частности, в сегмент данных требуется добавить (раскомментарить) декларации необходимых внешних статических массивов M-угольных граней faceM. В исходном коде функции retrace необходимо ввести циклы инициализации полей структур M-угольных граней. В функции rebuild нужно заполнить по схеме графа статические данные конфигурационных массивов вершин vconf и ребер econf. Кроме того, следует ввести и заполнить соответствующий набор массивов конфигурации fconfM всех M-угольных граней. Наконец, нужно добавить циклы заполнения координатных массивов M-угольных граней faceM по их конфигурационным эквивалентам fconfM в формате заполнения такого массива face3 по fconf3 для пирамиды. Других графозависимых изменений в геометрическом модуле, а также в остальных модулях программы нет.

Дисплейный модуль
В него входят 7 инвариантных функций, которые обеспечивают отображение многоугольного графа любой конфигурации в графическом окне программы, а также внешние статические переменные для их информационной связи. Исходный код дисплейного модуля начинается с подключения заголовка многоугольного графа следующей директивой:
#include "polyhedron.h"
Затем декларируются следующие адресные внешние переменные для общего доступа дисплейных функций к массивам вершин, ребер и граней геометрической модели графа, а также для палитры кодов цветов их изображения:
static XVertex *vertex; /* адрес массива вершин */
static XEdge *edge; /* адрес массиваребер */
static XFace *face; /* адрес массива граней */
static unsigned long palette[(NTONE+1)]; /* коды цветов */
Статические адреса vertex, edge и face являются косметическими алиасами одноименных адресных полей модельной структуры графа XPolyGraph, которые введены для удобства доступа. Инициализацию их значений обеспечивает функция relink, которую вызывает основная функция main для адресации структуры геометрической модели графа XPolyGraph в дисплейный модуль. Она имеет следующий исходный код.

Адресация модельных массивов графа
int relink(XPolyGraph *pg) {
vertex = pg->vertex; /* адрес массива вершин */
edge = pg->edge; /* адрес массива ребер */
face = pg->face; /* адрес массива граней */
return(0);
} /* relink */
После адресации модельных данных инициализируется статический массив palette, который кодирует доступ дисплейных функций к палитре цветов экрана. Его заполняет функция colorite, которую вызывает основная функция main для распределения цветов раскраски граней и контура графа. Ее аргумент адресует дисплейную структуру Display для идентификации палитры цветов экрана по умолчанию дисплейным макросом DefaultColormap. Набор цветов палитры задают символьные строки внутреннего массива spector спецификаций их RGB-компонент, которые записаны цифровыми парами системы счисления по основанию 16 в традиционном формате обозначения цветных X-ресурсов ("#RRGGBB"). Вместо цифрового кода, цвета могут быть заданы своими текстовыми именами из ресурсного файла (обычно, /usr/X11R6/lib/X11/rgb.txt) X Window System. При желании из него могут быть выбраны и специфицированы произвольные цифровые коды или имена цветов для распределения с учетом ограничений по экранной палитре.
Для распределения заданных цветов в палитру по умолчанию используются графические запросы XParseColor и XAllocColor последовательно для каждого цвета спектра. Они заполняют поля цветной структуры XColor для числовых значений RGB-компонент (red, green, blue) и пиксельного кода цвета (pixel).

Распределение палитры цветов
int colorite(Display* dpy) {
int scr; /* номер экрана (по умолчанию) */
Colormap cmap; /* палитра (карта) цветов экрана */
XColor rgb; /* цветная структура */
int i; /* спектральный номер цвета */
static char* spector[] = { /* Cпектр кодов (имен) цветов */
"#ffffff", /* или "W(w)hite" (белый) */
"#ff0000", /* или "R(r)ed" (красный) */
"#00ff00", /* или "G(g)reen" (зеленый) */
"#0000ff", /* или " B(b)lue" (синий) */
"#000000" /* или "B(b)lack" (черный) */
}; /* RGB-спецификация цветов */
scr = DefaultScreen(dpy); /* получить номер экрана (0) */
cmap = DefaultColormap(dpy, scr); /* экранная палитра */
for(i = 0; i < (NTONE+1); i++ ) { /* Спектральный цикл */
XParseColor(dpy, cmap, spector[i], &rgb); /* −> RGB */
XAllocColor(dpy, cmap, &rgb); /* −> pixel-код */
palette[i] = rgb.pixel; /* запомнить pixel-код цвета */
} /* for */
return(0);
} /* colorite */

Настройка графического контекста
Для цветного рисования графа дисплейные функции используют графический контекст, который формирует сервисная функция congraph. При этом за основу принимается графический контекст по умолчанию, который предоставляет дисплейный макрос DefaultGC для экрана по умолчанию. Его номер идентифицирует дисплейный макрос DefaultScreen. По запросу XChangeGC в структуре XGCValues параметров графического контекста переустанавливаются толщина линий для контура графа и цвет фона.
GC congraph(Display* dpy) {
int scr = DefaultScreen(dpy); /* номер экрана */
XGCValues gcval; /* параметры графконтекста */
GC gc; /* идентификатор графконтекста */
gcval.line_width = EWIDTH; /* толщина контура графа */
gcval.background = palette[DEFTONE]; /* код фона */
gc = DefaultGC(dpy, scr); /* Установка графконтекста */
XChangeGC(dpy, gc, GCLineWidth | GCBackground, &gcval);
return(gc); /* GC −> main */
} /* congraph */
Еще одна сервисная функция wingraph вызывается из основной функции main, чтобы создать окно изображения графа. Окно создается по графическому запросу XCreateWindow в центре экрана и сначала занимает 1/4 его площади. Такие начальные размеры и положение окна вычисляются с помощью дисплейных макросов DefaultWidth и DefaultHeight для номера экрана по умолчанию, который сообщает дисплейный макрос DefaultScreen. Окно программы также является подокном корневого окна экрана, которое идентифицирует дисплейный макрос DefaultRootWindow, наследуя его визуальный класс (CopyFromParent) с числом цветовых плоскостей по умолчанию, установленное дисплейным макросом DefaultDepth.

Создание и настройка параметров графического окна
Window wingraph(Display* dpy, char* title) {
Window root; /* идентификатор корневого окна экрана */
int scr; /* номер экрана по умолчанию */
int depth; /* число цветовых плоскостей экрана */
Window win; /* идентификатор окна программы */
XSetWindowAttributes attr; /* структура атрибутов окна */
XSizeHints hint; /* геометрия окнного менеджмента */
int x, y; /* координаты окна */
unsigned w, h; /* габариты окна */
unsigned long mask; /* маска атрибутов окна */
mask = CWOverrideRedirect | CWBackPixel | CWEventMask;
attr.override_redirect = False; /* WM-контроль окна */
attr.background_pixel = palette[DEFTONE]; /* цвет фона */
attr.event_mask = (ButtonPressMask | KeyPressMask |
ExposureMask | StructureNotifyMask |
FocusChangeMask); /* Маска событий */
root=DefaultRootWindow(dpy); /* корневое окно */
scr = DefaultScreen(dpy); /* номер экрана */
depth=DefaultDepth(dpy, scr); /* глубина экрана */
w = DisplayWidth(dpy, scr) / 2; /* Расположить окно */
h = DisplayHeight(dpy, scr) / 2; /* площадью 1/4 экрана */
x = w / 2; y = h / 2; /* в центре экрана */
win = XCreateWindow(dpy, root, x, y, w, h, 1, depth,
InputOutput, CopyFromParent, mask, &attr);
hint.flags = (PMinSize | PPosition | PMaxSize); /* Задать */
hint.min_width = hint.min_height = (8*VDOT); /* поля */
hint.max_width = 2*w; hint.max_height = 2*h; /* для */
hint.x = x; hint.y = y; /* геометрического свойства WM */
XSetNormalHints(dpy, win, &hint); /* −> свойство WM */
XStoreName(dpy, win, title); /* Задать заголовок окна */
XMapWindow(dpy, win); /* Отобразить окно на экране */
return(win); /* возврат идентификатока окна в main */
} /* wingraph */

Рисование графа в окне программы с помощью дисплейной функции regraph
Ее вызывает диспетчерская функция dispatch в цикле обработки событий после создания графического окна или потери изображения в нем. При вызове функции regraph передается адрес дисплейной структуры, идентификатор окна, графический контекст и флаг закраски граней NoFillFace. Если NoFillFace=0, производится раскраска граней в их цвета по запросам XSetForeground и XFillPolygon.
Исходный код рассмотренной функции regraph имеет следующий вид:
/* Перерисовка контура и перекраска граней графа */
int regraph(Display* dpy, Window win, GC gc, int NoFillFace) {
int i; /* счетчик вершин и граней */
/* Раскраска всех или 0 внутренних граней */
for(i = NoFillFace; i < NFACE; i++) {
XSetForeground(dpy, gc, palette[face[i].tone]); /* цвет грани */
XFillPolygon(dpy, win, gc, face[i].top, face[i].Cn,
Convex, CoordModeOrigin);
} /* for face */
/* Перерисовка всех ребер и вершин */
XSetForeground(dpy, gc, palette[NTONE]); /* −> Black */
XDrawSegments(dpy, win, gc, edge, NEDGE);
for(i = 0; i< NVERT; i++)
XFillArc(dpy, win, gc, vertex[i].x - (VDOT >> 1),
vertex[i].y - (VDOT >> 1),
VDOT, VDOT, 0, (64*360));
return(0);
} /* regraph */

Функция перерисовки граней
Для перерисовки отдельной грани после изменения ее цвета диспетчерская функция dispatch вызывает дисплейную функцию reface. При вызове ей передаются дисплейные параметры как в функцию regraph и номер грани для перерисовки (вместо флага закраски). Действие функции reface различается для внешней и внутренних граней графа. Перекраску внешней грани с номером NFACE обеспечивает вызов функции reset с аргументами функции reface. При этом происходит перезагрузка окна с перекраской его фона, который задает цвет внешней грани графа. Исходный текст функции reface имеет следующий вид.
/* Перекраска грани */
int reface(Display* dpy, Window win, GC gc, int f) {
int i; /* счетчик вершин грани */
if(f == NFACE) /* перекраска внешней грани */
return(reset(dpy, win, f));
XSetForeground(dpy, gc, palette[face[f].tone]);
XFillPolygon(dpy, win, gc, face[f].top, face[f].Cn,
Convex, CoordModeOrigin); /* Перекраска */
XFlush(dpy); /* внутренней грани */
/* Перерисовка контура грани */
XSetForeground(dpy, gc, palette[NTONE]); /* −> Black*/
XDrawLines(dpy, win, gc, face[f].top, face[f].Cn + 1,
CoordModeOrigin); /* перерисовка ребер */
for(i = 0; i< face[f].Cn; i++) /* перерисовка вершин */
XFillArc(dpy, win, gc, face[f].top[i].x − (VDOT/2),
face[f].top[i].y − (VDOT/2),
VDOT, VDOT, 0, (64*360));
return(0);
} /* reface */

Дисплейная функция reset
Дисплейная функция reset обеспечивает перезагрузку окна программы по клавиатурным сигналам в диспетчере событий dispatch или для перекраски внешней грани в функции reface. В любом случае ей передаются дисплейный адрес, идентификатор окна и параметр FillFace, который определяет результат перезагрузки. Если FillFace=0 (False), то фоновые индексы всех граней устанавливаются по цвету внешней грани для отмены раскраски. Когда FillFace=NFACE (True), они сохраняют свои значения, чтобы восстановить (освежить) раскраску всех внутренних граней. В обоих случаях запрос XSetWindowBackground переустанавливает фон графического окна в цвет внешней грани, который реализуется очисткой всей области окна по запросу XClearArea с нулевыми геометрическими параметрами. При этом значение True его последнего параметра генерирует событие типа Expose как при потере изображения в графическом окне программы. Функция reset выполняет больше действий, чем непосредственно специфицирует ее исходный код, который имеет следующий вид.
/* Перезагрузка раскраски граней */
int reset(Display* dpy, Window win, int FillFace) {
int f = FillFace; /* индекс грани */
/* Сохранить или Установить цвета внутренних граней */
for( ; f < NFACE; f++) /* по фону */
face[f].tone = face[NFACE].tone; /* внешней грани */
/* Установить фон окна и инициировать Expose */
XSetWindowBackground(dpy, win, palette[face[f].tone]);
XClearArea(dpy, win, 0, 0, 0, 0, True); /* −> Expose */
return(f);
} /* reset */