Содержание
- 2. Что нужно знать: рекурсия – это приём, позволяющий свести исходную задачу к одной или нескольким более
- 3. Сложив все значения, получим 25. 1 2 3 4 6 5 4
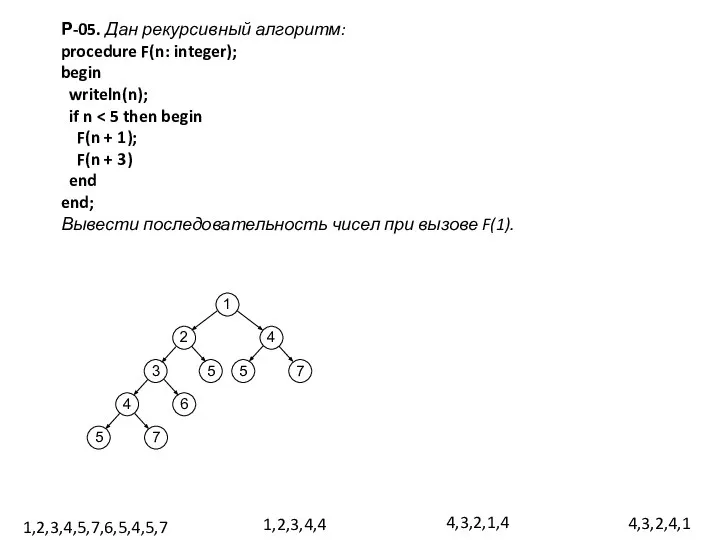
- 5. Р-05. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln(n); if n F(n + 1); F(n +
- 6. Р-03. Дан рекурсивный алгоритм: procedure F(n: integer); begin writeln('*'); if n > 0 then begin F(n-2);
- 8. Скачать презентацию




 Технология блокчейн в защите информации. Самостоятельная работа
Технология блокчейн в защите информации. Самостоятельная работа Представление вещественных чисел в двоичном коде (10 класс)
Представление вещественных чисел в двоичном коде (10 класс) Понятие об информационных системах и автоматизации информационных процессов
Понятие об информационных системах и автоматизации информационных процессов Современные математические подходы в моделировании
Современные математические подходы в моделировании Концепция электронного голосования
Концепция электронного голосования Веб-технология. Информатика для СПО
Веб-технология. Информатика для СПО Система управления базами данных моделирование и формализация. 9 класс
Система управления базами данных моделирование и формализация. 9 класс Структура проекта ASP.NET. Раздел № 1
Структура проекта ASP.NET. Раздел № 1 Дихотомический ключ
Дихотомический ключ Среда моделирования Rational Rose
Среда моделирования Rational Rose Компьютерная память
Компьютерная память Разработка автоматизированной информационной системы для ИТ-службы
Разработка автоматизированной информационной системы для ИТ-службы Сайт для голосований “Simple votings”
Сайт для голосований “Simple votings” Применение триггера в презентациях Power Point
Применение триггера в презентациях Power Point Сети. Устройство
Сети. Устройство Меняем характер чата
Меняем характер чата архив информации 6 лекция
архив информации 6 лекция Языки людей и языки программирования
Языки людей и языки программирования Логические основы работы компьютера
Логические основы работы компьютера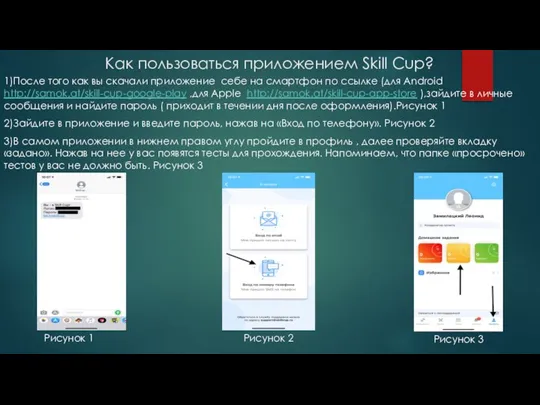 Как пользоваться приложением Skill Cup
Как пользоваться приложением Skill Cup Обработка графической информации
Обработка графической информации Переменные и их типы
Переменные и их типы Дигитайзеры
Дигитайзеры Я лисенок Вилли
Я лисенок Вилли Подключение к е-Факторинг 3.0
Подключение к е-Факторинг 3.0 Арифметичні і логічні основи цифрових і електронних обчислювальних машин
Арифметичні і логічні основи цифрових і електронних обчислювальних машин Қазіргі мәселелер және оларды шешу жолдары
Қазіргі мәселелер және оларды шешу жолдары Формы Бэкуса-Наура
Формы Бэкуса-Наура