Решение задач. Таблицы истинности. Комбинаторика. Делимость и конъюкция

№2 – таблицы истинности

Логическая функция F задаётся выражением ¬a ∨ (b ∧ ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы.

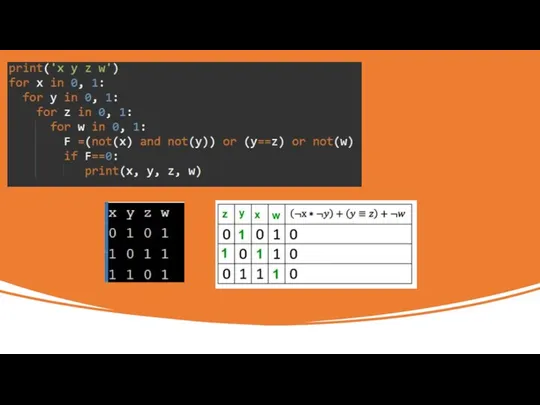
Миша заполнял таблицу истинности функции (¬x /\ ¬y) \/ (y ≡ z) \/ ¬w, но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных.
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Все три части функции связаны дизъюнкцией,
Следовательно, функция будет = 0 только тогда, когда каждая часть = 0

Логическая функция F задаётся выражением x ∨ (z ∧ ¬w) ∨ (y ∧ ¬w) ∨ (y ∧ ¬z). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F ложна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

САМОСТОЯТЕЛЬНО

Логическая функция F задаётся выражением x ∧ (y ∧ z ∨ z ∧ w ∨ y ∧ ¬w). На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

2. Логическая функция F задаётся выражением (x ∨ y) → (y ≡ z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.

Логическая функция F задаётся выражением (x ≡ ¬ y) → ((x ∧ w) ≡ z). На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z, w.

Ответы:
1- xzyw
2- yxz
3 - yzxw

№8 – комбинаторика

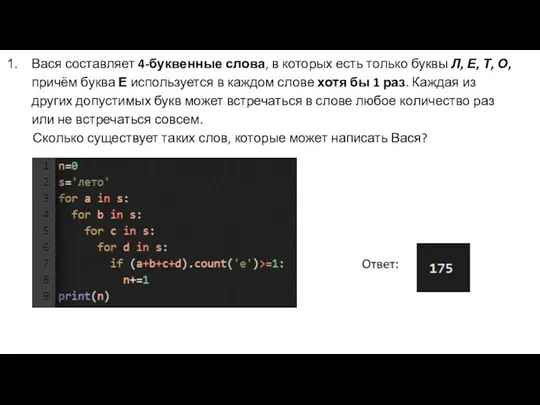
Вася составляет 4-буквенные слова, в которых есть только буквы Л, Е, Т, О, причём буква Е используется в каждом слове хотя бы 1 раз. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем.
Сколько существует таких слов, которые может написать Вася?

2. Олег составляет таблицу кодовых слов для передачи сообщений, каждому сообщению соответствует своё кодовое слово. В качестве кодовых слов Олег использует 4-буквенные слова, в которых есть только буквы A, Б, В, Г, Д и Е, причём буква Г появляется ровно 1 раз и только на первом или последнем месте. Каждая из других допустимых букв может встречаться в кодовом слове любое количество раз или не встречаться совсем. Сколько различных кодовых слов может использовать Олег?

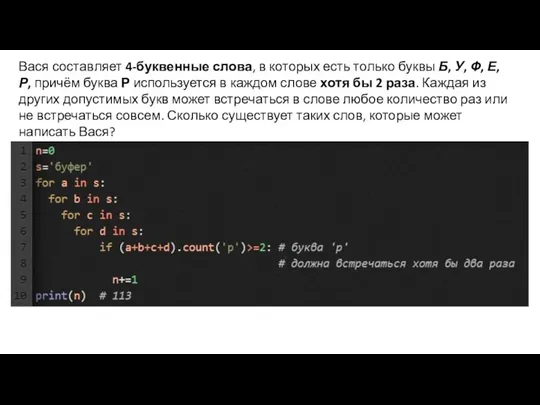
Вася составляет 4-буквенные слова, в которых есть только буквы Б, У, Ф, Е, Р, причём буква Р используется в каждом слове хотя бы 2 раза. Каждая из других допустимых букв может встречаться в слове любое количество раз или не встречаться совсем. Сколько существует таких слов, которые может написать Вася?

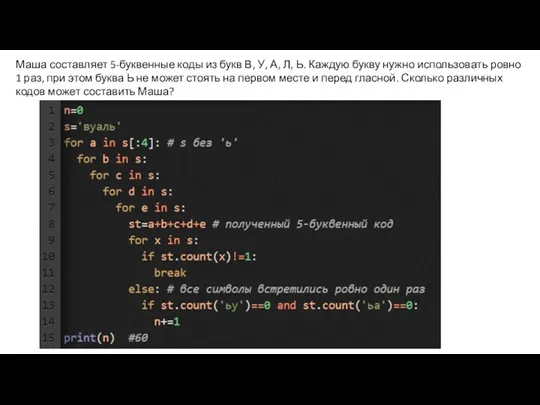
Маша составляет 5-буквенные коды из букв В, У, А, Л, Ь. Каждую букву нужно использовать ровно 1 раз, при этом буква Ь не может стоять на первом месте и перед гласной. Сколько различных кодов может составить Маша?

Самостоятельно
Сколь­ко четырёхбуквенных слов, на­чи­на­ю­щих­ся с со­глас­ной буквы и за­кан­чи­ва­ю­щихся глас­ной бук­вой, можно со­ста­вить из букв К, В, А, Н, Т? Каж­дая буква может вхо­дить в слово не­сколь­ко раз. Слова не обя­за­тель­но долж­ны быть осмыс­лен­ны­ми сло­ва­ми рус­ско­го языка.
Дима составляет 6-ти буквенные кодовые слова из букв А, К, Ц, Е, Н, Т.
Каждая буква встречается ровно один раз, причем буквы А и К, а также буквы Н и Т
должны стоять рядом. Сколько различных кодовых слов может составить Дима?
Дима составляет шестизначные числа, в которых есть только цифры 1,2 и 3, причём цифра 1 используется в каждом числе не более 2 раз и стоит на первом или на втором месте. Каждая из других допустимых цифр может встречаться в числе любое количество раз или не встречаться совсем. Числом считается любая допустимая последовательность цифр. Сколько существует таких чисел, которые может написать Дима?

Ответы
№1- 100
№2 – 96
№3 -144

№15 – делимость и конъюнкция

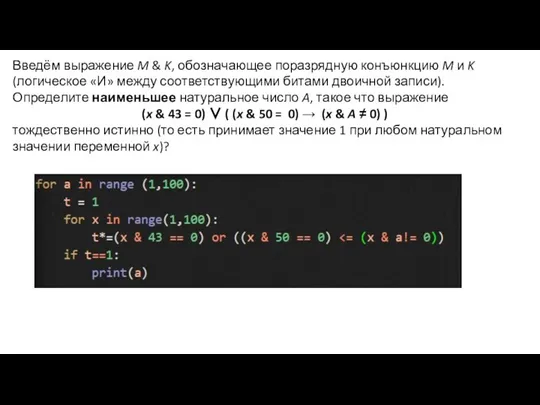
Введём выражение M & K, обозначающее поразрядную конъюнкцию M и K (логическое «И» между соответствующими битами двоичной записи).
Определите наименьшее натуральное число A, такое что выражение
(x & 43 = 0) ∨ ( (x & 50 = 0) → (x & A ≠ 0) )
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?

Определите наибольшее натуральное число A, такое что выражение
(x & A ≠ 0) → (((x & 17 = 0) ∧ (x & 5 = 0)) → (x & 3 ≠0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?

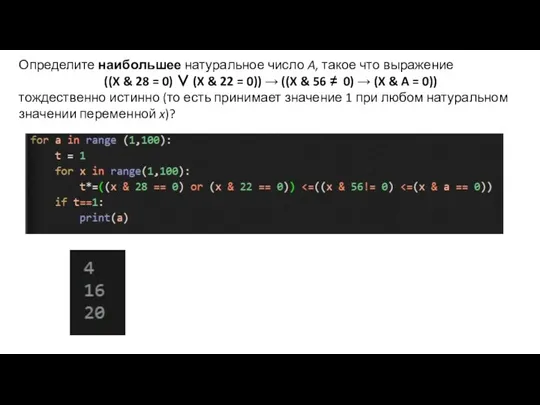
Определите наибольшее натуральное число A, такое что выражение
((X & 28 = 0) ∨ (X & 22 = 0)) → ((X & 56 ≠ 0) → (X & A = 0))
тождественно истинно (то есть принимает значение 1 при любом натуральном значении переменной x)?

Для какого наибольшего неотрицательного целого числа A формула
x&A≠0→((x&17=0⋀x&5=0)→x&3≠0)
тождественно истинна (т.е. принимает значение 1 при любом неотрицательном целом значении переменной x)?
Определите наибольшее натуральное число A, такое что выражение
(((X & 13 ≠ 0)∨(X & 39 = 0)) → (X & 13≠ 0)) ∨ ((X & A = 0) ∧ (X & 13 = 0))
тождественно истинно (то есть принимает значение 1
Для какого наименьшего неотрицательного целого числа A формула
(X & A = 0) ∧ ¬(X & 35 ≠ 0 → X & 52 ≠ 0)
тождественно ложна (то есть принимает значение 0)
Самостоятельно

Ответы.
№1-23
№2- 47
№3 - 3

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
ДЕЛ(x, А) → (ДЕЛ(x, 21) + ДЕЛ(x, 35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 21

Обозначим через ДЕЛ(n, m) утверждение «натуральное число n делится без остатка на натуральное число m». Для какого наименьшего натурального числа А формула
ДЕЛ(x, А) → (¬ДЕЛ(x, 21) + ДЕЛ(x, 35))
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 5

Самостоятельно
5. Для какого наибольшего натурального числа А формула
¬ДЕЛ(x,А)→(ДЕЛ(x,6)→ ¬ДЕЛ(x,9)) тождественно истинна?
6. Для какого наименьшего натурального числа А выражение
(ДЕЛ(x, А) ∧ ДЕЛ(x, 21)) → ДЕЛ(x, 18) тождественно истинно?
7. Для какого наибольшего натурального числа А формула
(¬ДЕЛ(x, А) ∧ ДЕЛ(x, 15)) → (¬ДЕЛ(x, 18) ∨ ¬ДЕЛ(x, 15)) тождественно истинна?
8. Для какого наименьшего натурального числа А формула
(ДЕЛ(x, А) ∧ ¬ДЕЛ(x, 15)) → (ДЕЛ(x, 18) ∨ ДЕЛ(x, 15)) тождественно истинна
9, Для какого наименьшего натурального числа А формула
(ДЕЛ(x, А) ∧ ДЕЛ(x, 12)) → (ДЕЛ(x, 42) ∨ ¬ДЕЛ(x, 12)) тождественно истинна?