Содержание
- 2. Понятие вычета по модулю Целые числа a и b сравнимы по модулю n (целому числу, неравному
- 3. Свойства вычетов -a {mod n} = -a+n {mod n} n=0 {mod n} Примеры: 3+10 {mod 12}
- 4. Свойства операций над вычетами аддитивности (a+b) {mod n} = (a {mod n} + b {mod n})
- 5. НОД и простые числа Наибольшим общим делителем (НОД) целых чисел a и b называется наибольшее целое
- 6. Функция Эйлера Если из полного набора вычетов по модулю n выделить подмножество вычетов, взаимно простых с
- 7. Функция Эйлера Очевидно, что если n является простым числом, то приведенный набор вычетов по модулю n
- 8. Китайская теорема об остатках (1-й век н.э.) Если m1, m2, …, mk – попарно взаимно простые
- 9. Пример использования теоремы об остатках Если x=1 {mod 2}, x=2 {mod 5} и x=3 {mod 9},
- 10. Малая теорема Ферма Если a – целое число, n – простое число и НОД(a, n)=1, то
- 11. Теорема Эйлера Является обобщением малой теоремы Ферма: если целые числа a и n являются взаимно простыми
- 12. Причины использования вычетов в криптографии Выполнение обратных операций (логарифмирование, извлечение корня, разложение на простые сомножители –
- 13. Способы симметричного шифрования Перестановки. Подстановки (замены). Гаммирование.
- 14. Шифры перестановок Биты (или символы) открытого текста переставляются в соответствии с задаваемым ключом шифрования правилом: ∀
- 15. Шифры перестановок При расшифровании применяется обратная перестановка: ∀ i, 1≤i≤n Pk[i]= Ci. Очевидно, что при шифровании
- 16. Шифры перестановок Пример. Пусть надо зашифровать слово «связной» (n=7) с помощью ключа k={4, 2, 1, 7,
- 17. Шифры перестановок Можно использовать и другой прием. После разбиения открытого текста длиной n на блоки, длина
- 18. Шифры перестановок При расшифровании шифротекст записывается в таблицу того же размера по строкам, затем происходит обратная
- 19. Шифры подстановок При шифровании с помощью подстановки (замены) каждый символ открытого текста заменяется другим символом одного
- 20. Одноалфавитная подстановка ∀ i, 1≤i≤n Ci=Pi+k {mod m}, где P= – открытый текст; n – длина
- 21. Одноалфавитная подстановка При расшифровании символ шифротекста заменяется символом, номер которого в используемом алфавите больше номера символа
- 22. Одноалфавитная подстановка К основным недостаткам относится: сохранение частоты появления различных символов открытого текста в шифротексте (одинаковые
- 23. Многоалфавитная подстановка ∀ i, 1≤i≤n Ci=Pi+ki {mod m}, где P= – открытый текст; n – длина
- 24. Многоалфавитная подстановка Расшифрование: ∀ i, 1≤i≤n Ci=Pi+m-ki {mod m}. Если длина ключа меньше длины открытого текста,
- 25. Многоалфавитная подстановка К достоинствам относится то, что в шифротексте маскируется частота появления различных символов открытого текста.
- 26. Шифры гаммирования Шифротекст получается путем наложения на открытый текст гаммы шифра с помощью какой-либо обратимой операции
- 27. Шифры гаммирования Расшифрование заключается в повторном наложении той же гаммы шифра на шифротекст: ∀ i, 1≤i≤n
- 28. Современные симметричные криптоалгоритмы Потоковые (результат шифрования каждого бита открытого текста зависит от ключа шифрования и значения
- 29. Потоковые шифры В основе лежит гаммирование. Криптостойкость полностью определяется структурой используемого генератора псевдослучайной последовательности (чем меньше
- 30. Потоковые шифры К наиболее известным относятся: RC4 (Rivest Cipher 4), разработанный Р.Ривестом (R.Rivest); в шифре RC4
- 31. Блочные шифры В этих криптосистемах открытый текст разбивается на блоки фиксированной, как правило, длины, и к
- 32. Блочные шифры К наиболее распространенным способам построения блочных шифров относится сеть Фейстела, при использовании которой каждый
- 34. Совершенный шифр ∀ X, Y p(X|Y)=p(X), где p(X) – вероятность выбора для шифрования открытого текста X,
- 35. Условия построения идеального (абсолютно стойкого) шифра Определены К.Шенноном: ключ шифрования вырабатывается совершенно случайным образом; один и
- 36. Условия К.Шеннона К сожалению, в большинстве случаев выполнение этих условий обеспечить практически невозможно, хотя короткие и
- 38. Скачать презентацию













![Шифры перестановок При расшифровании применяется обратная перестановка: ∀ i, 1≤i≤n Pk[i]= Ci.](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1004502/slide-14.jpg)

















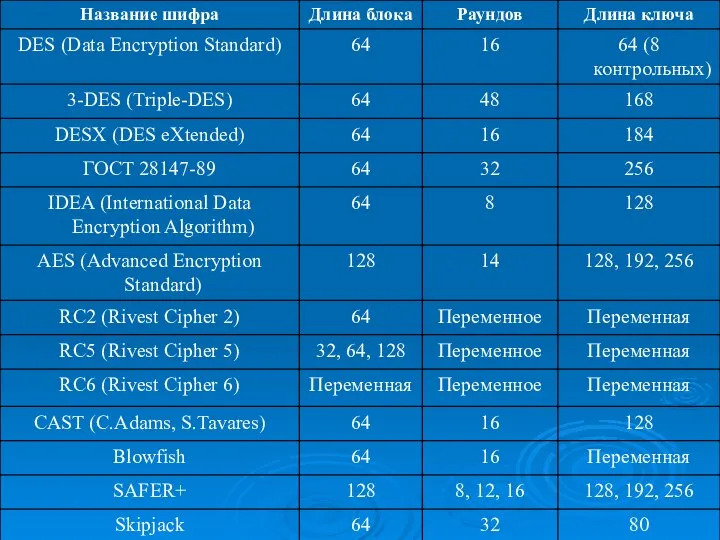



 Клуб Roy. Сервис совместного парамайнинга криптовалюты Prizm
Клуб Roy. Сервис совместного парамайнинга криптовалюты Prizm Регистрация в АИС ГТО
Регистрация в АИС ГТО Разработка мобильного приложения для поиска новых знакомств по интересам
Разработка мобильного приложения для поиска новых знакомств по интересам БСО: что это и как применяется
БСО: что это и как применяется Программные кассы
Программные кассы Выполнили: Слепцов Иван Игоревич Николаев Валерий Владимирович - 10 Б класса СОШ № 288. Научный руководитель:
Выполнили: Слепцов Иван Игоревич Николаев Валерий Владимирович - 10 Б класса СОШ № 288. Научный руководитель: Компьютеры и программы
Компьютеры и программы ЯП. Приложения с базами данных
ЯП. Приложения с базами данных Организация администрирования компьютерной системы Лечебный диагностический центр
Организация администрирования компьютерной системы Лечебный диагностический центр DH Standard AVN Update
DH Standard AVN Update Insribe Reader
Insribe Reader Создание компьютерной игры в среде Unity
Создание компьютерной игры в среде Unity Прямое и стилевое форматирование текста. Обработка текстовой информации
Прямое и стилевое форматирование текста. Обработка текстовой информации Зависимость грамотности блогеров от количества подписчиков и возраста блогера
Зависимость грамотности блогеров от количества подписчиков и возраста блогера Влияние СМИ на восприятие российскими гражданами работы органов государственной власти
Влияние СМИ на восприятие российскими гражданами работы органов государственной власти Абстрактные типы данных. Структуры данных
Абстрактные типы данных. Структуры данных Структуры и перечисления в С++. (Лекция 2)
Структуры и перечисления в С++. (Лекция 2) Информация и сигналы
Информация и сигналы Отчет о деятельности Пресс-центра ППОС СФУ за 2018 год
Отчет о деятельности Пресс-центра ППОС СФУ за 2018 год Дмнамическое формирование полей
Дмнамическое формирование полей Назначение программирования
Назначение программирования Регистры x86-64. Компьютерные основы программирования. Представление программ, часть 4
Регистры x86-64. Компьютерные основы программирования. Представление программ, часть 4 Занятие 1. Понятие об основных законах регулирования. Пропорциональный закон регулирования
Занятие 1. Понятие об основных законах регулирования. Пропорциональный закон регулирования Использование Linux при программировании 2
Использование Linux при программировании 2 Информационные технологии 2014-2020
Информационные технологии 2014-2020 Написание программы
Написание программы Сервис Datcom.kz, подписание документов электронной цифровой подписью
Сервис Datcom.kz, подписание документов электронной цифровой подписью Удаленное сопровождение клиентов. Сервисы 1С:ИТС для удаленной работы. Вебинар
Удаленное сопровождение клиентов. Сервисы 1С:ИТС для удаленной работы. Вебинар