Слайд 2Синтез нерекурсивных фильтров методом частотной выборки
В методе частотной выборки импульсная характеристика фильтра
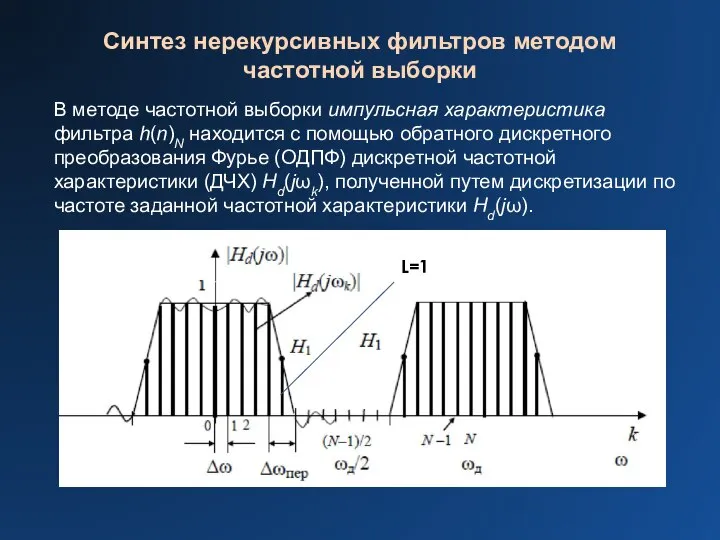
h(n)N находится с помощью обратного дискретного преобразования Фурье (ОДПФ) дискретной частотной характеристики (ДЧХ) Hd(jωk), полученной путем дискретизации по частоте заданной частотной характеристики Hd(jω).
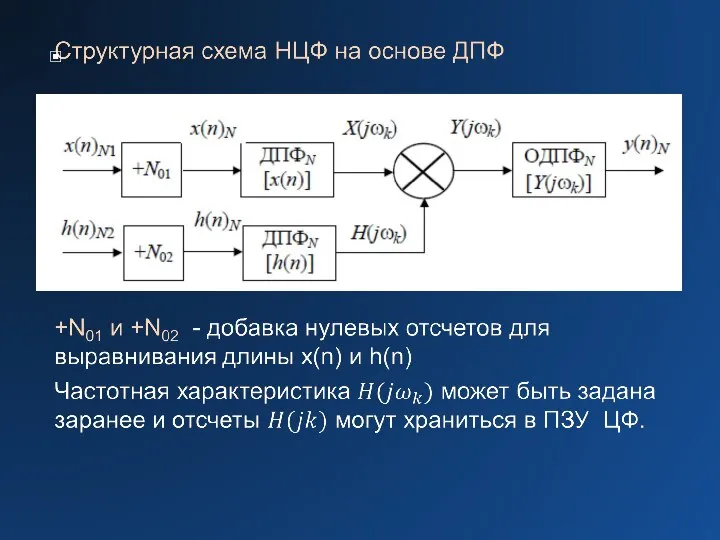
Слайд 6Алгоритм цифровой фильтрации сигналов
на основе дискретного преобразования Фурье

Слайд 10Алгоритм цифровой фильтрации
конечных последовательностей на основе ДПФ

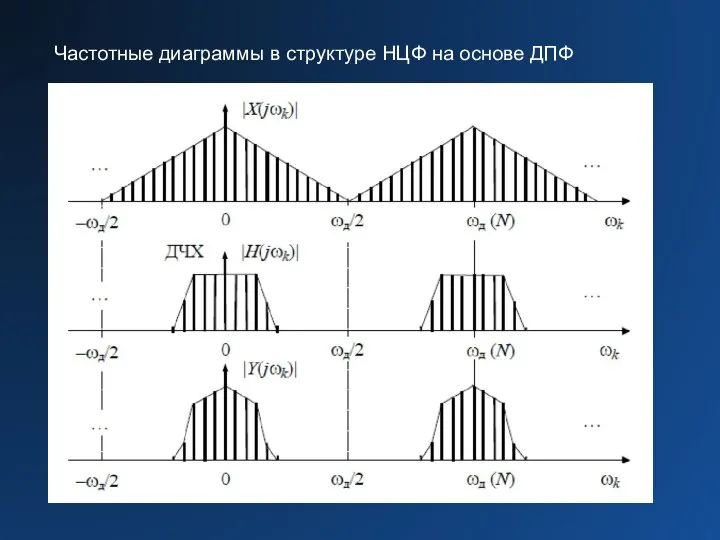
Слайд 12Частотные диаграммы в структуре НЦФ на основе ДПФ
Слайд 13Недостатки:
1. По объему вычислений фильтр на основе ДПФ уступает НФ на

основе ДВС, где на один отсчет сигнала выполняется N2 операции умножения.
Для рассматриваемого фильтра – число операций умножения Кумн = 4(2N2 +N) и сложения Ксл = 4(N -1)N, т.е. в пересчете на один отсчет:
Кумн(1) = 4(2N +1) и Ксл(1) = 4(N -1).
Однако при использовании быстрого преобразования Фурье (БПФ) ситуация меняется:
(пример: N =1024, НФ на основе БПФ - Кумн(1) = 44 и Ксл(1) = 40.
НФ на основе ДВС - Кумн(1) = Ксл(1) = 512).
2. Требуется значительный объем памяти.
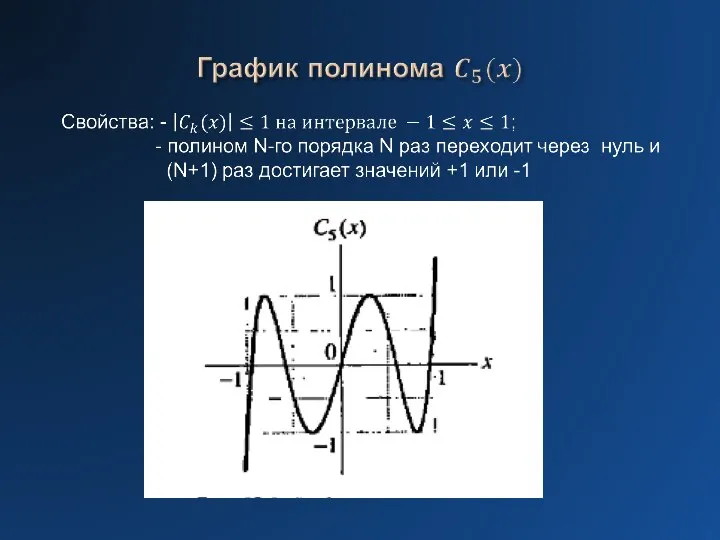
Слайд 15Численные методы синтеза цифровых фильтров

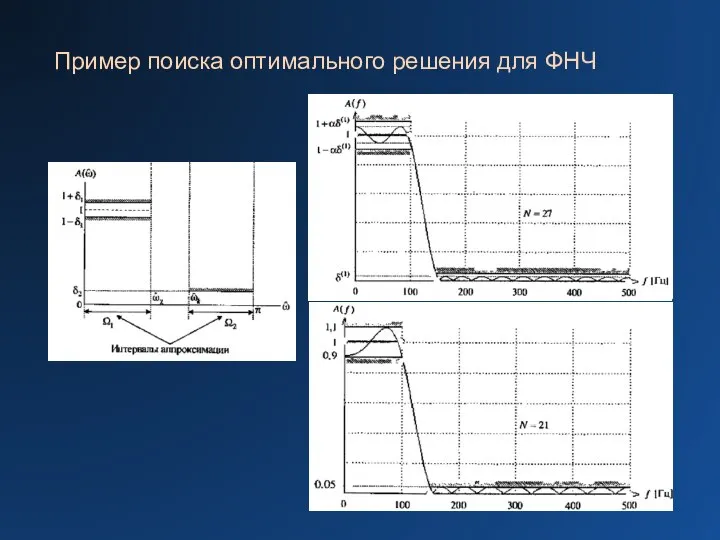
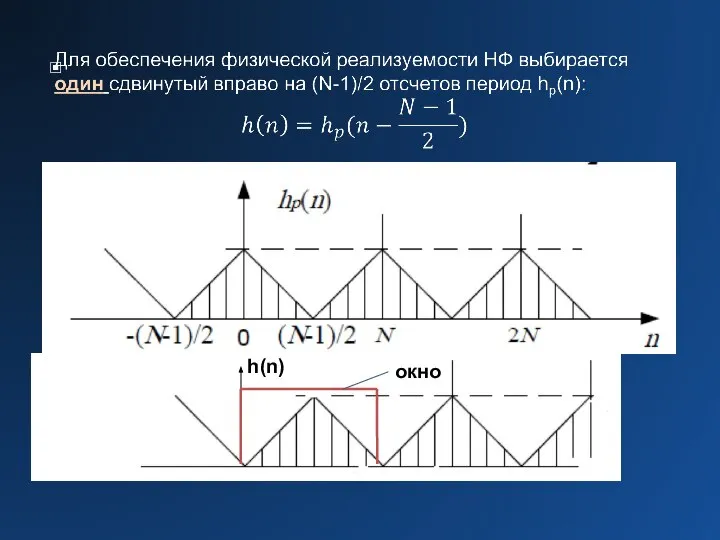
Слайд 18Пример поиска оптимального решения для ФНЧ
















 Способы представления графической информации Растровая и векторная графика
Способы представления графической информации Растровая и векторная графика Глобальные компьютерные сети
Глобальные компьютерные сети PHASE 1. Отладка
PHASE 1. Отладка SuperStar BTS для андроид
SuperStar BTS для андроид Создать форму для выбора блюд из меню с помощью приложения. Пример задания
Создать форму для выбора блюд из меню с помощью приложения. Пример задания IT-Practicum для тестировщиков
IT-Practicum для тестировщиков Техническое задание дизайнеру для HR
Техническое задание дизайнеру для HR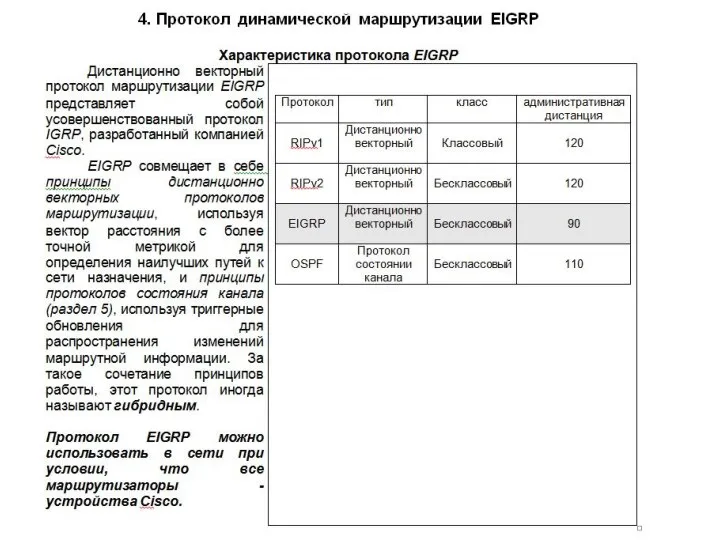 Протокол маршрутизации EIGRP
Протокол маршрутизации EIGRP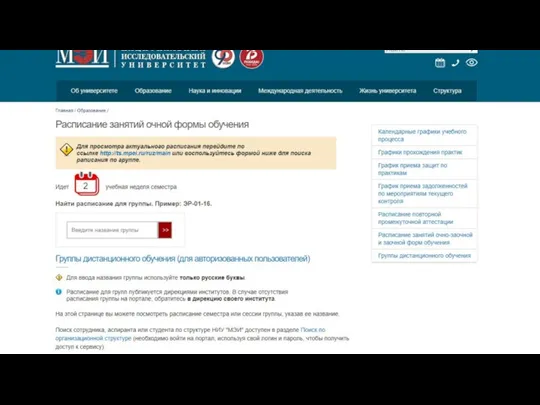 Расписание на сайте МЭИ
Расписание на сайте МЭИ Зарубежный опыт создания информационного общества и реализации электронного правительства (аналитический обзор)
Зарубежный опыт создания информационного общества и реализации электронного правительства (аналитический обзор) Python. Функции часть 1 (лекция 8)
Python. Функции часть 1 (лекция 8) Командная игра для 10-11 классов Виртуальный батл
Командная игра для 10-11 классов Виртуальный батл Современные возможности планшета в автомобиле
Современные возможности планшета в автомобиле Способы записи алгоритмов
Способы записи алгоритмов Введение в ГиперМетод
Введение в ГиперМетод Структуры
Структуры numPy
numPy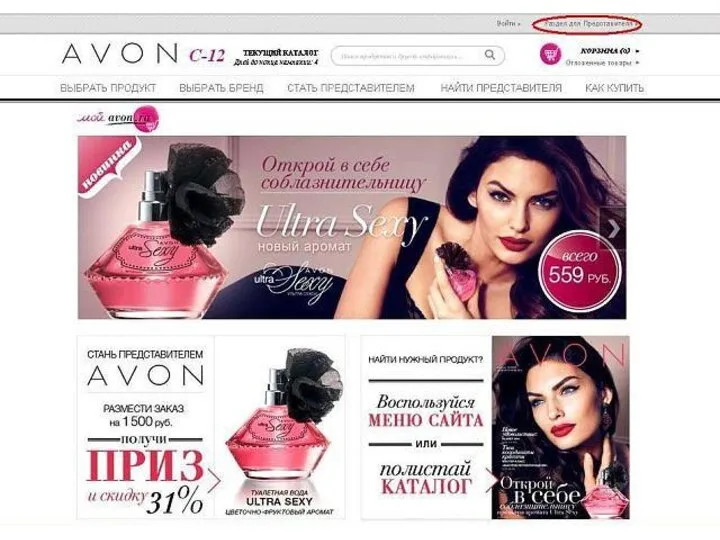 Как отправить заказ. Онлайн-магазин AVON
Как отправить заказ. Онлайн-магазин AVON Информационная система федерального института промышленной собственности РФ
Информационная система федерального института промышленной собственности РФ Разработка игры
Разработка игры (для учащихся 4-8 классов)
(для учащихся 4-8 классов) іт гр 32 урок 2
іт гр 32 урок 2 Sintez. Education center
Sintez. Education center Основные элементы системы управления базами данных Access
Основные элементы системы управления базами данных Access Инструкция для обучающихся КазНМУ по тестированию с прокторингом
Инструкция для обучающихся КазНМУ по тестированию с прокторингом Адресация в IP-сетях (2)
Адресация в IP-сетях (2) Правила оформления библиографического списка к Научной работе. Занятие 7
Правила оформления библиографического списка к Научной работе. Занятие 7 Интеллектуальные вычисления и сквозные цифровые технологии
Интеллектуальные вычисления и сквозные цифровые технологии