Системы счисления

Системы счисления (основные)
Двоичная: основание2, состоит из 2 знаков – 0 и 1.
Восьмиричная: основание 8, состоит из 8 знаков – 0,1,2,3,4,5,6,7
Десятичная: основание 10, состоит из 10 знаков – от0 до 9
Шестнадцатеричная: основание 16, состоит из цифр от 0 до 9 и букв лат.алф. От А до F

Правило перевода чисел из любой СС в десятичную:
Переводится число в 10 СС так:
1. Посчитать разряды числа справа налево от нуля:
6 5 4 3 2 1 0
11000112- основание системы счисления в которой дано число.
2. Записать число в развернутой форме:
Сносим разряд, умножаем на основание СС возведенное в степень порядкового номера разряда + следующий разряд …… :
11000112 = 1*26 + 1*25 +0*24 + 0*23 + 0*22 + 1*21 + 1*20 = =64+32+0+0+0+2+1 = 99
!Не забудь:
ЛЮБОЕ ЧИСЛО В НУЛЕВОЙ СТЕПЕНИ ДАЕТ 1
ЛЮБОЕ ЧИСЛО В ПЕРВОЙ СТЕПЕНИ – САМО ЧИСЛО

Правило перевода из десятичной СС в любую другую:
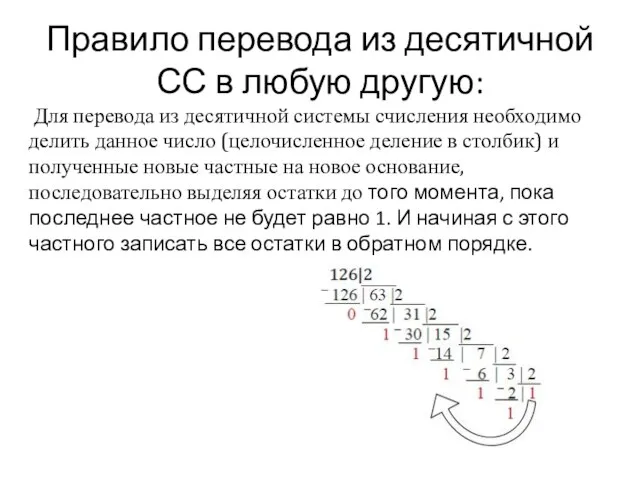
Для перевода из десятичной системы счисления необходимо делить данное число (целочисленное деление в столбик) и полученные новые частные на новое основание, последовательно выделяя остатки до того момента, пока последнее частное не будет равно 1. И начиная с этого частного записать все остатки в обратном порядке.

Альтернатива:
Можно использовать степени двойки
Использовать таблицу соответствия, но нельзя переводить через нее из десятичной и в десятичную

Правила степеней
Полезно помнить, что в двоичной системе:
четные числа оканчиваются на 0, нечетные – на 1;
числа, которые делятся на 2k, оканчиваются на k нулей,
например: 8 = 23 = 10002
числа вида 2k записываются в двоичной системе как единица и k нулей, например: 16 = 24 = 100002
числа вида 2k-1 записываются в двоичной системе k единиц, например: 15 = 24-1 = 11112
число 2N–2K при K < N в двоичной системе записывается как N–K единиц и K нулей
1+1=10 (так как нет цифры 2 в СС), 10-1=1

Выполнять перевод
Из 8СС и 16СС в 2СС
Из 2СС в 8СС и 16СС
Из 8СС в 16СС и наоборот, легче перевести через 2СС
Можно напрямую пользуясь таблицей соответствия, которую всегда можно составить, зная правила счета в различных системах счисления

Выполняя перевод напрямую помни:
Любой 8 знак соответствует 3 двоичным
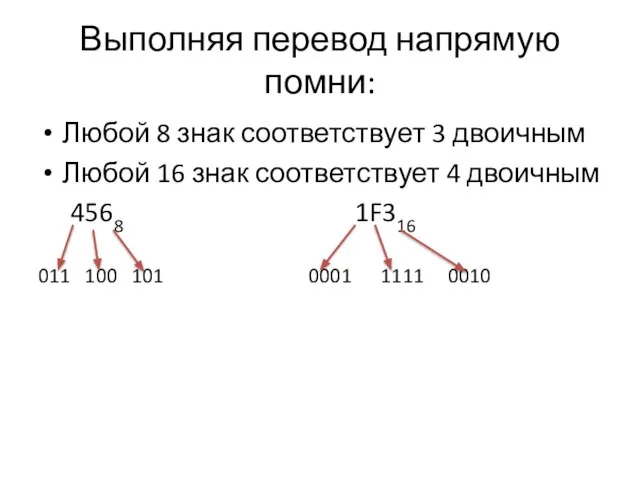
Любой 16 знак соответствует 4 двоичным
4568 1F316
011 100 101 0001 1111 0010

Отрицательное число:
Найти прямой код числа (перевести в 2 сс)
Добавить перед числом нули, если нет 8 знаков
Найти обратный код (меняем 1-0, 0-1)
Найти дополнительный код числа 9+1 в младший разряд)
-65=64+1=26 + 20 =1000001 (прямой)
01000001 (8 разрядный прямой код)
10111110 (обратный)
10111111 (дополнительный)
Единица в старшем разряде – знаковая, говорит о том, что число отрицательное

До 2019#13
Переведите число 259 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.
Переведите число 174 из десятичной системы счисления в двоичную систему счисления. Сколько нулей содержит полученное число? В ответе укажите одно число — количество нулей.
Переведите число -136 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.
Переведите число -93 из десятичной системы счисления в двоичную систему счисления. Сколько нулей содержит полученное число? В ответе укажите одно число — количество нулей.