Системы счисления

Системы счисления

Система счисления
это правила записи чисел с помощью специальных знаков – цифр, а также соответствующие правила выполнения операций с этими числами.
Числа: 123, 45678, 1010011, CXL
Цифры: 0, 1, 2, … I, V, X, L, …
Алфавит – это используемый в системе счисления набор цифр. {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}
Основание системы счисления – это количество цифр в алфавите (мощность алфавита).
Разряд – это позиция цифры в записи числа.

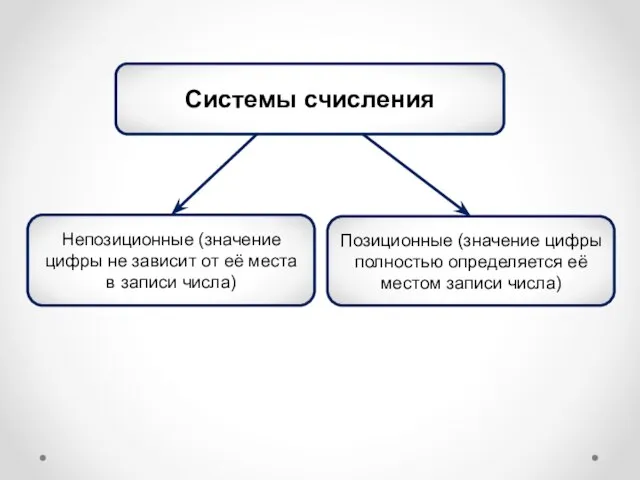
Системы счисления
Позиционные (значение цифры полностью определяется её местом записи числа)
Непозиционные (значение цифры не зависит от её места в записи числа)

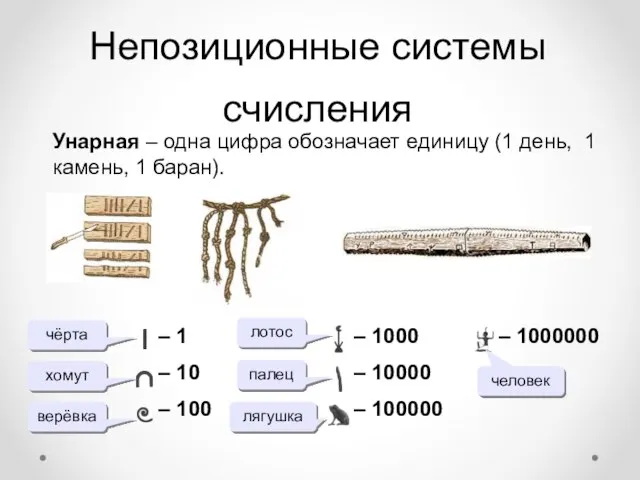
Непозиционные системы счисления
– 1
– 10
– 100
– 1000
– 10000
– 100000
– 1000000
чёрта
хомут
верёвка
лотос
палец
лягушка
человек
Унарная – одна цифра обозначает единицу (1 день, 1 камень, 1 баран).

Римская система счисления
В качестве цифр используются латинские буквы.
I – 1
V – 5
X – 10
L – 50
C – 100
D – 500
M - 1000

Правила
(обычно) не ставят больше трех
одинаковых цифр подряд;
если младшая цифра (только одна!) стоит слева от старшей, она вычитается из суммы (частично непозиционная!)

Римская система счисления
2389 = 2000 + 300 + 80 + 9
M M
CCC
LXXX
IX
Примеры:
MDCXLIV =
1000
+ 500
+ 100
– 10
+ 50
– 1
+ 5
= 1644

Недостатки римской системы счисления
возможность записывать только натуральные числа;
сложность в выполнении арифметических действий;
необходимость ввода новых цифр для записи больших чисел.

Где используется
Номера глав в книгах
Номера месяцев
Обозначение веков: «Пираты XX века»
Циферблат часов

Славянская система счисления

Славянская система счисления
алфавитная система счисления (непозиционная)

Позиционная система счисления
Десятичная система:
первоначально – счет на пальцах;
изобретена в Индии, заимствована арабами, завезена в Европу.
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10
3 7 8
2 1 0
разряды
8
70
300
= 3·102 + 7·101 + 8·100

Позиционная система счисления
Другие позиционные системы:
двоичная, восьмеричная, шестнадцатеричная (информатика);
двенадцатеричная (1 фут = 12 дюймов, 1 шиллинг = = 12 пенсов);
двадцатеричная (1 франк = 20 су);
шестидесятеричная (1 мин. = 60с, 1 ч. = 60 мин.).

Двоичная система счисления
Алфавит: 0, 1
Основание (количество цифр): 2
10 → 2
2 → 10
19
19 = 100112
система счисления
100112
4 3 2 1 0
разряды
= 1·24 + 0·23 + 0·22 + 1·21 + 1·20
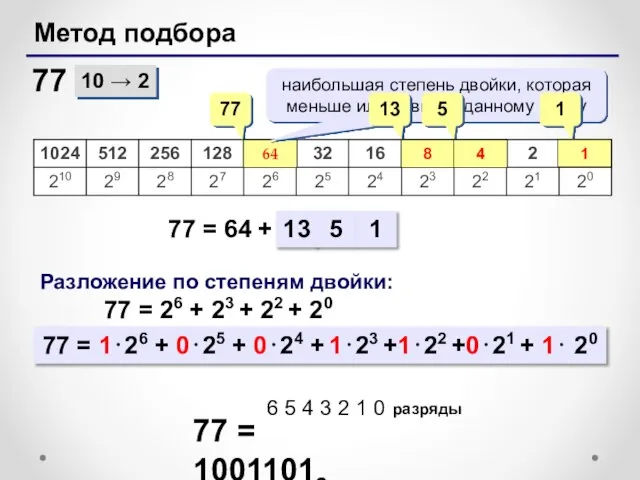
= 16 + 2 + 1 = 19

Метод подбора
10 → 2
77 = 64 +
77
77
64
Разложение по степеням двойки:
77 = 26 + 23 + 22 + 20
+ 8 + …
+ 4 + …
+ 1
77 = 10011012
6 5 4 3 2 1 0
разряды
наибольшая степень двойки, которая меньше или равна заданному числу
77 = 1⋅26 + 0⋅25 + 0⋅24 + 1⋅23 +1⋅22 +0⋅21 + 1⋅ 20
13
13
5
1
5
1
8
4
1

Восьмеричная система
Основание (количество цифр): 8
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7
10 → 8
8 → 10
101
101 = 1458
система счисления
1458
2 1 0
разряды
= 1·82 + 4·81 + 5·80
= 64 + 32 + 5 = 101

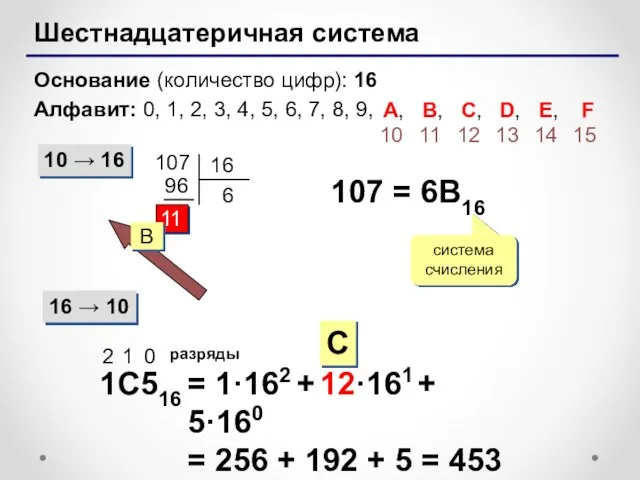
Шестнадцатеричная система
Основание (количество цифр): 16
Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,
10 → 16
16 → 10
107
107 = 6B16
система счисления
1C516
2 1 0
разряды
= 1·162 + 12·161 + 5·160
= 256 + 192 + 5 = 453
A,
10
B,
11
C,
12
D,
13
E,
14
F
15
B
C

Позиционные системы
Задача: в какой системе счисления число 58 записывается как «46x»? Определите основание системы счисления X.
в записи есть цифра 6, поэтому x > 6
переводим правую часть в десятичную систему
решаем уравнение
58 = 46x
1 0
58 = 46x
= 4·x1 + 6·x0
= 4·x + 6
58 = 4·x + 6
x = 13

Позиционные системы
Задача: найдите основание системы счисления, в которой выполняется равенство
в записи есть цифра 6, поэтому x > 6
переводим в десятичную систему
16x + 33x = 52x
x = 7
4·x + 9 = 5·x + 2
33x = 3·x + 3
1 0
решаем уравнение

Вопросы
Что такое система счисления?
Какие бывают системы счисления?
Что такое алфавит системы счисления? основание системы счисления?
Что такое разряд?
Как перевести число из любой позиционной системы счисления в десятичную?
Как перевести число из десятичной системы счисления в любую другую позиционную систему счисления?