л11 (1)

Учебные вопросы:
Системы счисления
Первые позиционные системы счисления
Современные позиционные системы
Перевод целых чисел из одной системы счисления в другую
Перевод дробных чисел из одной системы счисления в другую

1. Системы счисления
Для записи информации о количестве объектов используются числа. Числа записываются с помощью набора специальных символов.
Система счисления — способ записи чисел с помощью набора специальных знаков (алфавита), называемых цифрами.

В непозиционных системах счисления позиция, которую цифра занимает в записи числа, роли не играет.
В них вводится ряд символов для представления основных чисел, а остальные числа – результат их сложения и вычитания.
Например, римская система счисления.
Натуральные числа записываются при помощи повторения этих цифр (например, II – два, III – три, XXX – тридцать, CC – двести). Если же большая цифра стоит перед меньшей цифрой, то они складываются, если наоборот – вычитаются (например, VII – семь, IX – девять).
Непозиционные системы счисления
Основные символы в римской системе счисления

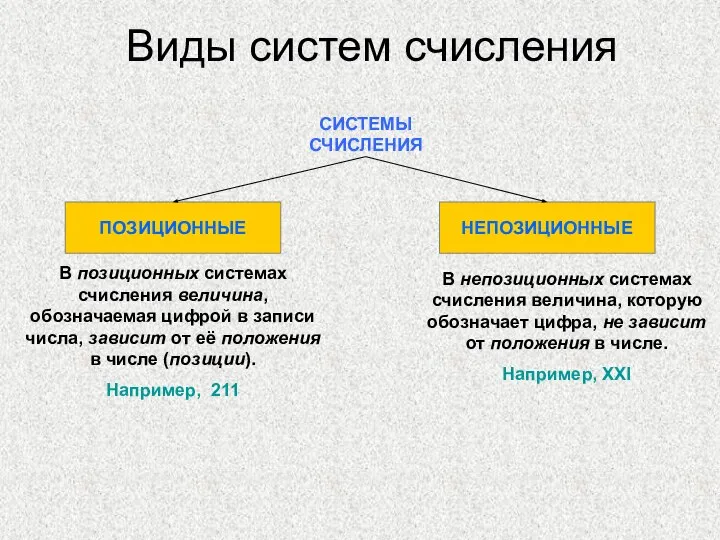
Виды систем счисления
СИСТЕМЫ СЧИСЛЕНИЯ
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
В непозиционных системах счисления величина, которую обозначает цифра, не зависит от положения в числе.
Например, XXI
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции).
Например, 211

Примеры
II = 1 + 1 = 2
Здесь символ I обозначает 1 независимо от места в числе.
Число 1988.
Одна тысяча M, девять сотен CM, восемьдесят LXXX, восемь VIII. Запишем их вместе: MCMLXXXVIII.
Проверка:
MCMLXXXVIII = 1000+(1000-100)+(50+10+10+10)+5+1+1+1 = 1988

Позиционные системы счисления
В позиционных системах счисления величина, обозначаемая цифрой в записи числа, зависит от её положения в числе (позиции).
Количество используемых цифр называется основанием системы счисления.
Например, 11 – это одиннадцать, а не два: 1 + 1 = 2 (сравните с римской системой счисления). Здесь символ 1 имеет различное значение в зависимости от позиции в числе.

2. Первые позиционные системы счисления
Самой первой такой системой, когда счетным "прибором" служили пальцы рук, была пятеричная.
Некоторые племена на филиппинских островах используют ее и в наши дни, а в цивилизованных странах ее реликт, как считают специалисты, сохранился только в виде пятибалльной шкалы оценок в образовательных учреждениях.

Двенадцатеричная система счисления
Следующей после пятеричной возникла двенадцатеричная система счисления.
Возникла она в древнем Шумере.
Некоторые учёные полагают, что такая система возникала у них из подсчёта фаланг на руке большим пальцем.
Широкое распространение получила двенадцатеричная система счисления в XIX веке.

На ее широкое использование в прошлом явно указывают названия числительных во многих языках, а также сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения:
Год состоит из 12 месяцев, а половина суток состоит из 12 часов.
Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия: 1 дюжина = 12 штук;
1 гросс = 12 дюжин = 144 штуки;
1 масса = 12 гроссов = 144 дюжины = 1728 штук.
Английский фунт до 1971 года состоял из 12 шиллингов.

Шестидесятеричная система счисления
Следующая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней использовалось шестьдесят цифр!
В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.

Позиционную систему счисления называют традиционной, если ее базис образует члены геометрической прогрессии, а значения цифр есть целые неотрицательные числа.
Базис-последовательность чисел каждая из которых задает вес соответствующего разряда.
Знаменатель P геометрической прогрессии, члены которой образуют базис традиционной системы счисления, называется основанием этой системы счисления.
Традиционные системы счисления с основанием P иначе называют P- ичным.

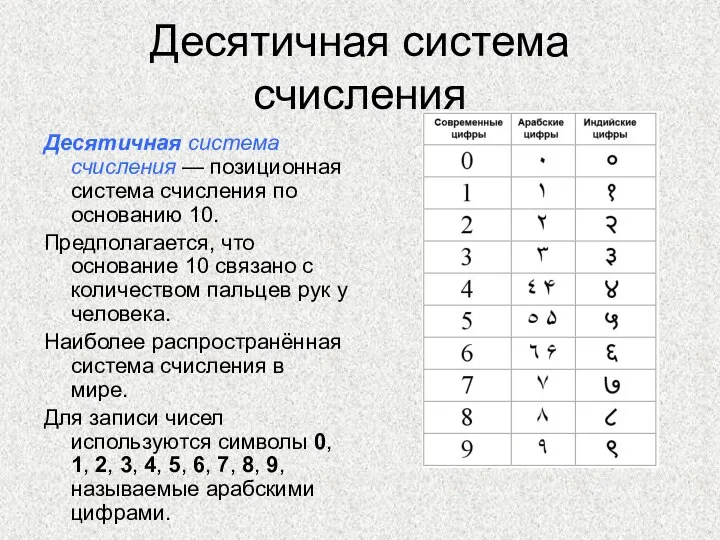
Десятичная система счисления
Десятичная система счисления — позиционная система счисления по основанию 10.
Предполагается, что основание 10 связано с количеством пальцев рук у человека.
Наиболее распространённая система счисления в мире.
Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.

3. Современные позиционные системы
В настоящее время наиболее распространены десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
Двоичная, восьмеричная (в настоящее время вытесняется шестнадцатеричной) и шестнадцатеричная система часто используется в областях, связанных с цифровыми устройствами, программировании и вообще компьютерной документации.
Современные компьютерные системы оперируют информацией представленной в цифровой форме. Числовые данные преобразуются в двоичную систему счисления.

Двоичная система счисления
Двоичная система счисления — позиционная система счисления с основанием 2. Используются цифры 0 и 1.
Двоичная система используется в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям:
Чем меньше значений существует в системе, тем проще изготовить отдельные элементы.
Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.
Простота создания таблиц сложения и умножения — основных действий над числами.

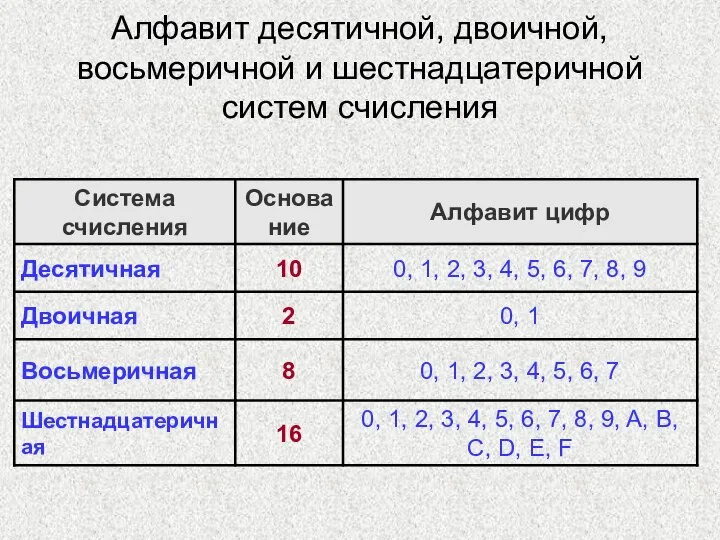
Алфавит десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления

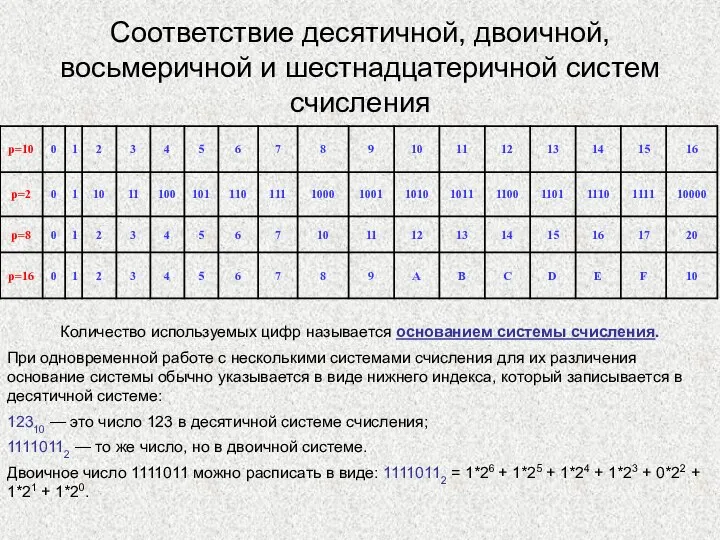
Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
Количество используемых цифр называется основанием системы счисления.
При одновременной работе с несколькими системами счисления для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:
12310 — это число 123 в десятичной системе счисления;
11110112 — то же число, но в двоичной системе.
Двоичное число 1111011 можно расписать в виде: 11110112 = 1*26 + 1*25 + 1*24 + 1*23 + 0*22 + 1*21 + 1*20.

где А-само число, P-основание системы счисления, а-цифры данной системы счисления, n-число разрядов целой части числа, m-число разрядов дробной части числа.
Пример:
Развернутая форма записи числа
единицы
десятки
сотни
тысячи

4. Перевод целых чисел из одной системы счисления в другую
Чтобы перевести целое число из позиционной системы счисления с основанием p в десятичную, надо представить это число в виде суммы степеней p и произвести указанные вычисления в десятичной системе счисления.
Например, переведем число 10112 в десятичную систему счисления. Для этого представим это число в виде степеней двойки и произведем вычисления в десятичной системе счисления.
10112 = 1*23 + 0*22 + 1*21 + 1*20 = 1*8 + 0*4 + 1*2 + 1*1 = 8 + 0 + 2 + 1 = 1110
Рассмотрим пример. Переведем число 52,748 в десятичную систему счисления.
52,748 = 5*81 + 2*80 + 7*8-1 + 4*8-2 = 5*8 + 2*1 + 7*1/8 +4*1/49 = 40 + 2 + 0,875 + 0,0625 = 42,937510

Переведем десятичное число 2010 в двоичную систем счисления (основание системы счисления p=2).
В итоге получили 2010 = 101002.
Перевод целых чисел из десятичной системы счисления в систему счисления с основанием p осуществляется последовательным делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.

315
24
75
72
3
8
32
7
8
4
315
16
9
16
155
144
11
(В)
16
3
16
1
13
2
2
2
12
1
6
6
0
3
2
1
1
Перевод целых чисел из десятичной в другие
системы счисления
Двоичная 1310=X2
Восьмеричная 31510=Y8
Шестнадцатеричная 31510=Z16
3
1
9

5. Перевод дробных чисел из одной системы счисления в другую
Правило перевода дробных чисел из одной системы счисления в другую:
последовательно умножать данное число и получаемые дробные части произведений на основание новой системы, выраженное цифрами исходной системы, до тех пор, пока дробная часть произведения не станет равной нулю или не будет достигнута требуемая точность;

2) полученные целые части произведений, являющиеся цифрами числа в новой системе, выразить цифрами алфавита этой системы;

3) составить дробную часть числа в новой системе, начиная с целой части первого произведения.

Переводы в смешанных системах
Из 2-ной системы в 8-ную (двоично-восьмеричное
изображение):
из 8-ной системы в 2–ную (восьмерично-двоичное
изображение):

Переводы в смешанных системах
из 2-ной системы в 16-ную (двоично-шестнадцатеричное
изображение):
из 16-ной системы в 2-ную (шестнадцатерично-двоичное
изображение):

Вопросы:
Что такое система счисления?
Какие два вида систем счисления вы знаете?
Что такое основание системы счисления? Что такое алфавит системы счисления? Примеры.
В какой системе счисления хранятся и обрабатываются числа в памяти компьютера?