Содержание
- 2. Что такое система счисления? Система счисления — это правила записи чисел с помощью специальных знаков —
- 3. Египетская десятичная система – 1 – 10 – 100 – 1000 – 10000 – 100000 –
- 4. Прислать на почту [email protected] ответы: Записать в египетской системе счисления числа: 1. 5371 2. 1111 3.
- 5. Непозиционные системы счисления Непозиционная система счисления: значение цифры не зависит от её места в записи числа.
- 6. Римская непозиционная СС (500 лет до н.э.) Используется обозначение веков, номера глав в книгах, циферблат часов
- 7. Римская система счисления I – 1 (палец), V – 5 (раскрытая ладонь, 5 пальцев), X –
- 8. Римская система счисления Правила: (обычно) не ставят больше трех одинаковых цифр подряд если младшая цифра (только
- 9. Римская непозиционная СС если меньшая цифра стоит слева от большей IX (10-1=9) если меньшие цифры стоят
- 10. Римская система счисления MCDLXVII = MMDCXLIV = MMMCCLXXII = CMXXVIII = Прислать на почту [email protected] ответы:
- 11. Римская система счисления 3768 = 2983 = 1452 = 1999 = Прислать на почту [email protected] ответы:
- 12. Римская система счисления только натуральные числа (дробные? отрицательные?) для записи больших чисел нужно вводить новые цифры
- 13. Славянская система счисления алфавитная система счисления (непозиционная) Часы Суздальского Кремля
- 14. Славянская система счисления = 800+60+3 = 863 Использовалась она нечасто, но достаточно долго. По организации повторяет
- 15. Славянская система счисления Славянская кириллическая десятеричная алфавитная
- 16. Запишите в славянской системе счисления числа и пришлите на почтуПрислать на почту [email protected] ответы: 10321 1948
- 17. Системы счисления § 10. Позиционные системы счисления
- 18. Определения Позиционная система: значение цифры определяется ее позицией в записи числа. Алфавит системы счисления — это
- 19. Формы записи чисел 6 3 7 5 3 2 1 0 разряды 5 70 300 =
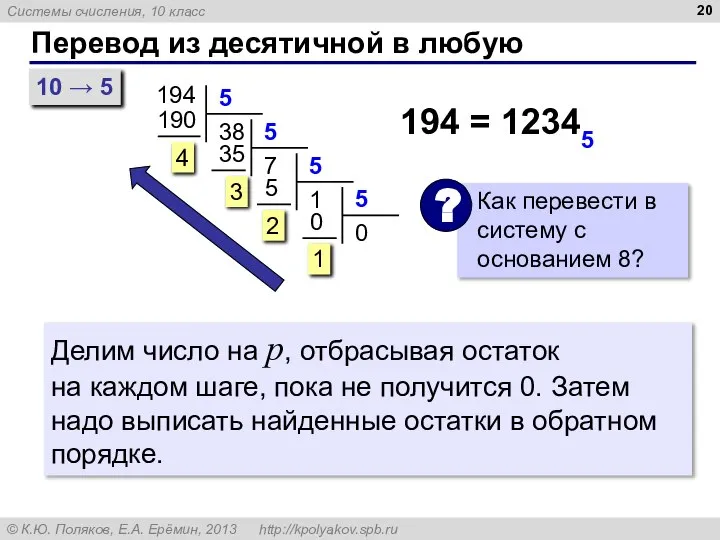
- 20. Перевод из десятичной в любую 194 194 = 12345 10 → 5 Делим число на p,
- 21. Перевести в двоичную систему счисления числа 4= 5= 6= 7= 8= 9= 10= 11= 12= 13=
- 22. в записи есть цифра 6, поэтому X > 6 переводим правую часть в десятичную систему решаем
- 23. в записи есть цифра 5, поэтому X > 5 переводим правую часть в десятичную систему решаем
- 24. Задачи Задача: найдите все основания систем счисления, в которых запись десятичного числа 24 оканчивается на 3.
- 25. Задачи Задача: найдите все десятичные числа, не превосходящие 40, запись которых в системе счисления с основанием
- 26. Задачи Задача: Все 5-буквенные слова, составленные из букв А, О и У, записаны в алфавитном порядке.
- 27. Дробные числа 0,6375 = 6·0,1 + 3·0,01 + 7·0,001 + 5·0,0001 0, 6 3 7 5
- 28. Дробные числа: из десятичной в любую 0,12345 = 5-1·(1 + 5-1·(2 + 5-1·(3 + 5-1·4))) 5·(0,12345)=
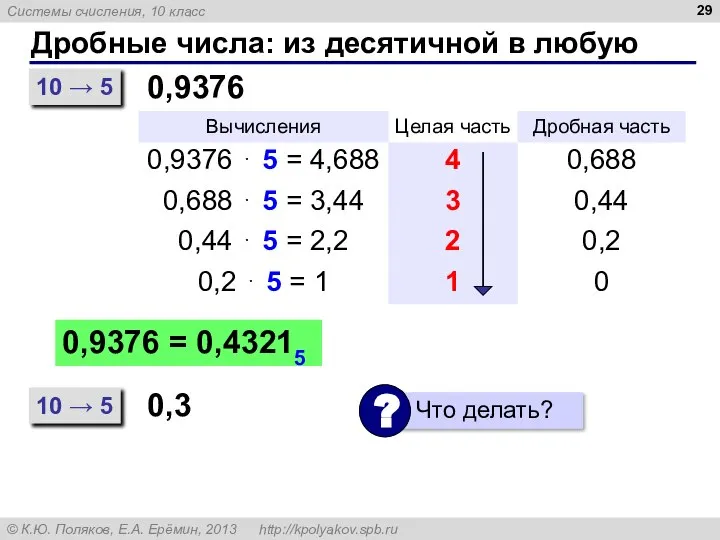
- 29. Дробные числа: из десятичной в любую 10 → 5 0,9376 0,9376 = 0,43215 10 → 5
- 30. Дробные числа: из десятичной в любую 10 → 6 25,375 = 25 + 0,375
- 31. Системы счисления § 11. Двоичная система счисления
- 32. Двоичная система Основание (количество цифр): 2 Алфавит: 0, 1 10 → 2 2 → 10 19
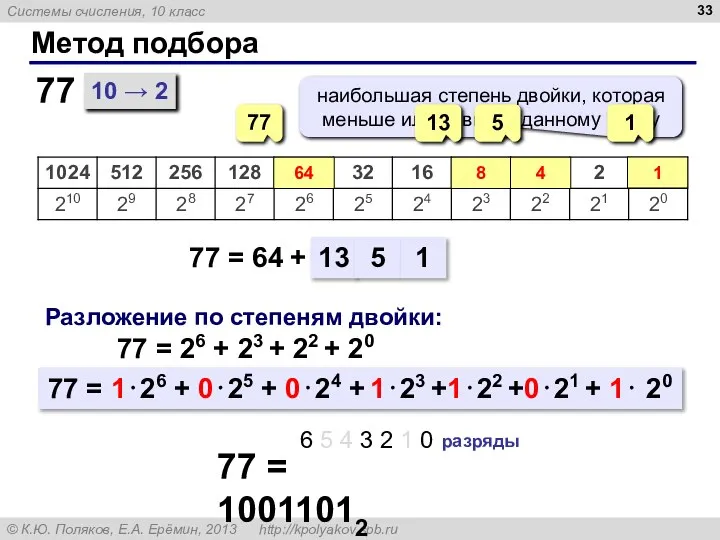
- 33. Метод подбора 10 → 2 77 = 64 + 77 77 64 Разложение по степеням двойки:
- 34. Перевод из двоичной в десятичную 10011012 = 26 + 23 + 22 + 20 6 5
- 35. Арифметические операции сложение вычитание 0+0=0 0+1=1 1+0=1 1+1=102 1 + 1 + 1 = 112 0-0=0
- 36. Арифметические операции
- 37. Арифметические операции
- 38. Арифметические операции умножение деление 1 0 1 0 12 × 1 0 12 1 0 1
- 39. Дробные числа 10 → 2 0,8125 0,8125 = 0,11012 10 → 2 0,6 = 0,100110011001… =
- 40. Дробные числа Большинство дробных чисел хранится в памяти с некоторой погрешностью. При выполнении вычислений с дробными
- 41. Двоичная система счисления длинная запись чисел: 1024 = 100000000002 запись однородна (только 0 и 1) нужны
- 42. Системы счисления § 12. Восьмеричная система счисления
- 43. Восьмеричная система счисления Основание: 8 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7 10 →
- 44. Примеры 134 = 75 = 1348 = 758 =
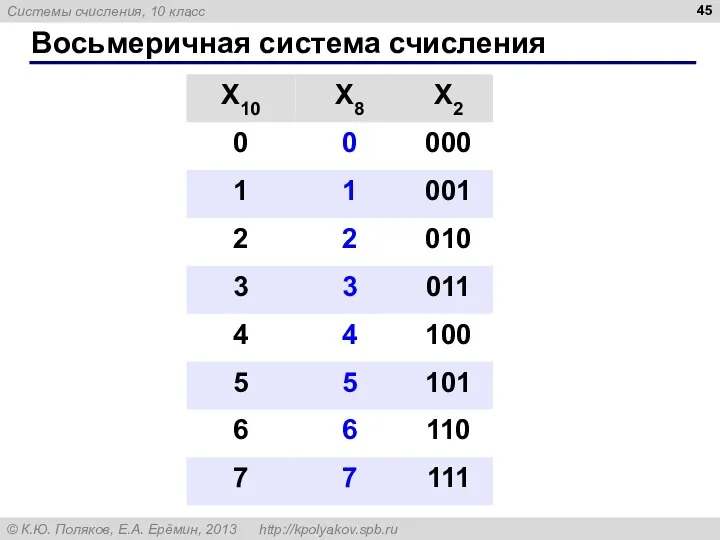
- 45. Восьмеричная система счисления
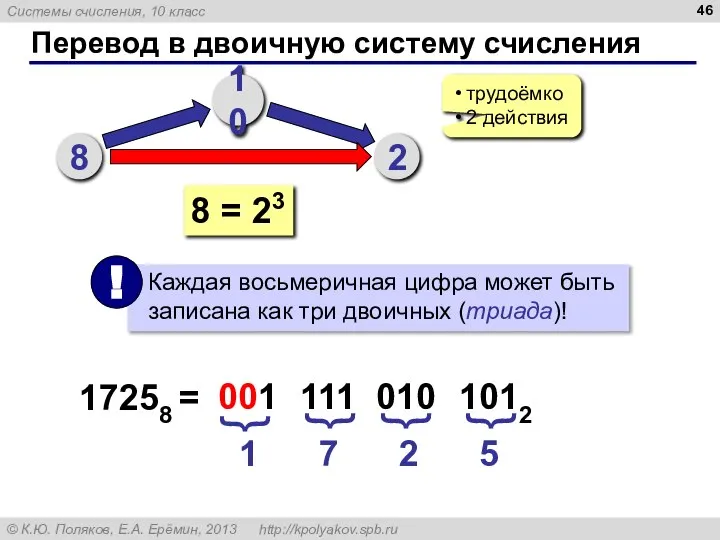
- 46. Перевод в двоичную систему счисления 8 10 2 трудоёмко 2 действия 8 = 23 17258 =
- 47. Примеры 34678 = 21488 = 73528 = 12318 =
- 48. Перевод из двоичной в восьмеричную 10010111011112 Шаг 1. Разбить на триады, начиная справа: 001 001 011
- 49. Примеры 1011010100102 = 111111010112 = 11010110102 =
- 50. Арифметические операции сложение 1 5 68 + 6 6 28 1 1 6 + 2 =
- 51. Примеры
- 52. Арифметические операции вычитание 4 5 68 – 2 7 78 ∙ (6 + 8) – 7
- 53. Примеры
- 54. Системы счисления § 13. Шестнадцатеричная система счисления
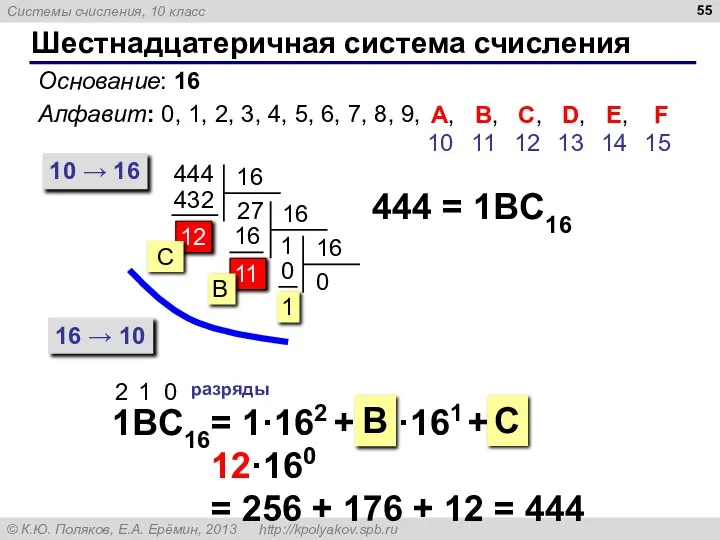
- 55. 11 Шестнадцатеричная система счисления Основание: 16 Алфавит: 0, 1, 2, 3, 4, 5, 6, 7, 8,
- 56. Примеры 171 = 206 = 1C516 = 22B16 =
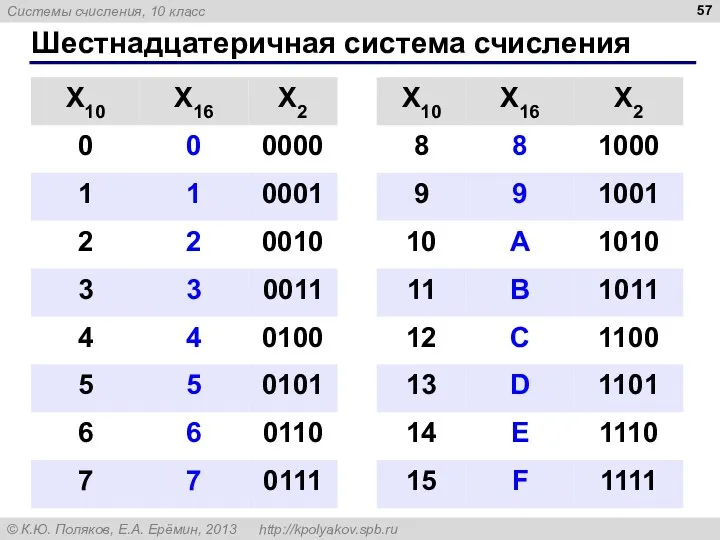
- 57. Шестнадцатеричная система счисления
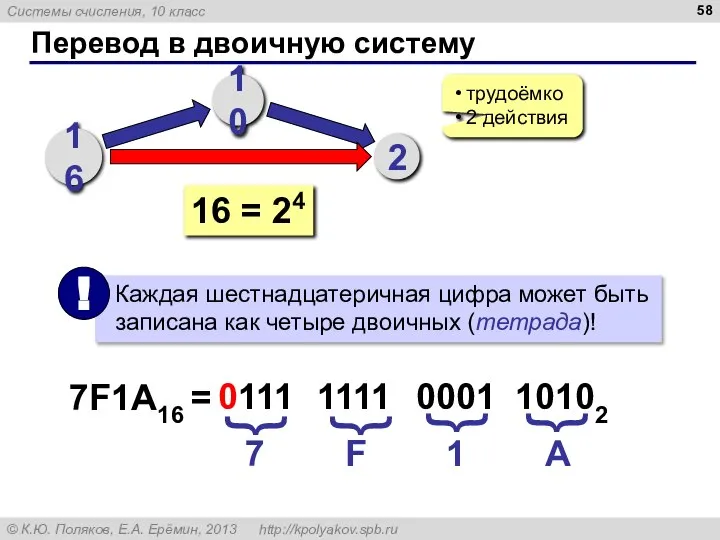
- 58. Перевод в двоичную систему 16 10 2 трудоёмко 2 действия 16 = 24 7F1A16 = 7
- 59. Примеры C73B16 = 2FE116 =
- 60. Перевод из двоичной системы Шаг 1. Разбить на тетрады, начиная справа: 0001 0010 1110 11112 Шаг
- 61. Примеры 10101011010101102 = 1111001101111101012 = 1101101101011111102 =
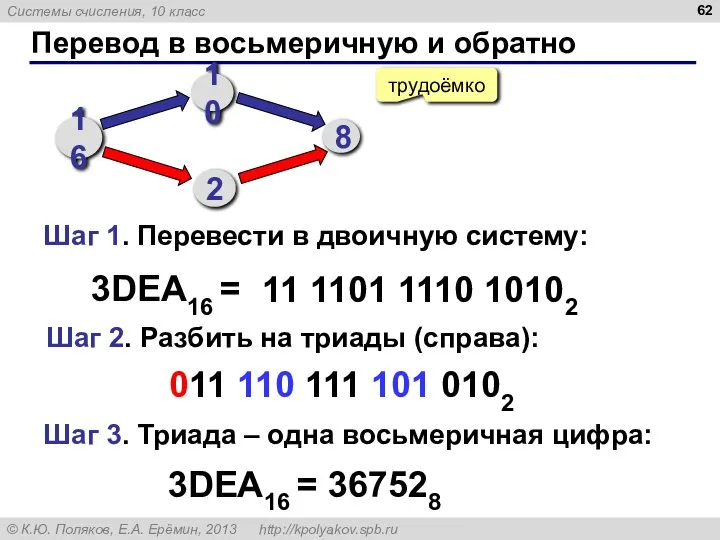
- 62. Перевод в восьмеричную и обратно трудоёмко 3DEA16 = 11 1101 1110 10102 16 10 8 2
- 63. Примеры A3516 = 7658 =
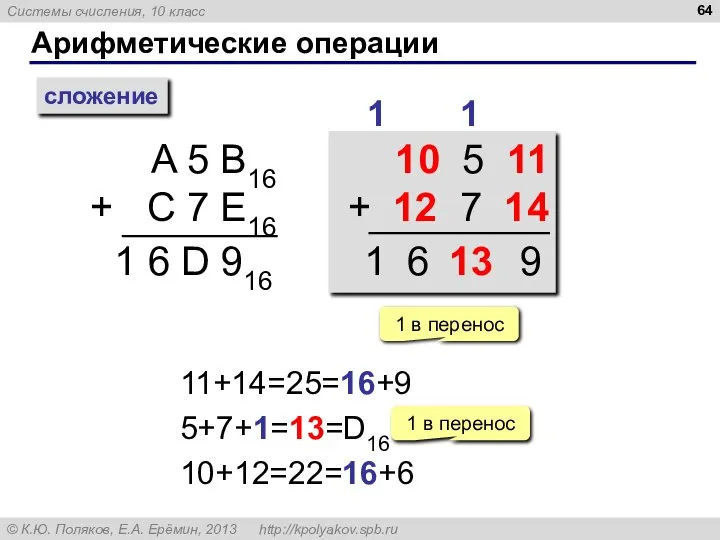
- 64. Арифметические операции сложение A 5 B16 + C 7 E16 1 1 6 D 916 10
- 65. Примеры С В А16 + A 5 916 F D В16 + A B C16
- 66. Арифметические операции вычитание С 5 B16 – A 7 E16 заём ∙ 1 D D16 12
- 67. Примеры 1 В А16 – A 5 916
- 68. Системы счисления § 14. Другие системы счисления
- 69. Задача Баше о наборе гирь + 1 гиря на правой чашке 0 гиря снята – 1
- 70. Троичная уравновешенная система ЭВМ «Сетунь» (1958) , Н.П. Брусенцов Основание: 3 Алфавит: («-1»), 0, 1 Для
- 71. Двоично-десятичная система (ДДС) Десятичные цифры, закодированные в двоичном коде. Вinary coded decimal (BCD). 9024,19 = 1001
- 72. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург [email protected] ЕРЕМИН
- 74. Скачать презентацию



























































 Разработка программного обеспечения автоматизираванного рабочего места специалиста отдела продаж ОАО Лидские Пищевые Концетраты
Разработка программного обеспечения автоматизираванного рабочего места специалиста отдела продаж ОАО Лидские Пищевые Концетраты Баги и баг-трекеры
Баги и баг-трекеры Поразрядные операторы
Поразрядные операторы Ежегодные мероприятия университета Частного права
Ежегодные мероприятия университета Частного права Массивы
Массивы Компьютерные сети
Компьютерные сети Центр автоматизации энергосбережения
Центр автоматизации энергосбережения servis
servis Kibersport_2
Kibersport_2 Аналитическая бизнес-справка на ЮЛ
Аналитическая бизнес-справка на ЮЛ Безопасный Интернет
Безопасный Интернет Организация вычислений в электронных таблицах. Обработка числовой информации в электронных таблицах
Организация вычислений в электронных таблицах. Обработка числовой информации в электронных таблицах Обработка массивов
Обработка массивов Поняття бази даних
Поняття бази даних Фрактальная графика - fractus
Фрактальная графика - fractus Направления развития информатики
Направления развития информатики Общение в Интернете
Общение в Интернете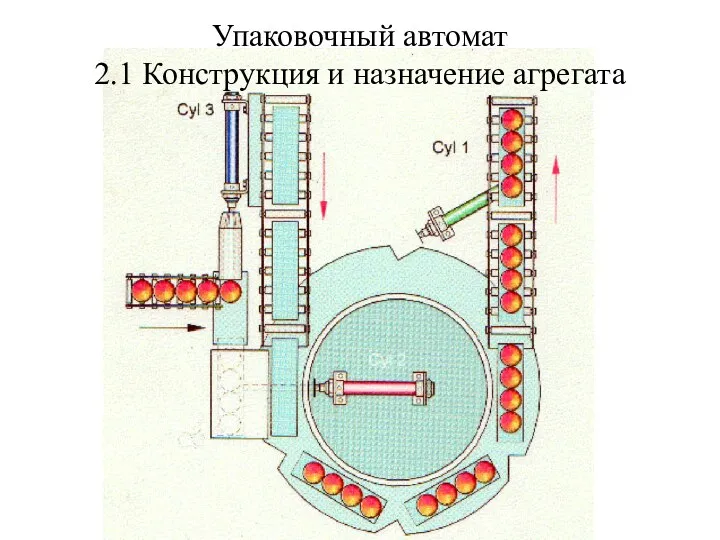 Упаковочный автомат. Конструкция и назначение агрегата
Упаковочный автомат. Конструкция и назначение агрегата Виды источников информации
Виды источников информации Оптимизатор Solver (встроен в Microsoft Excel)
Оптимизатор Solver (встроен в Microsoft Excel) Основы баз данных
Основы баз данных Практикум: Составление блок-схем алгоритмов линейной структуры
Практикум: Составление блок-схем алгоритмов линейной структуры Агрегирование с использованием групповых функций
Агрегирование с использованием групповых функций Дашборд - общая информация статистика
Дашборд - общая информация статистика Мобильное приложение On Russia
Мобильное приложение On Russia CryptoBox. Применение шифрования
CryptoBox. Применение шифрования Адаптивная верстка
Адаптивная верстка Технология автоматизации документооборота
Технология автоматизации документооборота