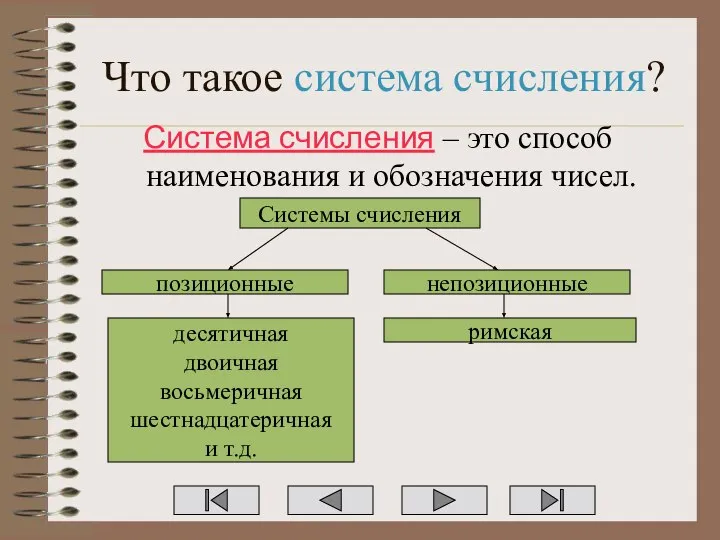
Слайд 2Что такое система счисления?
Система счисления – это способ наименования и обозначения чисел.
Слайд 3Цифра. Что это?
Знаки (символы), используемые в СС для обозначения чисел, называются цифрами.

Слайд 4Римская система счисления
Не является позиционной, т.е. каждый символ обозначает всегда одно и

тоже число;
Цифры обозначаются латинскими буквами:
I, V, X, L, C, D, M
(1, 5, 10, 50, 100, 500, 1000)
Например: XXX – 30; XLI - 41
Слайд 5Позиционные системы счисления
Основанием системы может быть любое натуральное число, большее единицы;
Основание ПСС

– это количество цифр, используемое для представления чисел;
Значение цифры зависит от ее позиции, т.е. одна и та же цифра соответствует разным значениям в зависимости от того, в какой позиции числа она стоит;
Например: 888: 800; 80; 8
Любое позиционное число можно представить в виде суммы степеней основания системы.
Слайд 6Десятичная СС
Основание системы – число 10;
Содержит 10 цифр: 0, 1, 2, 3,

4, 5, 6, 7, 8, 9;
Любое десятичное число можно представить в виде суммы степеней числа 10 – основания системы;
Слайд 7Двоичная СС
Основание системы – 2;
Содержит 2 цифры: 0; 1;
Любое двоичное число можно

представить в виде суммы степеней числа 2 – основания системы;
Примеры двоичных чисел: 11100101; 10101;
Слайд 8Правила перехода
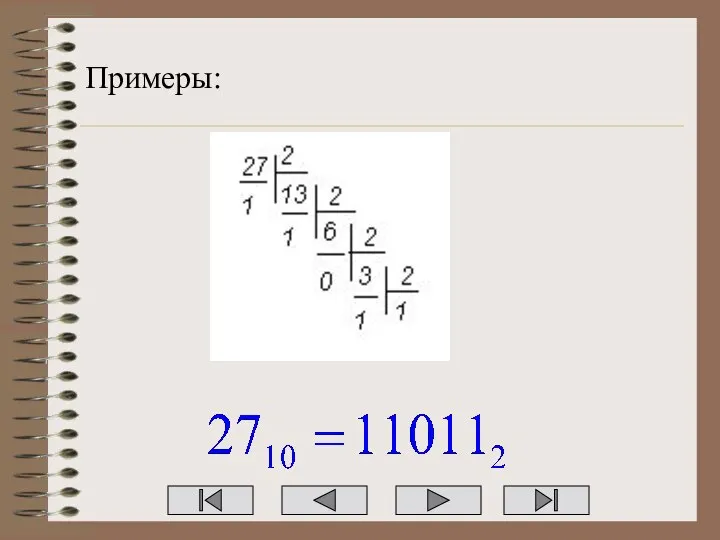
Из десятичной СС в двоичную СС:
Разделить десятичное число на 2. Получится

частное и остаток.
Частное опять разделить на 2. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 2.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет двоичной записью исходного десятичного числа.
Слайд 10Задание № 1:
Для десятичных чисел 341; 125; 1024; 4095 выполни перевод в

двоичную систему счисления.
проверка
Слайд 112. Правило перехода из двоичной системы счисления в десятичную.
Для перехода из двоичной

системы счисления в десятичную необходимо двоичное число представить в виде суммы степеней двойки и найти ее десятичное значение.
Пример:
Слайд 12Задание № 2:
Двоичные числа 1011001, 11110, 11011011 перевести в десятичную систему.
проверка

Слайд 13Восьмеричная СС
Основание системы – 8;
Содержит 8 цифры: 0; 1; 2; 3; 4;

5; 6; 7;
Любое восьмеричное число можно представить в виде суммы степеней числа 8 – основания системы;
Примеры восьмеричных чисел: 2105; 73461;
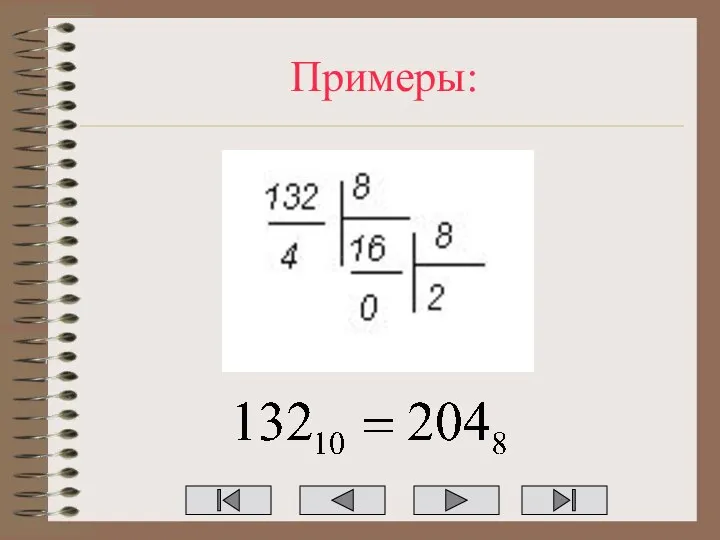
Слайд 14Правило перехода из десятичной системы счисления в восьмеричную
Разделить десятичное число на 8.

Получится частное и остаток.
Частное опять разделить на 8. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 8.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет восьмеричной записью исходного десятичного числа.
Слайд 16Задание № 3:
Десятичные числа 421, 5473, 1061 перевести в восьмеричную систему.
проверка

Слайд 17Правило перехода из восьмеричной системы счисления в десятичную.
Для перехода из восьмеричной системы

счисления в десятичную необходимо восьмеричное число представить в виде суммы степеней восьмерки и найти ее десятичное значение.
Слайд 18Задание № 4:
Восьмеричные числа 41, 520, 306 перевести в десятичную систему.
проверка

Слайд 19Шестнадцатеричная СС
Основание системы – 16;
Содержит 16 цифр: от 0 до 9; A;

B; C; D; E; F;
Любое шестнадцатеричное число можно представить в виде суммы степеней числа 16 – основания системы;
Примеры шестнадцатеричных чисел: 21AF3; B09D;
Слайд 20Правило перехода из десятичной системы счисления в шестнадцатеричную
Разделить десятичное число на 16.

Получится частное и остаток.
Частное опять разделить на 16. Получится частное и остаток.
Выполнять деление до тех пор, пока последнее частное не станет меньшим 16.
Записать последнее частное и все остатки в обратном порядке. Полученное число и будет шестнадцатеричной записью исходного десятичного числа.
Слайд 22Задание № 5:
Десятичные числа 512, 302, 2045 перевести в шестнадцатеричную систему.
проверка

Слайд 23Правило перехода из шестнадцатеричной системы счисления в десятичную.
Для перехода из шестнадцатеричной системы

счисления в десятичную необходимо шестнадцатеричное число представить в виде суммы степеней шестнадцати и найти ее десятичное значение.
Слайд 24Задание № 6:
Шестнадцатеричные числа B5, A28,CD перевести в десятичную систему.
проверка

Слайд 26Правило перехода из двоичной системы счисления в восьмеричную
Разбить двоичное число на классы

справа налево по три цифры в каждом. Заменить каждый класс соответствующей восьмеричной цифрой.
Слайд 27Задание № 7:
Двоичные числа 10101111, 11001100110 перевести в восьмеричную систему
проверка

Слайд 28Правило перехода из восьмеричной системы счисления в двоичную
Каждую восьмеричную цифру заменить двоичным

классом по три цифры в каждом
Слайд 29Задание № 8:
Восьмеричные числа 26, 702, 4017 перевести в двоичную систему.
проверка

Слайд 30Правило перехода из двоичной системы счисления в шестнадцатеричную
Разбить двоичное число на классы

справа налево по четыре цифры в каждом. Заменить каждый класс соответствующей шестнадцатеричной цифрой.
Слайд 31Задание № 9:
Двоичные числа 10101111, 11001100110 перевести в шестнадцатеричную систему
проверка

Слайд 32Правило перехода из шестнадцатеричной системы счисления в двоичную
Каждую шестнадцатеричную цифру заменить двоичным
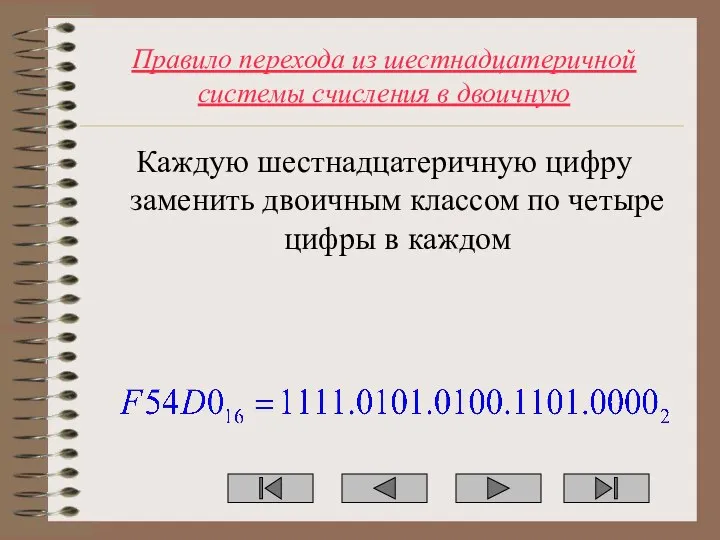
классом по четыре цифры в каждом
Слайд 33Задание № 10:
Шестнадцатеричные числа C3, B096, E38 перевести в двоичную систему.
проверка

Слайд 34Задания для домашней работы
Для каждого из чисел: 12310, 45610 выполнить перевод: 10→2,

10 → 8, 10 → 16.
Для каждого из чисел: 1000112, 1010010112, 11100100012 выполнить перевод: 2 → 10, 2 → 8, 2 → 16.
Для чисел: 543218, 545258, 7778, 1AB16, A1B16, E2E416, E7E516 выполнить соответствующий перевод: 8 → 2, 16 → 2.





















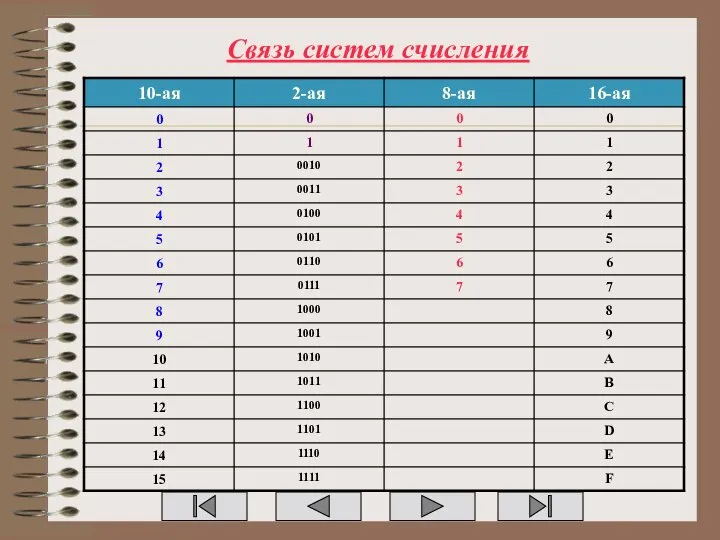


















 Обработка информации
Обработка информации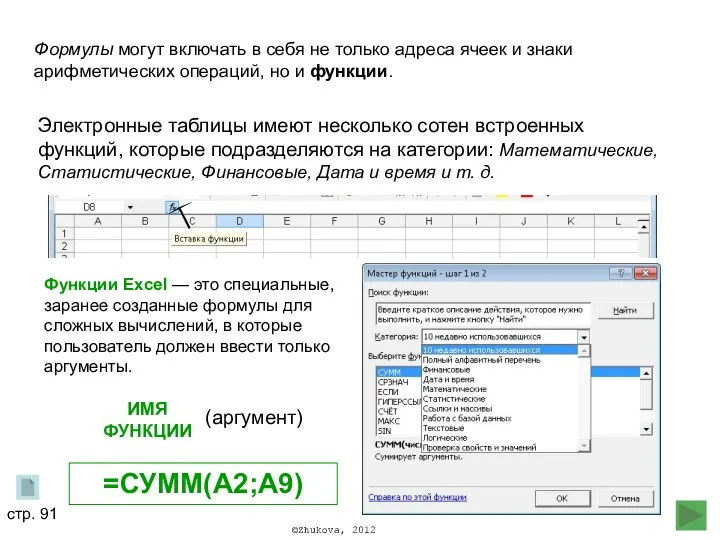 Электронные таблицы
Электронные таблицы Создание и разработка мобильной игры
Создание и разработка мобильной игры Основные понятия информационных систем, банков и баз данных. Виды учетов в ОВД
Основные понятия информационных систем, банков и баз данных. Виды учетов в ОВД Любая достаточно развитая технология неотличима от магии. Третий закон Артура Кларка
Любая достаточно развитая технология неотличима от магии. Третий закон Артура Кларка ТехникаБезопасности (1)
ТехникаБезопасности (1) Разработка бренд айдентики и позиционирования центра социологических исследований
Разработка бренд айдентики и позиционирования центра социологических исследований Интерактивная система голосования VOTUM
Интерактивная система голосования VOTUM Комплекс лабораторных работ по дисциплине Технические и аудиовизуальные технологии обучения
Комплекс лабораторных работ по дисциплине Технические и аудиовизуальные технологии обучения Дизайн. Творческий мир социальных сетей. Создание артов
Дизайн. Творческий мир социальных сетей. Создание артов Мовиус — это система автоматической продажи билетов в соответствии с ФЗ-54
Мовиус — это система автоматической продажи билетов в соответствии с ФЗ-54 Знаковые модели. Моделирование и формализация
Знаковые модели. Моделирование и формализация Компьютерные сети
Компьютерные сети Программа, рассчитывающая сколько нужно пройти для того, чтобы сбросить определенное количество калорий
Программа, рассчитывающая сколько нужно пройти для того, чтобы сбросить определенное количество калорий Мини-Мани: полезные ресурсы. Интернет в помощь финансовому образованию
Мини-Мани: полезные ресурсы. Интернет в помощь финансовому образованию Представление информации
Представление информации Одномерные массивы целых чисел. Начала программирования
Одномерные массивы целых чисел. Начала программирования Создаем аудогид
Создаем аудогид Разработка и проектное обоснование автоматизированной информационной системы для МДК Обработка отраслевой информации ГБПОУ БППК
Разработка и проектное обоснование автоматизированной информационной системы для МДК Обработка отраслевой информации ГБПОУ БППК Интернет-агентство
Интернет-агентство Информация для регистрации на mos.ru
Информация для регистрации на mos.ru Мобильное кино
Мобильное кино Информационная система Учет нерозданных/невостребованных РПО
Информационная система Учет нерозданных/невостребованных РПО Информация и её свойства
Информация и её свойства Принципы, методы и свойства информационных и коммуникационных технологий
Принципы, методы и свойства информационных и коммуникационных технологий Глобальная компьютерные сети
Глобальная компьютерные сети Инструкция по регистрации для предварительного голосования
Инструкция по регистрации для предварительного голосования Egov - электронное правительство
Egov - электронное правительство