Системы счисления. (8 класс)

Содержание
Необыкновенная девочка
Понятие и история развития систем счисления
Позиционные и непозиционные системы счисления
2, cистема счисления
Перевод чисел в 2 систему счисления
Перевод чисел из 2 системы счисления в десятичную

Необыкновенная девочка
Ей было 1100 лет
Она в 101 класс ходила
В портфеле по 100 книг носила
Всё это правда,
А не бред
Когда пыля 10 ног,
Она бежала по дороге
За ней всегда бежал щенок
С одним хвостом
Зато 100 – ногий.
И 10 удивлённых глаз
Смотрели в этот мир привычно
Но станет всё совсем обычно
Когда поймете наш рассказ!

Система счисления –– это определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений.

История развития систем счисления
У первобытных народов не существовало развитой системы счисления. Ещё в 19 в. у многих племён Австралии и Полинезии было только два числительных: один и два; сочетания их образовывали числа: 3 — два-один, 4 — два-два, 5 — два-два-один и 6 — два-два-два. О всех числах, больших 6, говорили: “много”, не индивидуализируя их.

Египтяне впервые ввели десятичную систему счисления, правда без позиционного обозначения. В развитии математики в государствах ислама получила распространение десятичная позиционная система счисления с применением нуля, ведущая своё происхождение от индийской математики. Возникновение десятичной системы счисления связано со счётом на пальцах. Имелись системы счисления и с другим основанием: 5, 12 (счёт дюжинами), 20 (следы такой системы сохранились во французском языке, например quatre-vingts, то есть буквально четыре-двадцать, означает 80, 40, 60 и др.

Вавилонские математики широко пользовались созданной ещё шумерами шестидесятеричной позиционной системой счёта; на основе этой системы были составлены различные вычислительные таблицы: деления и умножения чисел, квадратов и кубов чисел и их корней (квадратных и кубических).

Системы счисления анатомического происхождения
Единичная Загнутый палец
Десятичная Пальцы обеих рук
Пятеричная Пальцы одной руки
Двенадцатеричная Фаланги 4 пальцев
Двадцатеричная Пальцы рук и ног
Алфавитные системы счисления
Славянская, Древнеармянская, Древнегрузинская, Древнегреческая (Ионическая)
Прочие
Римская, Вавилонская
«Машинные» системы счисления
Двоичная, Восьмеричная, Шестнадцатеричная

Все системы счисления делятся на две группы
Непозиционные Позиционные
Единичная Десятичная
Алфавитные Двоичная
Римская Восьмеричная
Древнеегипетская Шестнадцатеричная

В непозиционных системах счисления значение (величина) числа определяется как сумма или разность цифр в числе.
Недостатки непозиционных систем счисления
Существует постоянная потребность введения новых знаков для записи больших чисел.
Невозможно представлять дробные и отрицательные числа.
Сложно выполнять арифметические операции, т.к. не существует алгоритмов их выполнения

Перевод чисел в 2, 8, 16 системы счисления
При переводе чисел из десятичной системы счисления в систему с основанием P > 1 обычно используют следующий алгоритм:
1) если переводится целая часть числа, то она делится на P, после чего запоминается остаток от деления. Полученное частное вновь делится на P, остаток запоминается. Процедура продолжается до тех пор, пока частное не станет равным нулю. Остатки от деления на P выписываются в порядке, обратном их получению;
2) если переводится дробная часть числа, то она умножается на P, после чего целая часть запоминается и отбрасывается. Вновь полученная дробная часть умножается на P и т.д. Процедура продолжается до тех пор, пока дробная часть не станет равной нулю.
Целые части выписываются после двоичной запятой в порядке их получения. Результатом может быть либо конечная, либо периодическая двоичная дробь. Поэтому, когда дробь является периодической, приходится обрывать умножение на каком-либо шаге и довольствоваться приближенной записью исходного числа в системе с основанием P.
Перевод чисел из 2, 8, 16 системы счисления.
При переводе чисел из системы счисления с основанием P в десятичную систему счисления необходимо пронумеровать разряды целой части справа налево, начиная с нулевого, и дробной части, начиная с разряда сразу после запятой, слева направо (начальный номер –1). Затем вычислить сумму произведений соответствующих значений разрядов на основание системы счисления в степени, равной номеру разряда. Это и есть представление исходного числа в десятичной системе счисления

В позиционных системах счисления значение цифры зависит от ее места (позиции) в числе, а в непозиционных не зависит.
В позиционной системе счисления один и тот же числовой символ приобретает различные значения (имеет различный вес) в зависимости от позиции.
Каждая позиция соответствует определенной степени основания системы счисления. Основание равно количеству цифр (знаков в алфавите системы счисления) и определяет, во сколько раз отличаются значения одинаковых цифр, стоящих в соседних позициях
Достоинства позиционных систем счисления
Простота выполнения арифметических операций.
Ограниченное количество символов (цифр) для записи любых чисел

Двоичная система счисления

Системы счисления
Системы счисления – это определенные правила записи чисел и связанные с этими правилами способы выполнения вычислений.
Позиционная система – значение цифры определяется её позицией в записи числа.
Позиционная система
Десятичная
Двоичная
Алфавит: 0,1, 2, 3, 4, 5, 6, 7, 8, 9
Основание (количество цифр): 10
47310 =4*100+7*10+3*1=
=4*102+7*101+3*100
Алфавит: 0,1
Основание (количество цифр): 2
1012 =1*22+0*21+1*20
Развернутая форма записи числа

Задание 1:
5 789=
51,89 =
32 478 =
26, 378 =
3*104+2*103+4*102+7*101+8*100
2*101+6*100+3*10-1+7*10-2+8*10-3
5*1000+7*100+8*10+9*1
5*103+7*102+8*101+9*100
5*101+1*100+8*10-1
+9*10-2
5*10+1*1+8*0,1+9*0,01=

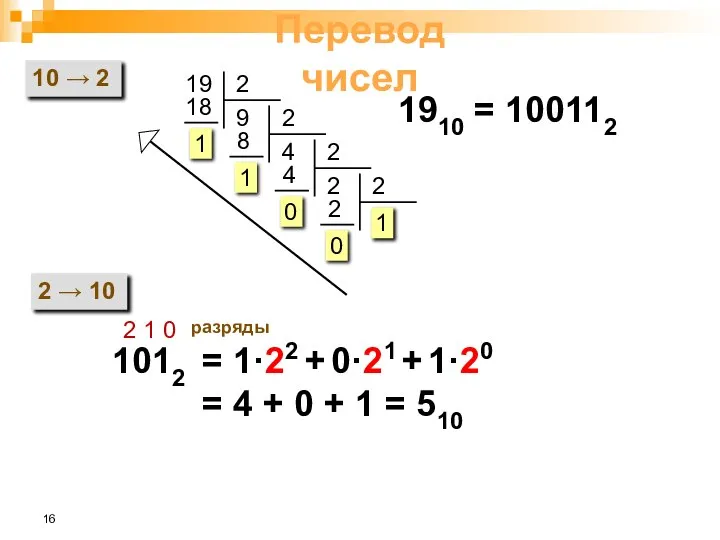
Перевод чисел
10 → 2
19
1
1910 = 100112
2 → 10
1012
2 1 0
разряды
= 1·22 + 0·21 + 1·20
= 4 + 0 + 1 = 510

Примеры:
3710 = ?2
3710 = 1001012
111012 = ?10
111012 =
1*24+1*23+1*22+0*21+1*20=16+8+4+1=2910

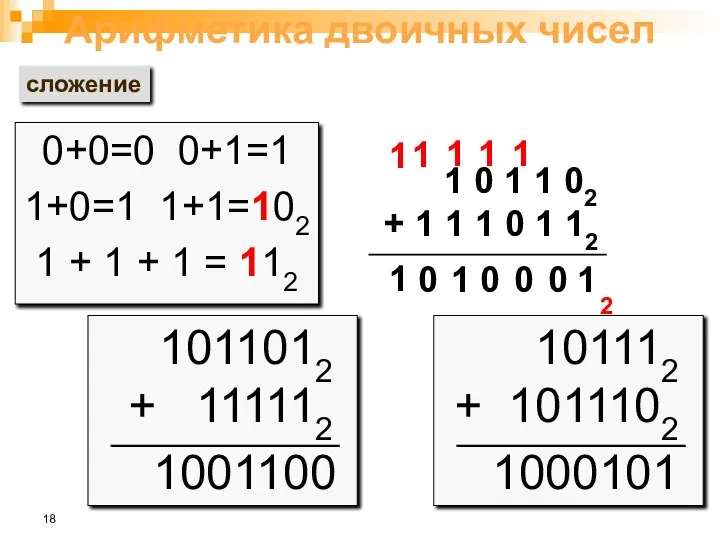
Арифметика двоичных чисел
сложение
0+0=0 0+1=1
1+0=1 1+1=102
1 + 1 + 1 = 112
1 0 1 1 02
+ 1 1 1 0 1 12
1
0
0
0
1
1
0
2
1
1
1
1
1
10011002
10001012

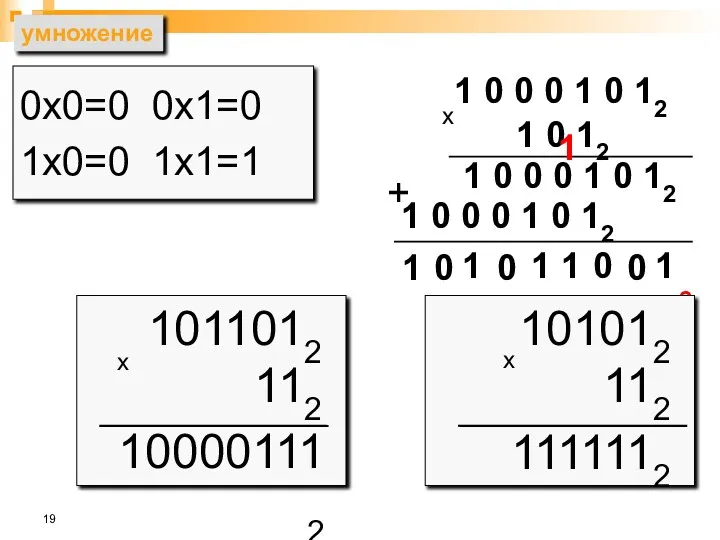
умножение
0х0=0 0х1=0
1х0=0 1х1=1
1 0 0 0 1 0 12
1 0 12
1 0 0 0 1 0 12
х
+
1 0 0 0 1 0 12
1
0
0
1
1
1
0
1
0
1
2
х
х
100001112
1111112