Содержание
- 2. Постановка задачи Пусть в памяти хранится последовательность из n элементов. Такие запросы называют интервальными, потому что
- 3. Терминология
- 4. Классификация задач Если элементы последовательности не изменяются (не предусмотрено выполнение операции модификации элемента), то в названии
- 5. Классификация задач Если сначала все интервальные запросы поступили (после чего они все могли быть проанализированы), а
- 6. Постановка задачи Можно ли это сделать быстрее?
- 7. Постановка задачи Покажем (на примере задач о сумме и минимуме на интервале), что с помощью специальных
- 8. Задача RSQ
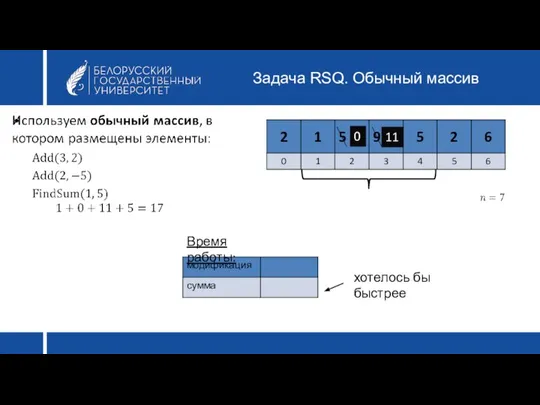
- 9. Задача RSQ. Обычный массив Время работы: хотелось бы быстрее 11 0
- 10. Задача RSQ. Префиксные суммы Выполним предподсчёт
- 11. Задача RSQ. Префиксные суммы Время на запрос суммы:
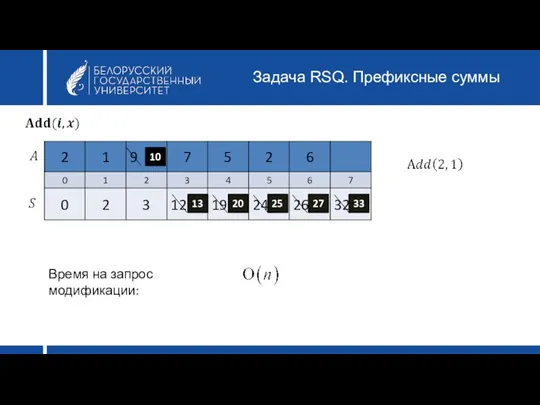
- 12. Задача RSQ. Префиксные суммы Время на запрос модификации: 10 13 20 25 27 33
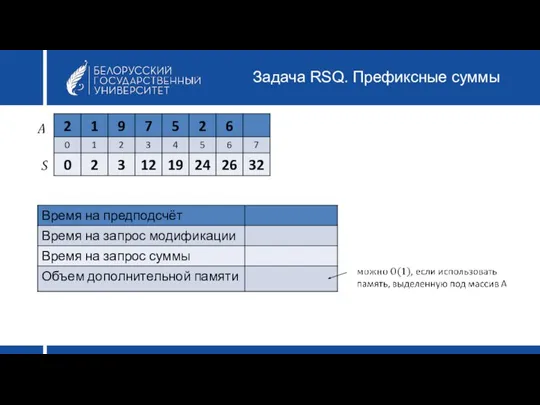
- 13. Задача RSQ. Префиксные суммы
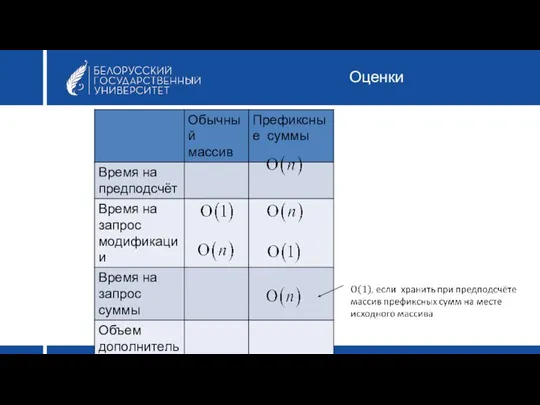
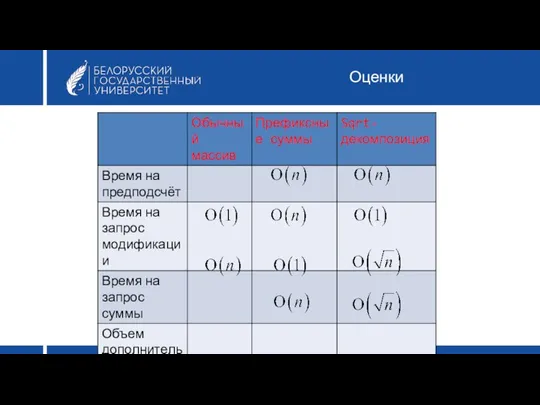
- 14. Оценки
- 15. Промежуточный вариант Одна операция быстрая, вторая медленная Нужно компромиссное решение Модификация Сумма
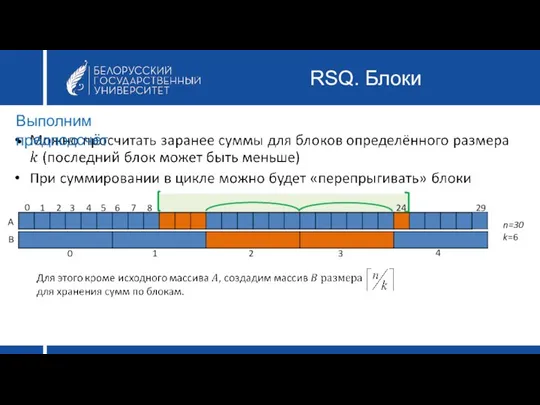
- 16. RSQ. Блоки Выполним предподсчёт A B 0 1 2 3 4 0 1 2 3 4
- 17. RSQ. Блоки Удобно нумеровать блоки с нуля (на рис. размер блока k=6) A B 0 1
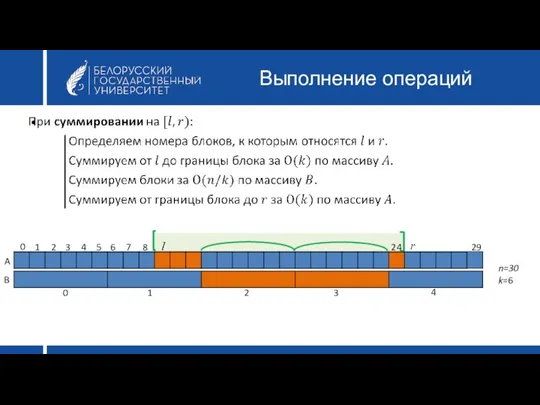
- 18. Выполнение операций A B 0 1 2 3 4 0 1 2 3 4 5 6
- 19. Выполнение операций A B 0 1 2 3 4 0 1 2 3 4 5 6
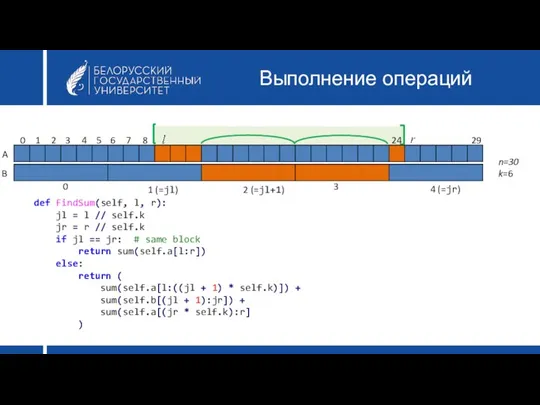
- 20. Выполнение операций A B 0 1 (=jl) 2 (=jl+1) 3 4 (=jr) 0 1 2 3
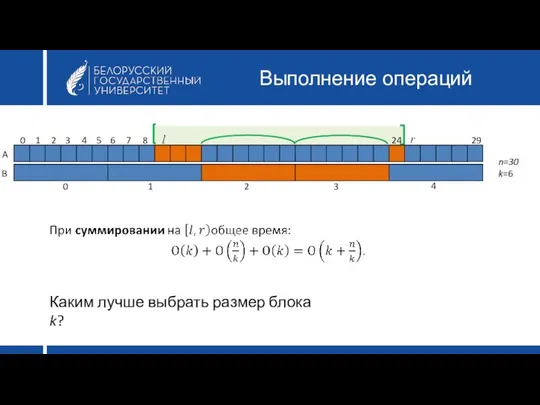
- 21. Выполнение операций A B 0 1 2 3 4 0 1 2 3 4 5 6
- 22. Оптимальный размер блока
- 23. Пример реализации class Summator: def __init__(self, a): self.a = a self.k = floor(sqrt(len(a))) self.b = []
- 24. Оценки
- 25. Дерево отрезков Дальнейшим развитием идеи разбиения на блоки будет следующее:
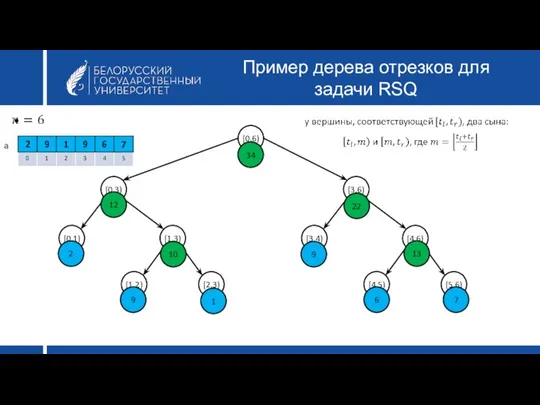
- 26. Пример дерева отрезков для задачи RSQ a 22 6 13 12 10 7 2 9 9
- 27. Дерево отрезков. Число вершин
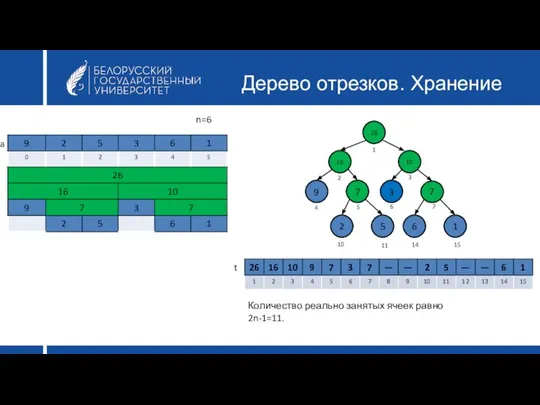
- 28. Дерево отрезков. Хранение Нет необходимости хранить указатели/ссылки Для хранения вершин дерева будем использовать массив (по аналогии
- 29. Дерево отрезков. Хранение 26 16 10 9 7 3 2 5 6 1 1 2 3
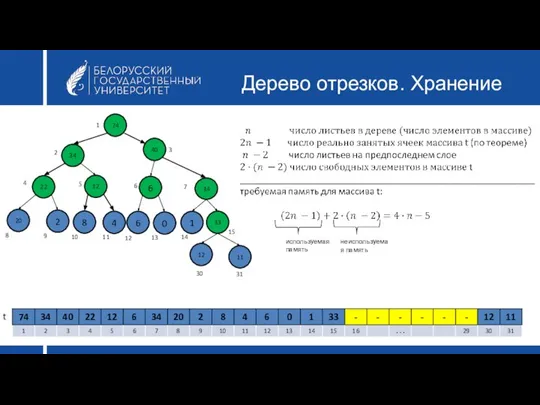
- 30. Дерево отрезков. Хранение 74 34 40 22 12 6 8 4 1 2 3 4 5
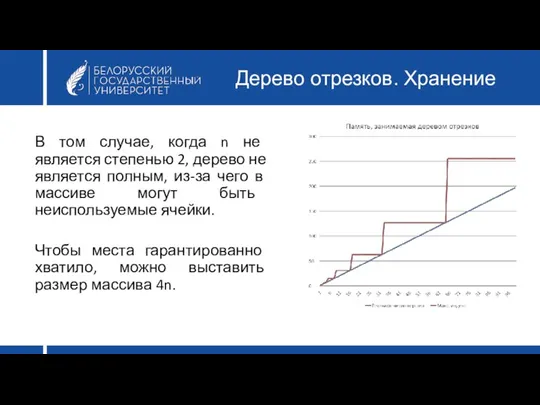
- 31. Дерево отрезков. Хранение В том случае, когда n не является степенью 2, дерево не является полным,
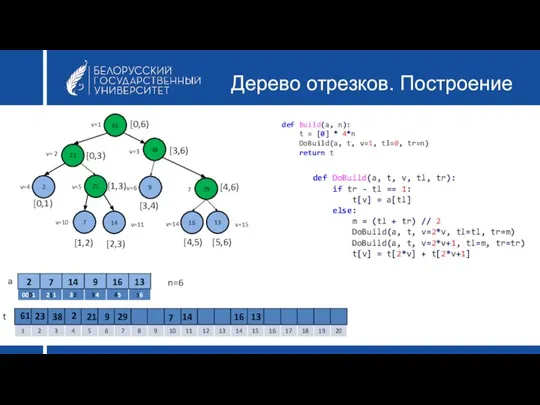
- 32. Дерево отрезков. Построение def DoBuild(a, t, v, tl, tr): if tr - tl == 1: t[v]
- 33. Дерево отрезков. Построение 61 23 38 2 21 9 7 14 v=1 v= 2 v=3 v=4
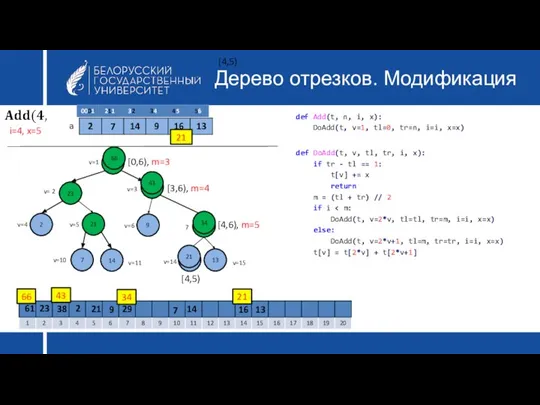
- 34. Дерево отрезков. Модификация def DoAdd(t, v, tl, tr, i, x): if tr - tl == 1:
- 35. Дерево отрезков. Модификация def DoAdd(t, v, tl, tr, i, x): if tr - tl == 1:
- 36. tr tl=m tr=m tl tl tr tl=m tl tr tr=m r l r l l r
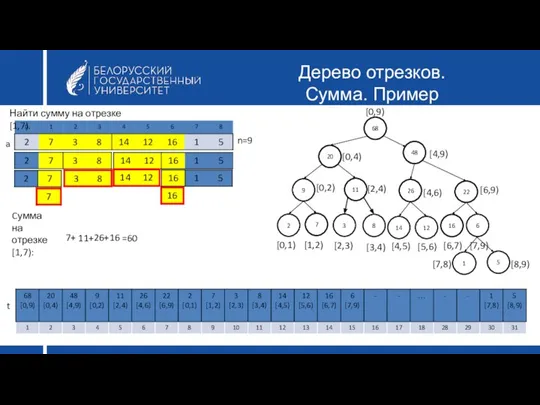
- 37. Дерево отрезков. Сумма. Пример 68 20 48 9 11 26 3 8 t 16 6 22
- 38. Оценка времени работы
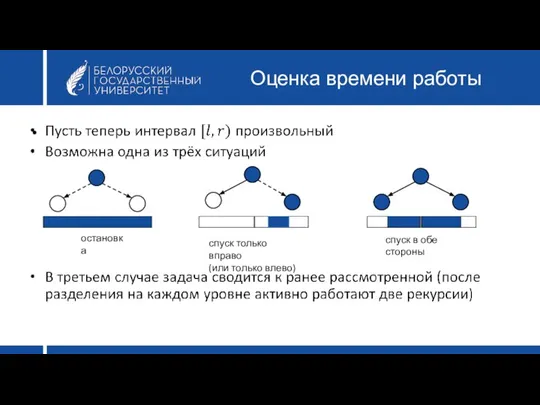
- 39. Оценка времени работы остановка спуск только вправо (или только влево) спуск в обе стороны
- 40. Доработки
- 41. Оценка времени работы
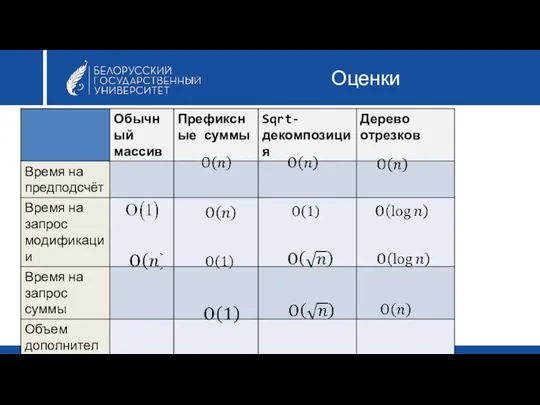
- 42. Оценки
- 43. Статическая задача RMQ Cтатическая online задача RMQ — Range Minimum Query (запрос минимума на отрезке)
- 44. Статическая задача RMQ
- 45. Статическая задача RMQ A Так как каждый элемент таблицы по рекуррентному соотношению T может быть вычислен
- 46. Разрежённая таблица Идея — разреди́ть таблицу, убрать часть информации Будем хранить минимумы для тех интервалов, длины
- 47. Разрежённая таблица
- 48. Sparse table. Пример
- 49. Разрежённая таблица Предположим, что Оценим число «лишних» ячеек в таблице.
- 50. Ответ на запрос
- 51. Ответ на запрос
- 52. Свойства бинарного отношения минимума Ассоциативность (выполнять операции можно в произвольном порядке, т.е. допускается любой порядок расстановки
- 53. Свойства бинарного отношения минимума r a
- 54. Пример 1 1
- 55. Ответ на запрос. Примеры
- 56. Упражнение 1
- 58. Упражнение 2
- 59. Общие задачи 0.2 Задача о сумме (реализация структур для интервальных запросов - сумма на отрезке) iRunner
- 61. Скачать презентацию







































 Системы счисления Определение. Непозиционные и позиционные системы счисления. Развернутая форма записи числа в позиционной сист
Системы счисления Определение. Непозиционные и позиционные системы счисления. Развернутая форма записи числа в позиционной сист Шифрование с использованием закрытого ключа
Шифрование с использованием закрытого ключа Добавление и форматирование текста
Добавление и форматирование текста Development of a traffic analysis system based on neural networks
Development of a traffic analysis system based on neural networks Искусственный интеллект в управлении капиталом
Искусственный интеллект в управлении капиталом Работа в Photoshop. Задание 5
Работа в Photoshop. Задание 5 Автоматизация систем регулирования трафика на перекрестках
Автоматизация систем регулирования трафика на перекрестках Язык программирования Python. Основные встроенные модули
Язык программирования Python. Основные встроенные модули Формирование цвета в системах цветопередачи RGB, CMYK
Формирование цвета в системах цветопередачи RGB, CMYK Веселая информатика
Веселая информатика Введение в математическое моделирование машин
Введение в математическое моделирование машин Проверки моделей и чертежей Siemens PLM Software
Проверки моделей и чертежей Siemens PLM Software История компьютерного пиратства и ситем защиты информации
История компьютерного пиратства и ситем защиты информации Продвижение учреждения дополнительного образования в социальных сетях
Продвижение учреждения дополнительного образования в социальных сетях История развития вычислительной техники
История развития вычислительной техники Документы на новейших носителях
Документы на новейших носителях Функціональний опис та моделювання систем. Лекція 4
Функціональний опис та моделювання систем. Лекція 4 Файл и файловая система
Файл и файловая система Диджитализация кластера. Обучение сотрудников через WhatsApp
Диджитализация кластера. Обучение сотрудников через WhatsApp Методология процессного подхода ARIS
Методология процессного подхода ARIS Депеши Шнюка
Депеши Шнюка Стриминг через ключ трансляции
Стриминг через ключ трансляции Территориальные классификаторы электронных карт и планов
Территориальные классификаторы электронных карт и планов Информаицонная безопасность
Информаицонная безопасность Структуры хранения данных
Структуры хранения данных Презентація досвіду роботи
Презентація досвіду роботи Старт партнерки
Старт партнерки Контрольная работа. Общие принципы построения ЭВМ
Контрольная работа. Общие принципы построения ЭВМ