Содержание
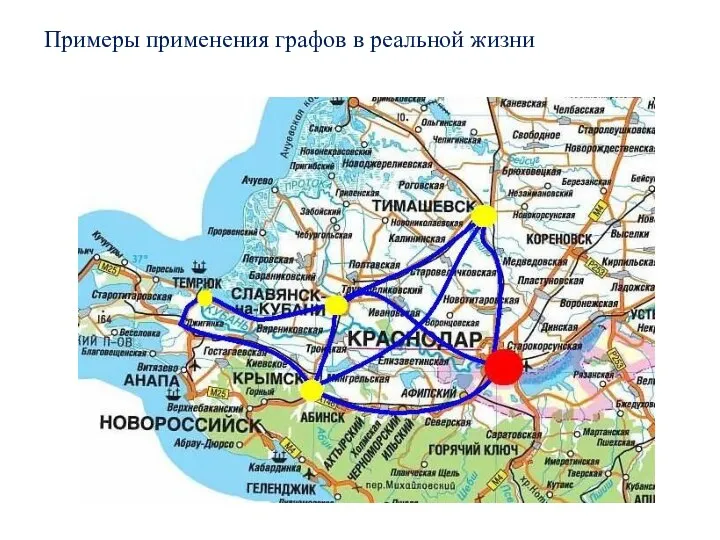
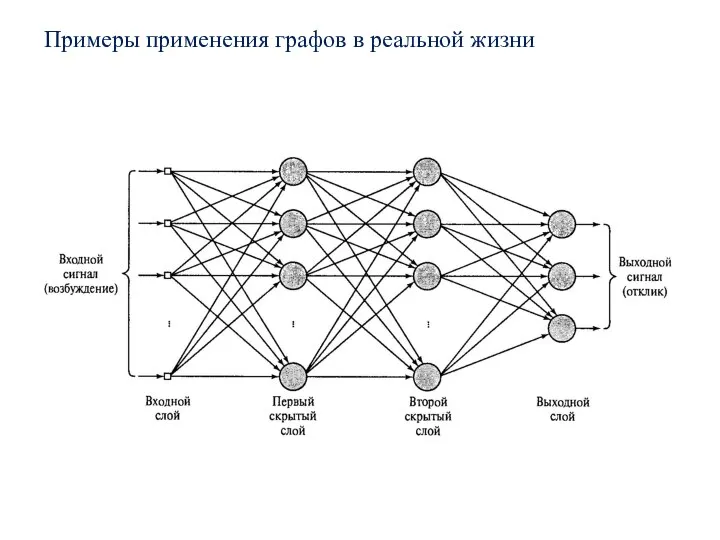
- 2. Примеры применения графов в реальной жизни
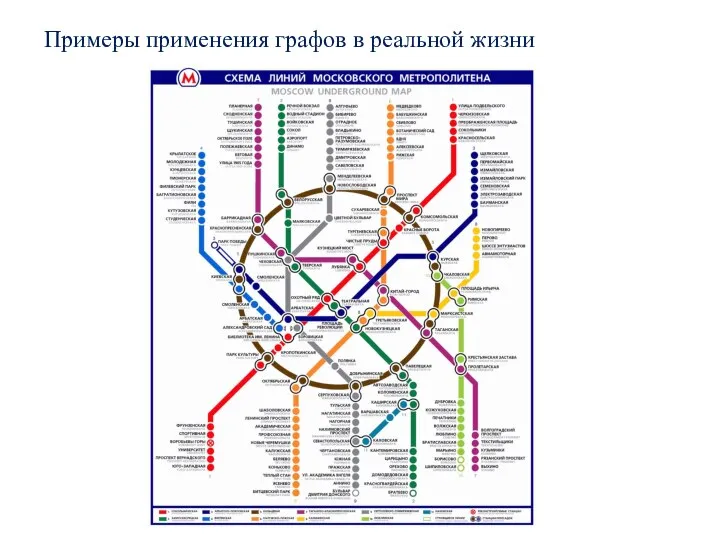
- 3. Примеры применения графов в реальной жизни
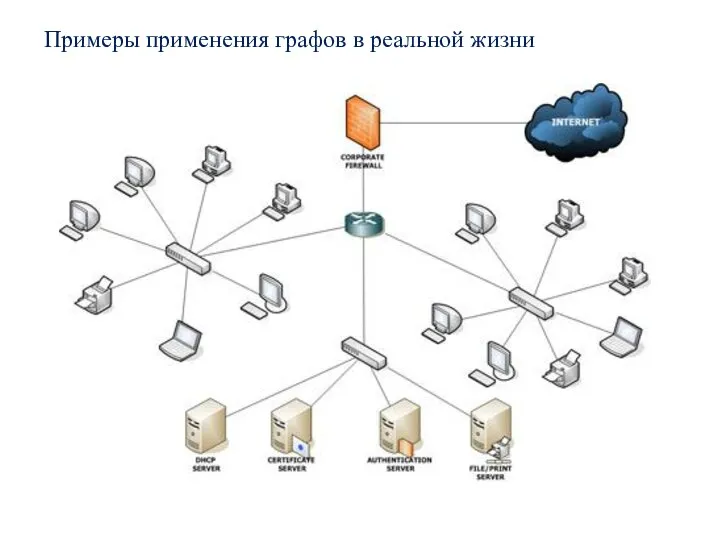
- 4. Примеры применения графов в реальной жизни
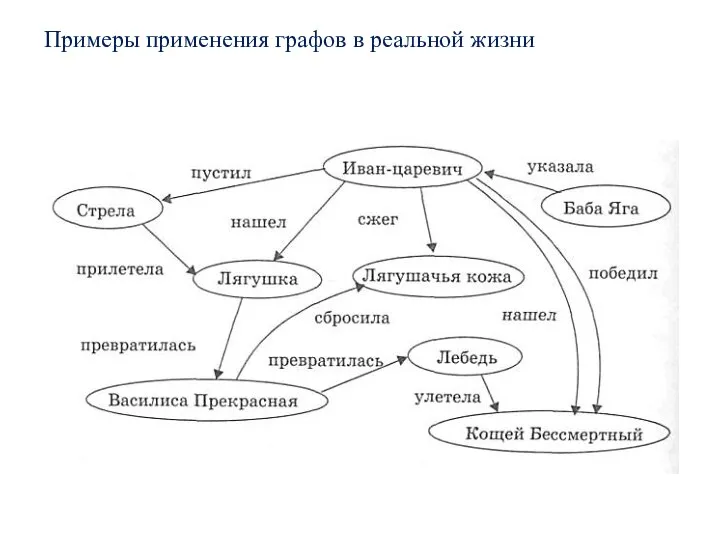
- 5. Примеры применения графов в реальной жизни
- 6. Примеры применения графов в реальной жизни
- 7. Примеры применения графов в реальной жизни
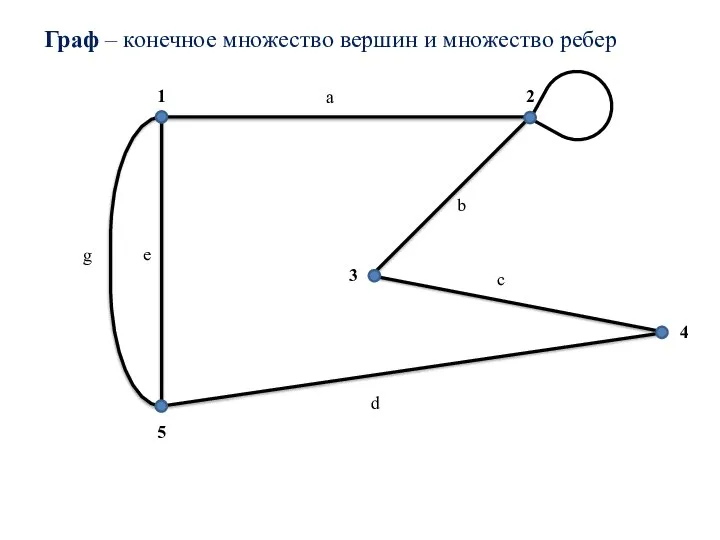
- 8. Граф – конечное множество вершин и множество ребер 1 2 3 4 5 a b c
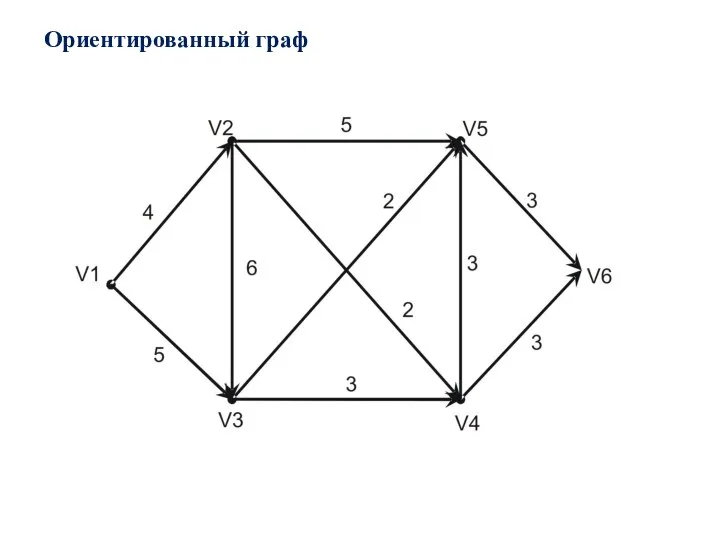
- 9. Ориентированный граф
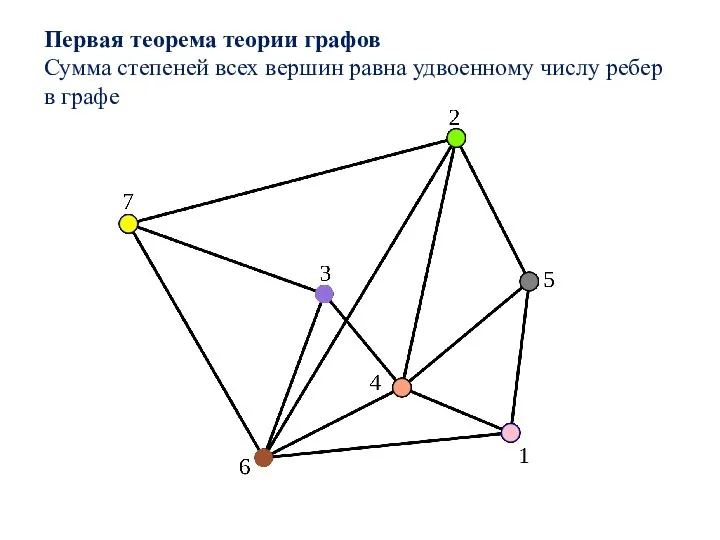
- 10. Первая теорема теории графов Сумма степеней всех вершин равна удвоенному числу ребер в графе
- 11. Задача Найти максимальное число ребер в простом графе, если у него n вершин
- 12. Задача Найти максимальное число ребер в простом графе, если у него n вершин Решение: M –
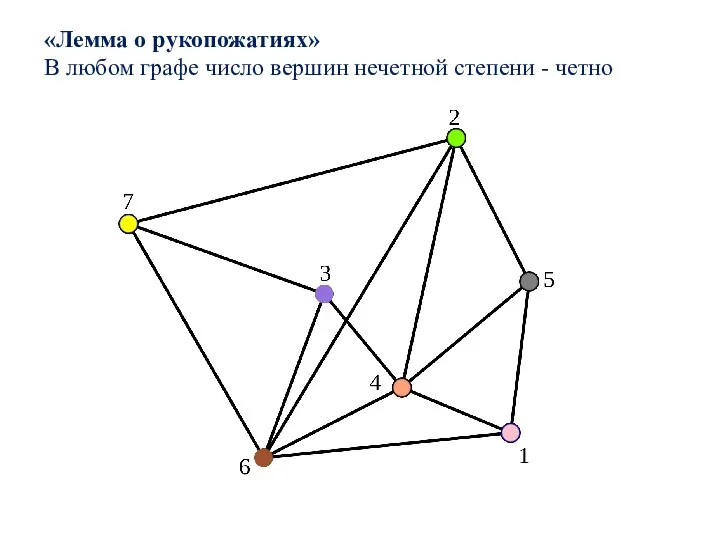
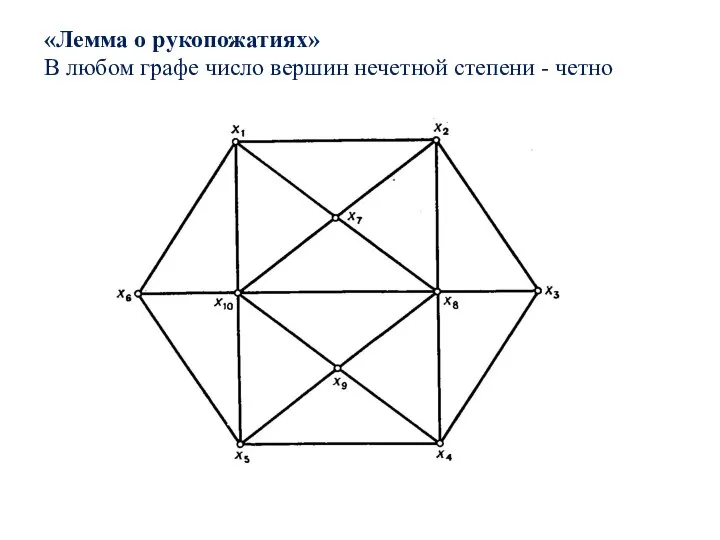
- 13. «Лемма о рукопожатиях» В любом графе число вершин нечетной степени - четно
- 14. «Лемма о рукопожатиях» В любом графе число вершин нечетной степени - четно
- 15. Задача Какая из представленных числовых последовательностей может быть последовательностью степеней вершин графа 2 2 2 1
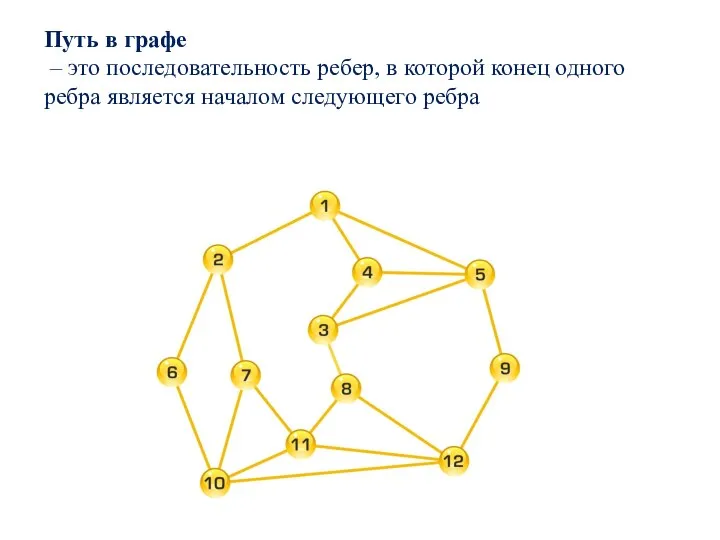
- 16. Путь в графе – это последовательность ребер, в которой конец одного ребра является началом следующего ребра
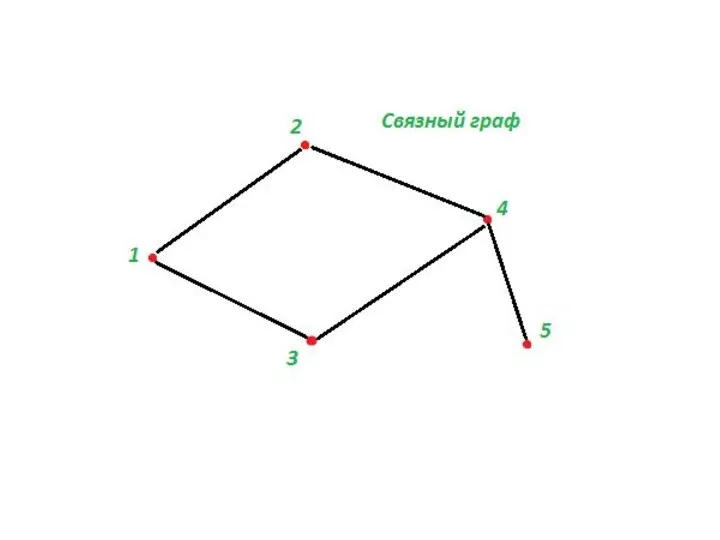
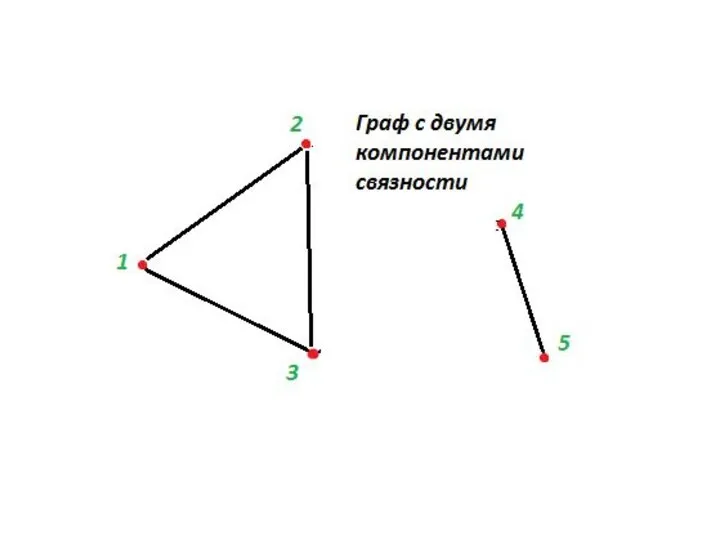
- 17. Связный граф Граф называется связным если между любыми двумя его вершинами существует маршрут. В противном случае
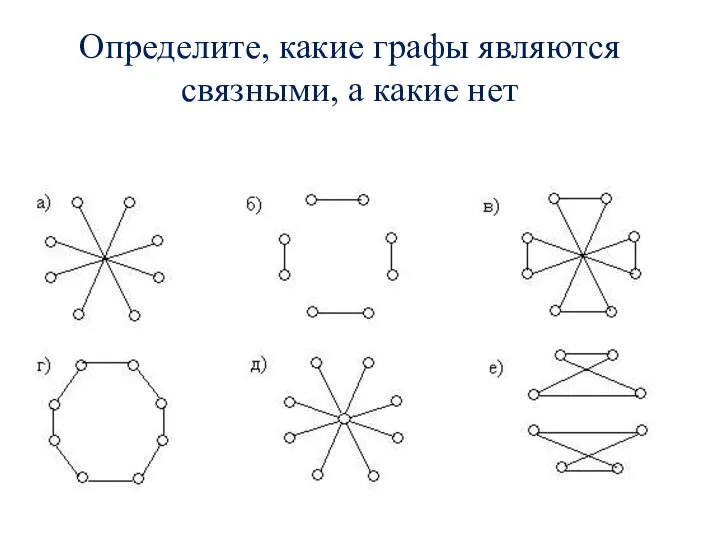
- 20. Определите, какие графы являются связными, а какие нет
- 21. Способы задания графа в памяти ПК
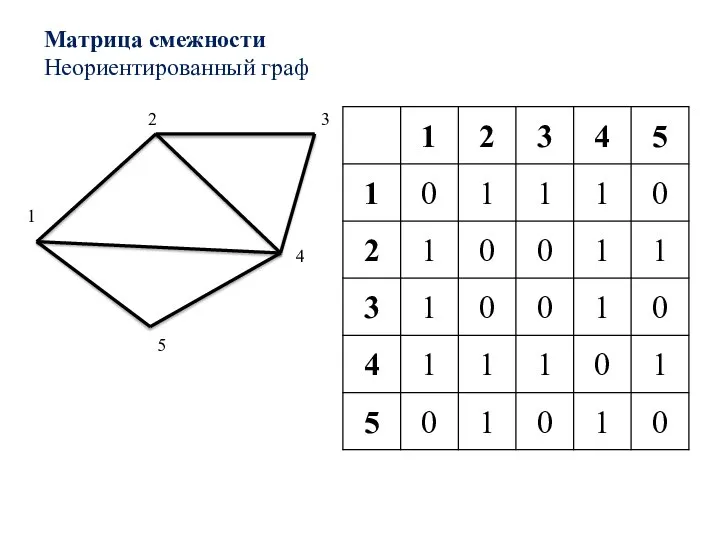
- 22. Матрица смежности Неориентированный граф
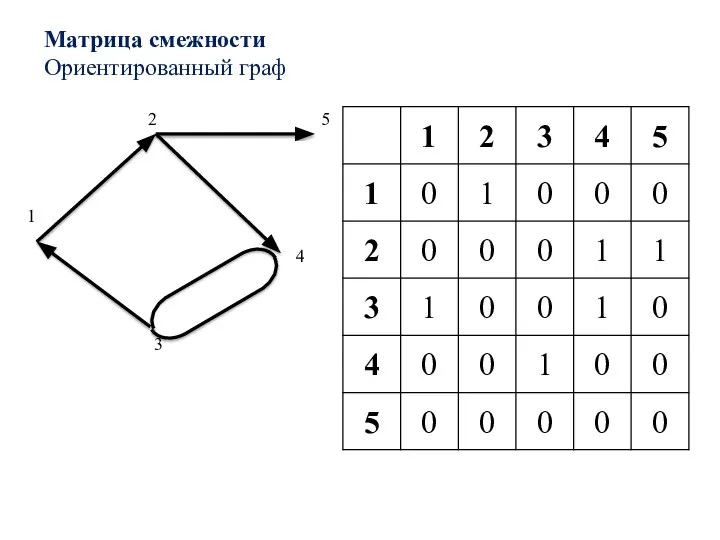
- 23. Матрица смежности Ориентированный граф 1 2 5 4 3
- 24. Списки смежности Для каждой вершины хранится список w[i] смежных с ней вершин 1 2 3 4
- 25. Способы задания графа в Python
- 26. Задача №1 к §45 Напишите программу, которая строит списки смежности для каждой вершины графа на основе
- 27. n=int(input()) ms=[[0] * n for i in range(n)] for i in range(n): m=map(int,input().split()) ms[i]=list(m) for i
- 28. Структуры данных и алгоритмы/Алгоритмы на графах/1. Основные понятия. Способы задания графов В галактике "Milky Way" на
- 29. import numpy as np n=int(input()) ms=[[0] * n for i in range(n)] for i in range(n):
- 30. import numpy as np n=int(input()) ms=[[0] * n for i in range(n)] for i in range(n):
- 32. Задача «Светофорчики» В подземелье M тоннелей и N перекрестков, каждый тоннель соединяет какие-то два перекрестка. Мышиный
- 33. Примеры входные данные 7 10 5 1 3 2 7 1 5 2 7 4 6
- 35. Скачать презентацию






![Списки смежности Для каждой вершины хранится список w[i] смежных с ней вершин](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1166380/slide-23.jpg)


![n=int(input()) ms=[[0] * n for i in range(n)] for i in range(n):](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1166380/slide-26.jpg)

![import numpy as np n=int(input()) ms=[[0] * n for i in range(n)]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1166380/slide-28.jpg)
![import numpy as np n=int(input()) ms=[[0] * n for i in range(n)]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1166380/slide-29.jpg)



 Вопросы начального уровня
Вопросы начального уровня Системы счисления. Математические основы информатики
Системы счисления. Математические основы информатики Перелік функціональності користувача: бачення проекта та концепції
Перелік функціональності користувача: бачення проекта та концепції Арбитраж трафика. Как искать креативы в SPY-сервисе?
Арбитраж трафика. Как искать креативы в SPY-сервисе? Операционной системы компьютера
Операционной системы компьютера Модель взаимодейсвтия: Клиника – МойМедПортал
Модель взаимодейсвтия: Клиника – МойМедПортал Основы создания презентаций
Основы создания презентаций Ведение сайтов. Образовательные программы
Ведение сайтов. Образовательные программы Проектирование реляционной базы данных веб-студии Салавей
Проектирование реляционной базы данных веб-студии Салавей Прикладные протоколы стека FTP и TFTP
Прикладные протоколы стека FTP и TFTP Основы моделирования схем в программе Electronics Workbench 512
Основы моделирования схем в программе Electronics Workbench 512 Организационные процессы жизненного цикла программного средства
Организационные процессы жизненного цикла программного средства Презентация на тему Экстремизм в Интернете
Презентация на тему Экстремизм в Интернете  Практическая работа №2
Практическая работа №2 Computer Networks (lecture 9)
Computer Networks (lecture 9) Одномерные массивы. 10 класс
Одномерные массивы. 10 класс Различные системы счисления
Различные системы счисления Инструкция по обновлению навигационного ПО
Инструкция по обновлению навигационного ПО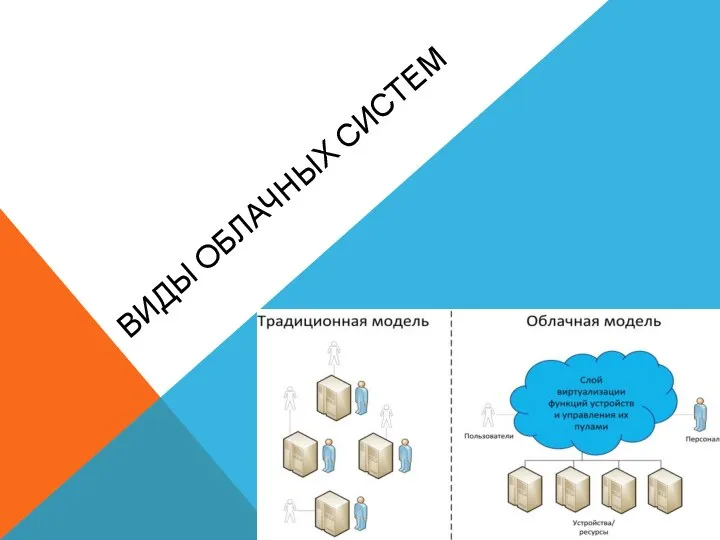 Виды облачных систем
Виды облачных систем Аудит Рекламной Кампании
Аудит Рекламной Кампании Язык программирования Паскаль. Решение задач
Язык программирования Паскаль. Решение задач Что такое машинное обучение
Что такое машинное обучение Диспансеризация взрослого населения
Диспансеризация взрослого населения Презентация на тему Вся правда о компьютерных играх
Презентация на тему Вся правда о компьютерных играх  ContentProvider (Поставщик контента)
ContentProvider (Поставщик контента) Файлы и папки. Ваши данные на компьютере
Файлы и папки. Ваши данные на компьютере Promo Grid e-commerce январь 2019
Promo Grid e-commerce январь 2019 Обзор функциональных возможностей коммутаторов (тема 3)
Обзор функциональных возможностей коммутаторов (тема 3)