Слайд 2АРИФМЕТИКА ЧИСЕЛ С ФИКСИРОВАННОЙ ТОЧКОЙ: УМНОЖЕНИЕ

Слайд 3Умножение
Умножение – это многократно повторенная операция сложения.
Умножение – это нахождение суммы одинаковых

слагаемых в роли которых выступает множимое.
Слайд 4Определение знака произведения
Знак произведения – результат сложения знаковых разрядов по правилам двоичной

арифметики.
Разные знаковые разряды – отрицательное.
1+0=1
0+1=1
Одинаковые – положительное.
0+0=0
1+1=0
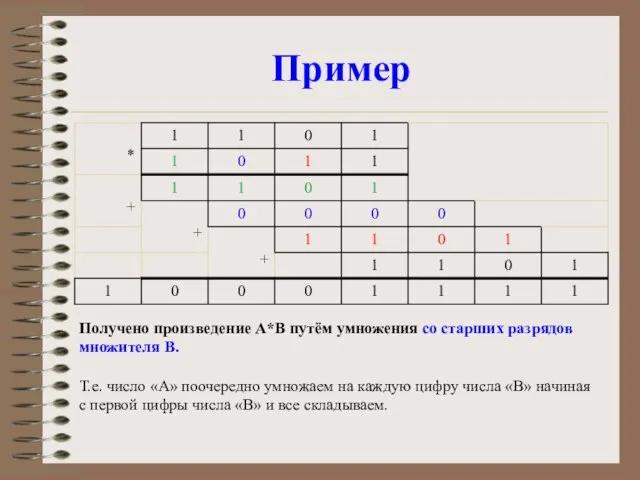
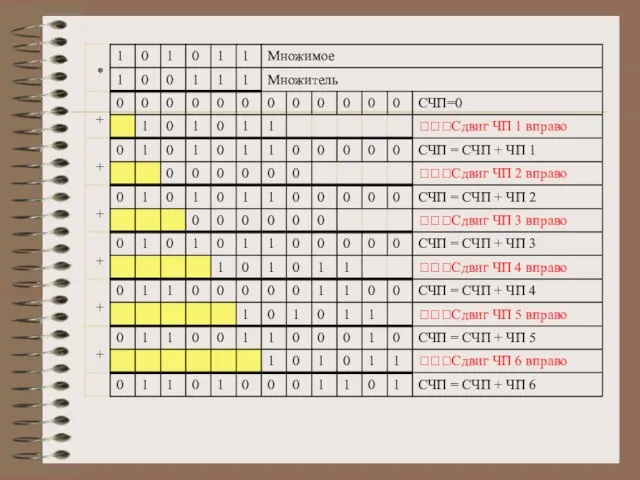
Слайд 6Пример
Получено произведение A*B путём умножения с младших разрядов
множителя B.
Т.е. число «A»

поочередно умножаем на каждую цифру числа «B» начиная
с последней цифры числа «B» и все складываем.
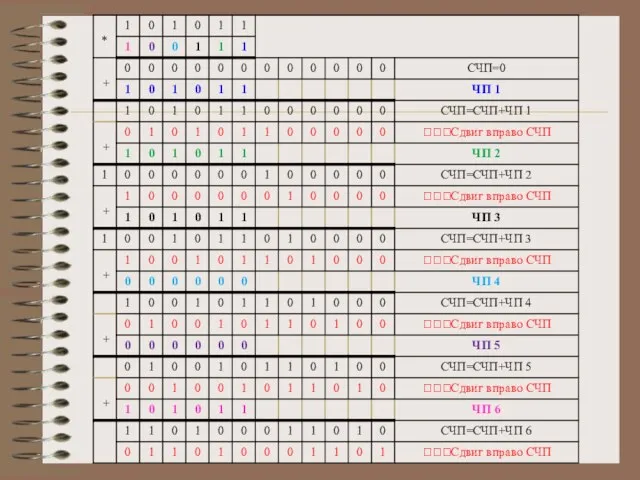
Слайд 7Пример
Получено произведение A*B путём умножения со старших разрядов
множителя B.
Т.е. число «A»
поочередно умножаем на каждую цифру числа «B» начиная
с первой цифры числа «B» и все складываем.
Слайд 10Умножение
Произведение можно получить двумя путями:
Сдвиг множимого на требуемое количество разрядов и добавление

полученного очередного частного произведения к ранее накопленной сумме.
Сдвиг суммы ранее полученных частичных произведений на каждом шаге на один разряд и последующим добавлением к сдвинутой сумме неподвижного множимого, либо 0.
Слайд 11Что такое частичное произведение?

Слайд 12Что такое Сумма Частичных Произведений ?
В начале решения примера сумма частичных произведений

(СЧП) равно 0.
По ходу решения к сумме постоянно прибавляются новые ЧП (частичные
произведения).
Последнее СЧП – это произведение.
Слайд 14Варианты умножения
Основываясь на девятом слайде можно создать четыре варианта схем машинного умножения:
1)

умножение младшими разрядами множителя со сдвигом накапливаемой суммы(СЧП) вправо;
2) умножение младшими разрядами множителя со сдвигом множимого влево;
3) умножение старшими разрядами множителя со сдвигом суммы частичных произведений(СЧП) влево;
4) умножение старшими разрядами множителя со сдвигом множимого вправо.
Слайд 172)
Умножение младшими разрядами множителя со сдвигом множимого влево.
В каждом цикле умножения множимое

сдвигается на один разряд влево и либо складывается с СЧП (при b=1), либо нет (при b=0).
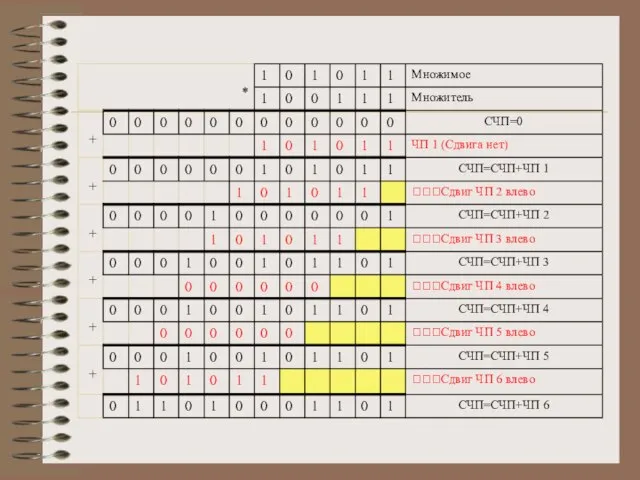
Слайд 193)
Умножение старшими разрядами множителя со сдвигом суммы частичных произведений(СЧП) влево;
Управление умножением будет

производиться цифрами множителя, начиная со старших разрядов. Сумма частичных произведений в каждом цикле будет сдвигаться на один разряд влево.
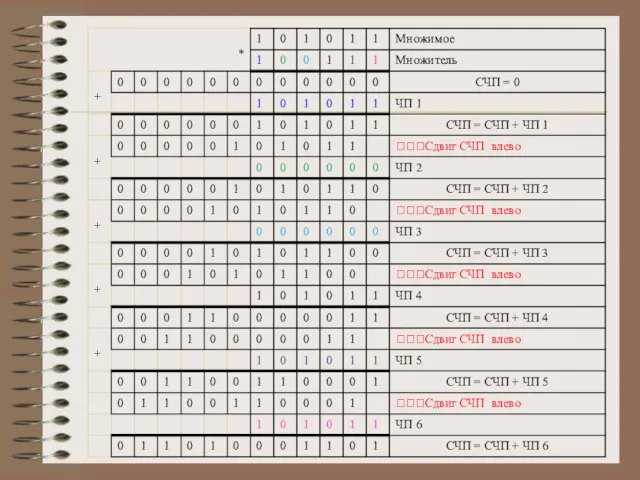
Слайд 214)
Умножение старшими разрядами множителя со сдвигом множимого вправо.
В каждом цикле множимое сдвигается

на один разряд вправо и в зависимости от значения управляющего (старшего) разряда множителя либо передаётся в СЧП, либо нет.
Слайд 24Умножение чисел со знаком
Если надо умножить два числа со знаком, то надо

сначала перемножить их без знака.
А потом определить знак произведения.
(как определить знак произведения показано на следующем слайде).
Слайд 25Определение знака произведения
Знак произведения – результат сложения знаковых разрядов по правилам двоичной

арифметики.
Разные знаковые разряды – отрицательное.
1+0=1
0+1=1
Одинаковые – положительное.
0+0=0
1+1=0




















 Тематический календарь 2020
Тематический календарь 2020 Ядро ОС. Компоненты ОС. Принципы построения ОС
Ядро ОС. Компоненты ОС. Принципы построения ОС Основы разделения сигналов. Тема 4
Основы разделения сигналов. Тема 4 Измерение связи между явлениями или признаками. Корреляция
Измерение связи между явлениями или признаками. Корреляция Введение в инфокоммуникационные системы и сети. Лекция 1
Введение в инфокоммуникационные системы и сети. Лекция 1 Википедия (Wikipedia)
Википедия (Wikipedia) Мобильное программирование. Лекция 7
Мобильное программирование. Лекция 7 Знакомство с Adobe Illustrator. Сфера применения Adobe Illustrator
Знакомство с Adobe Illustrator. Сфера применения Adobe Illustrator Применение и наладка протоколов маршрутизации TCP, UDP, SCTP
Применение и наладка протоколов маршрутизации TCP, UDP, SCTP Билеты 7-9
Билеты 7-9 Информационные объекты
Информационные объекты Приложение лайк
Приложение лайк Система поддержки принятия решений. Электромеханика
Система поддержки принятия решений. Электромеханика ООО Гейзер-телеком. Телекоммуникации под ключ
ООО Гейзер-телеком. Телекоммуникации под ключ Этапы создания сайта. Основы html
Этапы создания сайта. Основы html Взлом социальной сети
Взлом социальной сети Интерактивные форматы и особенности вёрстки в медиа
Интерактивные форматы и особенности вёрстки в медиа Различия синтаксиса С и С++. Тернарные операторы. Ссылки. Файлы
Различия синтаксиса С и С++. Тернарные операторы. Ссылки. Файлы Професия Разработчик
Професия Разработчик Разработка приложения с графическим интерфейсом средствами С# Windows forms
Разработка приложения с графическим интерфейсом средствами С# Windows forms Исполнитель Робот
Исполнитель Робот Архитектура аппаратных средств
Архитектура аппаратных средств Представление информации в форме таблиц
Представление информации в форме таблиц Построение моделей стратиграфии и вертикальных разрезов толщи горного массива по данным геологоразведочных скважин
Построение моделей стратиграфии и вертикальных разрезов толщи горного массива по данным геологоразведочных скважин Анализ программ с циклом
Анализ программ с циклом The increasing use of computers has negative effects
The increasing use of computers has negative effects История ЭВМ
История ЭВМ OOP’s Using JAVA Module 2
OOP’s Using JAVA Module 2