Содержание
- 2. Исторический очерк Термин «нейронная сеть» появился в середине XX века. Первые работы, в которых были получены
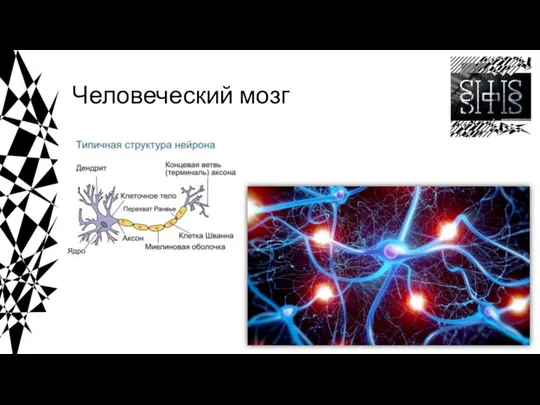
- 3. Человеческий мозг
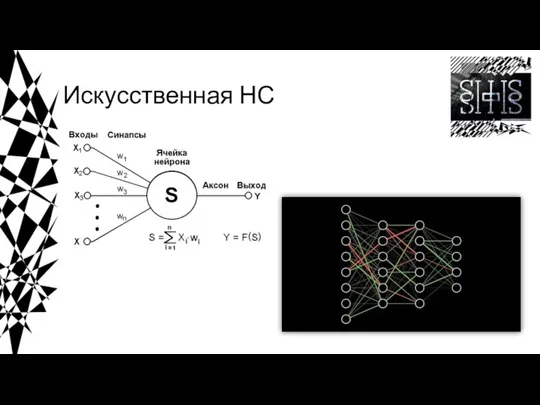
- 4. Искусственная НС
- 5. На пальцах Источник: https://habr.com/post/416211/ Предположим, у нас есть три разных бинарных условия (да или нет) и
- 6. На пальцах Простая модель с тремя вводными и одним выводом. Эта модель может абсолютно отлично работать
- 7. На пальцах То, что вы видите между вводом и выводом — это нейроны. Пока что они
- 8. На пальцах У каждого ввода слева есть значение: 0 или 1, да или нет. Давайте добавим
- 9. На пальцах Цифры, которые мы расставили — это веса связей. Помните, что нейроны — это абстракция?
- 10. На пальцах Ну, вот и все! Нейронка создана, а вы можете ее использовать для любых нужд.
- 11. На пальцах Дальше все просто: вместо одного слоя нейронов мы делаем два и снова все перебираем
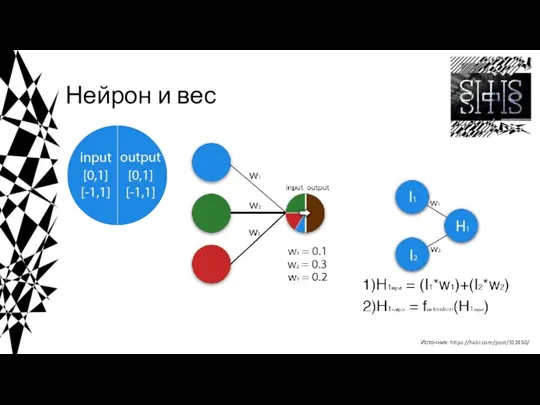
- 12. Нейрон и вес Источник: https://habr.com/post/312450/
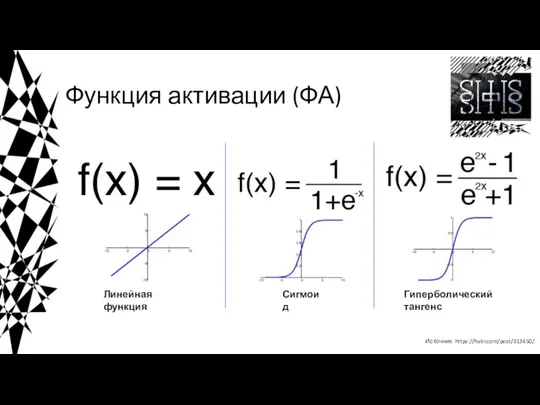
- 13. Функция активации (ФА) Источник: https://habr.com/post/312450/ Линейная функция Сигмоид Гиперболический тангенс
- 14. Эпохи и шаги Источник: https://habr.com/post/416211/ Итерация Это своеобразный счетчик, который увеличивается каждый раз, когда нейронная сеть
- 15. Ошибка Источник: https://habr.com/post/416211/ Ошибка — это процентная величина, отражающая расхождение между ожидаемым и полученным ответами. Ошибка
- 16. Формулы Расчет входа нейрона Правило Видроу-Хоффа для пересчета весов
- 17. Пример. Инициализация Выбираем задачу (Например логическое ИЛИ) Проектируем НС 5. Строим таблицу истинности 6. Выбираем ФА
- 18. Пример. Обучение
- 19. Пример. Обучение
- 20. Пример. Обучение Обучение завершено!
- 21. Пример кода на Python import numpy as np def generate_vectors(): from itertools import product as p
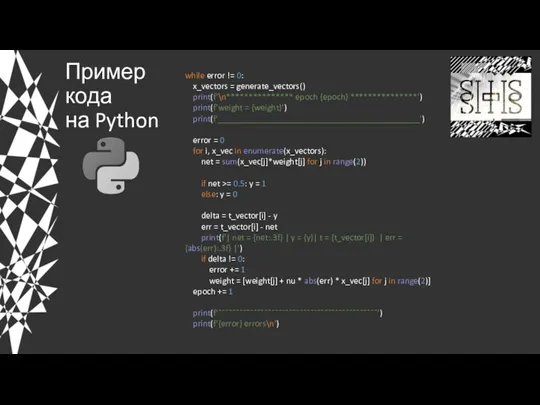
- 22. Пример кода на Python while error != 0: x_vectors = generate_vectors() print(f'\n*************** epoch {epoch} ***************') print(f'weight
- 23. Пример кода на Python *************** epoch 1 *************** weight = [0. 0.] _____________________________________________ | net =
- 24. Персептрон и n-слойные сети Источник: https://habr.com/post/312450/
- 25. Персептрон и n-слойные сети Источник: https://habr.com/post/312450/
- 27. Скачать презентацию
















![Пример кода на Python *************** epoch 1 *************** weight = [0. 0.]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1116664/slide-22.jpg)


 Поиск названия интернет-проекта. Квест-игра
Поиск названия интернет-проекта. Квест-игра Динамические структуры данных
Динамические структуры данных Безопасный интернет. 6 класс
Безопасный интернет. 6 класс Алгоритмы и исполнители
Алгоритмы и исполнители Блокированный жилой дом
Блокированный жилой дом Моделирование и формализация: разработка экономических моделей в среде MS Excel. 10 класс
Моделирование и формализация: разработка экономических моделей в среде MS Excel. 10 класс Мастер класс. Создание сайта
Мастер класс. Создание сайта IDEF (I-CAM DEFinition или Integrated DEFinition) — методологии семейства ICAM
IDEF (I-CAM DEFinition или Integrated DEFinition) — методологии семейства ICAM Скандальные домены
Скандальные домены Формулы, применяющиеся в Excel
Формулы, применяющиеся в Excel Использование электронных образовательных технологий в очном и дистанционном обучении. Документы в облачных хранилищах
Использование электронных образовательных технологий в очном и дистанционном обучении. Документы в облачных хранилищах Роль информационно-коммуникационных технологии в формировании иноязычной коммуникации
Роль информационно-коммуникационных технологии в формировании иноязычной коммуникации Наследование и полиморфизм
Наследование и полиморфизм Защита компьютерной информации
Защита компьютерной информации Наиболее значимые технологии. Геоинформатика
Наиболее значимые технологии. Геоинформатика Возможности сетевого программного обеспечения
Возможности сетевого программного обеспечения Создание сообщества
Создание сообщества Администрирование и методология ведения НСИ. Импорт справочных данных из файла обмена
Администрирование и методология ведения НСИ. Импорт справочных данных из файла обмена Игра в имитацию. Симметричное и асимметричное шифрование
Игра в имитацию. Симметричное и асимметричное шифрование Условные конструкции VBA
Условные конструкции VBA Информация. Тест
Информация. Тест Организация повторений в Паскале
Организация повторений в Паскале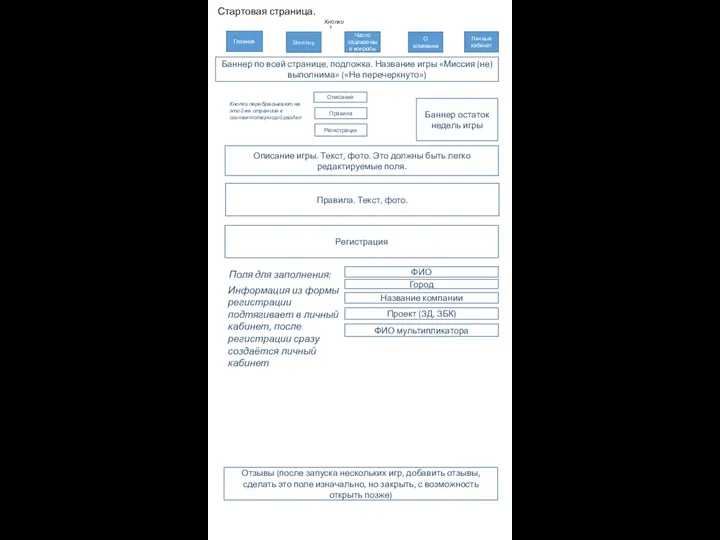 Техническое задание. Игра Миссия (не) выполнима
Техническое задание. Игра Миссия (не) выполнима Учебно-производственный полигон Информационные технологии
Учебно-производственный полигон Информационные технологии Классификация ПО. Системное ПО
Классификация ПО. Системное ПО Процедуры в Turbo Pascalе
Процедуры в Turbo Pascalе Управление проектами в сфере Big Data
Управление проектами в сфере Big Data CodeEvening. Web-разработка
CodeEvening. Web-разработка