Содержание
- 2. Содержание Формальная теория Выводимость в формальной теории Интерпретация Разрешимость Общезначимость Непротиворечивость Полнота и независимость
- 3. Формальная теория множество А символов, образующих алфавит множество слов F в алфавите А, которые называются формулами
- 4. Ограничения (1) Алфавит A может быть конечным или бесконечным Множество формул F обычно задается индуктивно, как
- 5. Ограничения (2) Множество аксиом B может быть конечно или бесконечно Бесконечное множество аксиом B , как
- 6. Свойства формальной теории выводимость интерпретация общезначимость разрешимость непротиворечивость полнота независимость
- 7. Выводимость Пусть - формулы теории Т, т.е. Если существует такое правило вывода R, что , то
- 8. Вывод, гипотеза, теорема Вывод формулы G из формул – – это такая последовательность формул , что
- 9. Интерпретация Интерпретацией формальной теории T в область интерпретации M называется функция, h:F→M, которая каждой формуле F
- 10. Интерпретация Например, припишем значение 0 или 1 атомарным формулам (простым высказываниям), которые входят в сложные, что
- 11. Разрешимость Формальная теория Т называется разрешимой, если существует алгоритм, который для любой формулы теории определяет, является
- 12. Алгоритм Под алгоритмом в интуитивном смысле мы понимает такую последовательность действий, выполнение которых позволяет получить решение
- 13. Свойства алгоритма дискретность шагов детерминируемость регулярность конечность массовость
- 14. Алгоритм Например, правила дорожного движения не являются алгоритмом, т.к. содержат неоднозначность Ярким примером такой неоднозначности может
- 15. Общезначимость Формула общезначима (тавтология), если она истинна в любой интерпретации Формула называется противоречием, если она ложна
- 16. Непротиворечивость Формальная теория семантически непротиворечива, если ни одна из ее теорем не является противоречием Формальная теория
- 18. Скачать презентацию















 Теоремы к зачёту
Теоремы к зачёту По следам теоремы Пифагора
По следам теоремы Пифагора Геометрический биатлон
Геометрический биатлон Комплексные числа
Комплексные числа Решение уравнений. 7 класс
Решение уравнений. 7 класс Основы логистики
Основы логистики Уравнения с двумя переменными
Уравнения с двумя переменными Веселый счет (Счет в прямом и обратном порядке в пределах 10)
Веселый счет (Счет в прямом и обратном порядке в пределах 10) Материал для внеклассной работы по математике. Бедный заяц (сказка)
Материал для внеклассной работы по математике. Бедный заяц (сказка) Числа, кратные 3
Числа, кратные 3 Прямые. Преобразование чертежа прямой. Две прямые
Прямые. Преобразование чертежа прямой. Две прямые Презентация на тему Пределы. Непрерывность функций
Презентация на тему Пределы. Непрерывность функций  Взаимно обратные числа
Взаимно обратные числа Тематические работы в форме ГИА (ЕГЭ)
Тематические работы в форме ГИА (ЕГЭ) Презентация на тему Простейшие задачи в координатах (9 класс)
Презентация на тему Простейшие задачи в координатах (9 класс)  Устный счёт. Закрепление изученного
Устный счёт. Закрепление изученного Презентация на тему Решение систем неравенств (9 класс)
Презентация на тему Решение систем неравенств (9 класс)  Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка
Считаем со смешариками. Тренажер Сложенеие и вычитание в пределах 10.Технологический прием Анимированная сорбонка Квадратные корни
Квадратные корни Математический калейдоскоп. Игра
Математический калейдоскоп. Игра График линейного уравнения с двумя переменными
График линейного уравнения с двумя переменными Регрессионный анализ
Регрессионный анализ Задания с фигурами
Задания с фигурами Второй признак подобия треугольников
Второй признак подобия треугольников Методика изучения Массы
Методика изучения Массы Функции одной и нескольких переменных
Функции одной и нескольких переменных Теория игр
Теория игр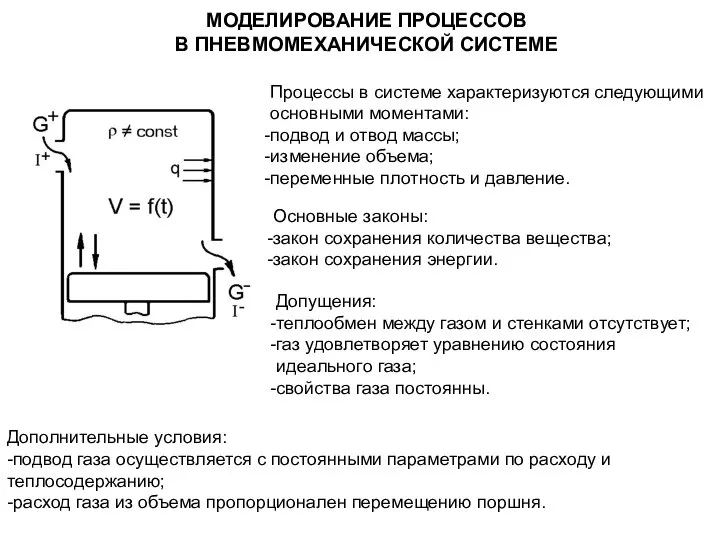 Моделирование процессов в пневмомеханической системе
Моделирование процессов в пневмомеханической системе