аксиомы стереометрии

ГЕОМЕТРИЯ
Планиметрия
Стереометрия
stereos - телесный, твердый, объемный, пространственный
metreo - измерять

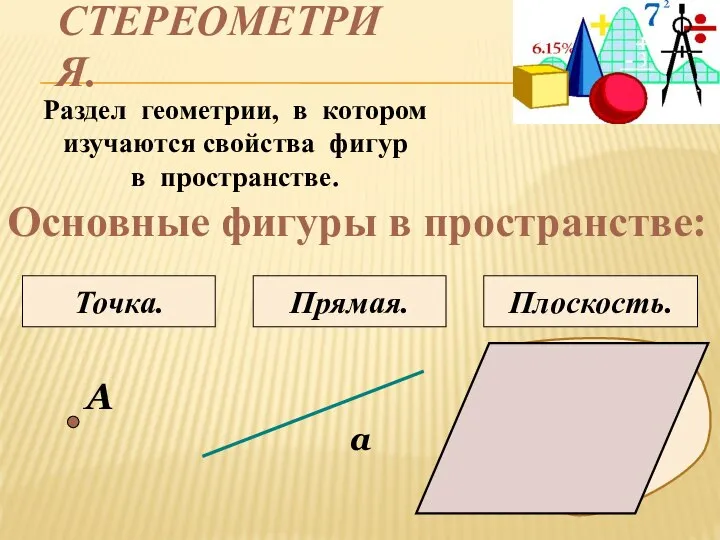
СТЕРЕОМЕТРИЯ.
Раздел геометрии, в котором
изучаются свойства фигур
в пространстве.
Основные фигуры в пространстве:
А
Точка.
а
Прямая.
Плоскость.

Обозначение основных
фигур в пространстве:
точка
прямая
плоскость
A, B, C, …
a, b, c, …
или
AВ, BС, CD, …

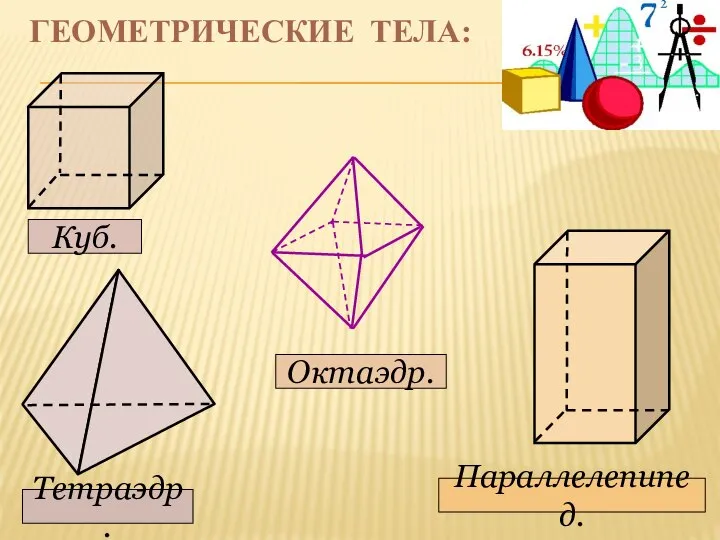
ГЕОМЕТРИЧЕСКИЕ ТЕЛА:
Куб.
Параллелепипед.
Тетраэдр.
Октаэдр.

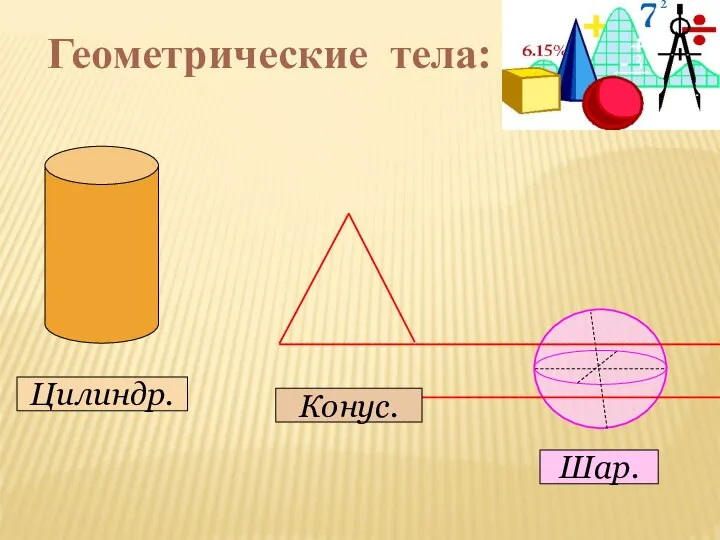
Геометрические тела:
Цилиндр.
Конус.
Шар.

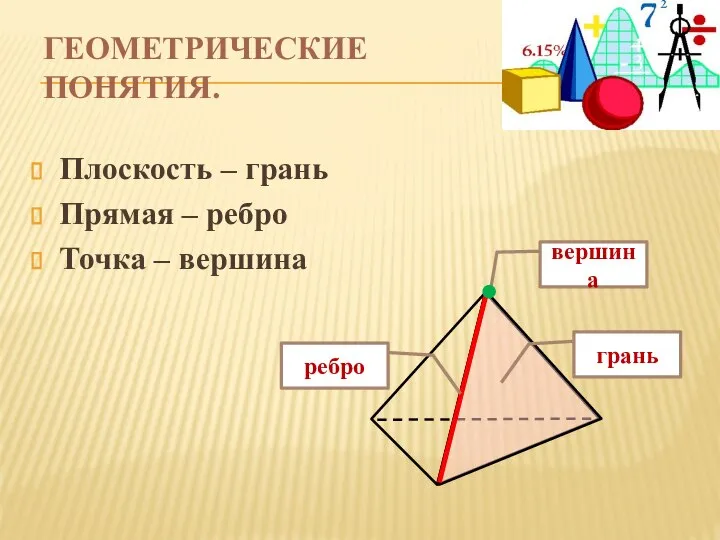
ГЕОМЕТРИЧЕСКИЕ ПОНЯТИЯ.
Плоскость – грань
Прямая – ребро
Точка – вершина
вершина
грань
ребро

АКСИОМА
(от греч. axíõma – принятие положения)
исходное положение научной теории, принимаемое без доказательства

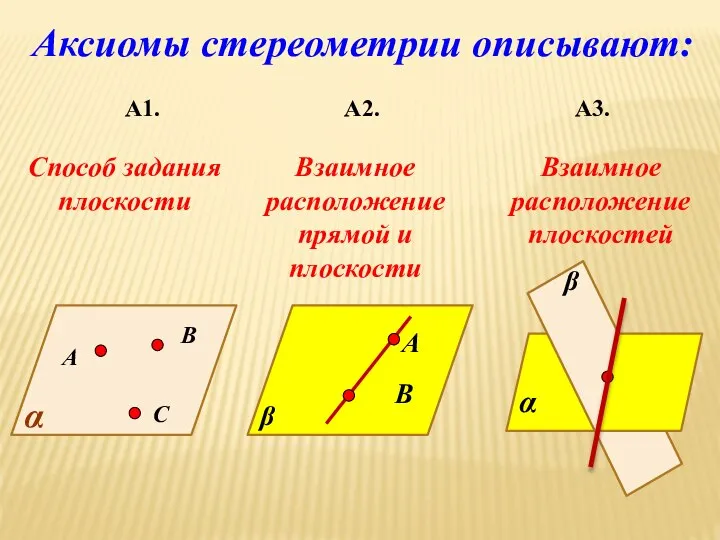
Аксиомы стереометрии.
А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
α
А
В
С

Аксиомы стереометрии.
А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости
α
А
В

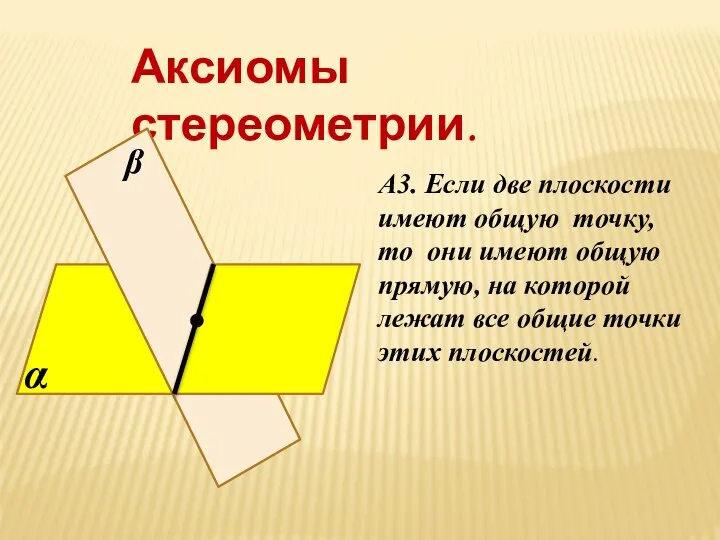
Аксиомы стереометрии.
А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат все общие точки этих плоскостей.
α
β

Аксиомы стереометрии описывают:
А1.
А2.
А3.
А
В
С
α
Способ задания плоскости
β
А
В
Взаимное расположение прямой и плоскости
Взаимное расположение плоскостей
α
β

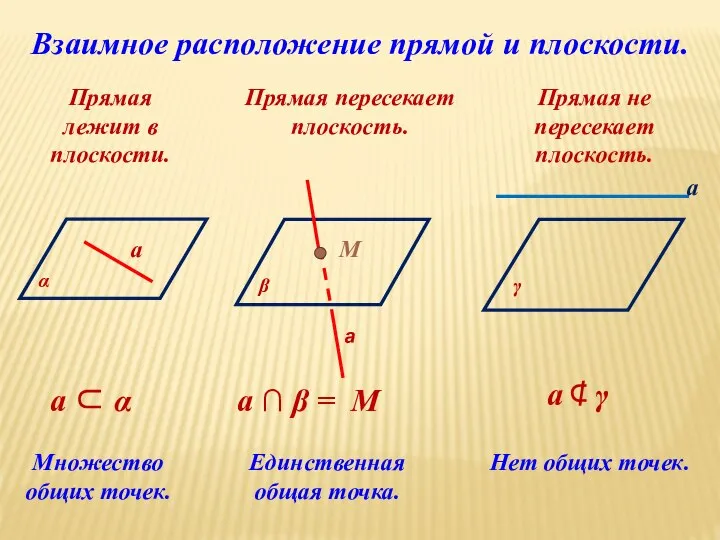
Взаимное расположение прямой и плоскости.
Прямая лежит в плоскости.
Прямая пересекает плоскость.
Прямая не пересекает плоскость.
Множество общих точек.
Единственная общая точка.
Нет общих точек.
α
а
β
а
М
γ
а
а ⊂ α
а ∩ β = М
а ⊄ γ

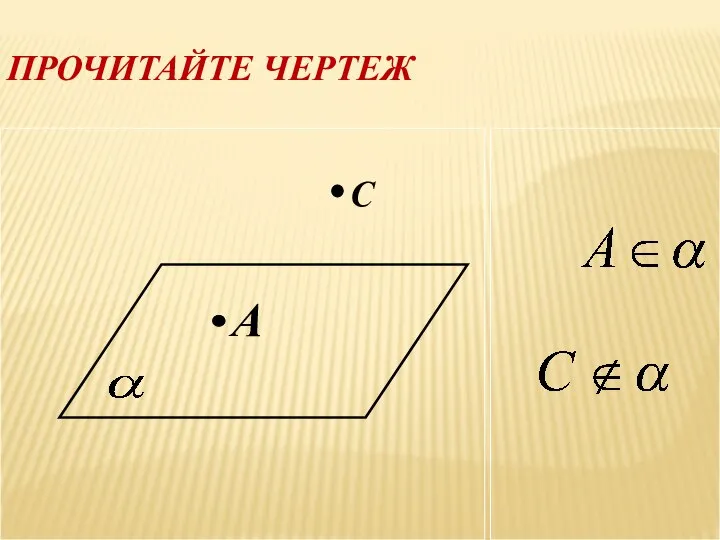
ПРОЧИТАЙТЕ ЧЕРТЕЖ
A
С

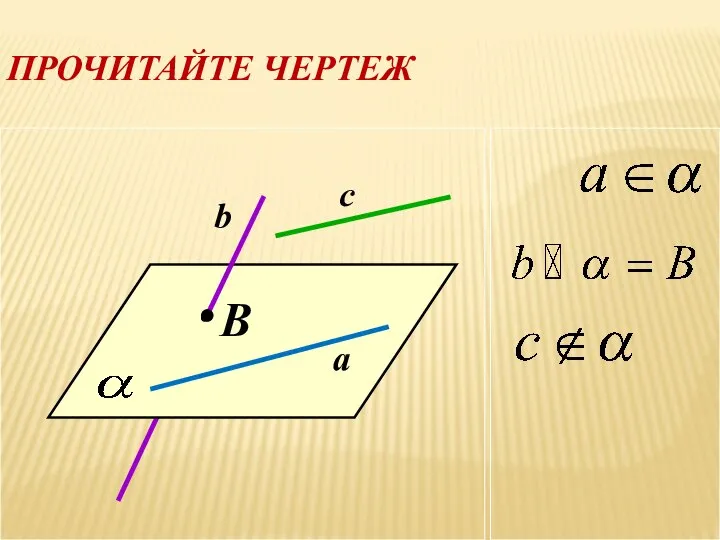
ПРОЧИТАЙТЕ ЧЕРТЕЖ
B
c
b
a

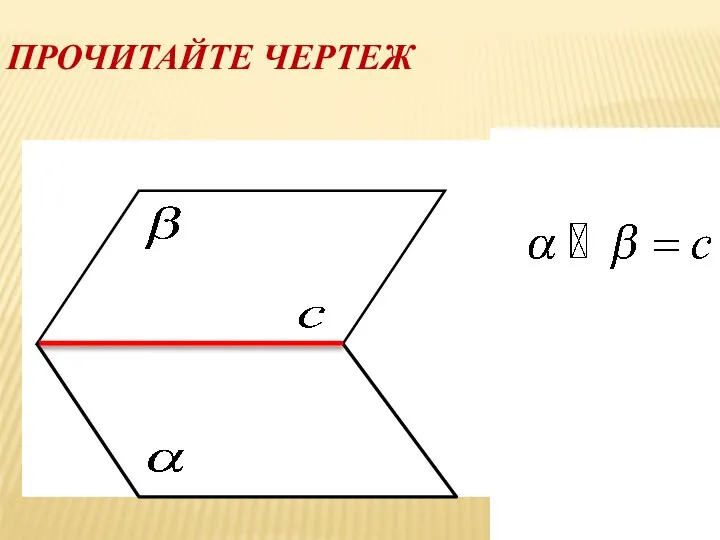
ПРОЧИТАЙТЕ ЧЕРТЕЖ

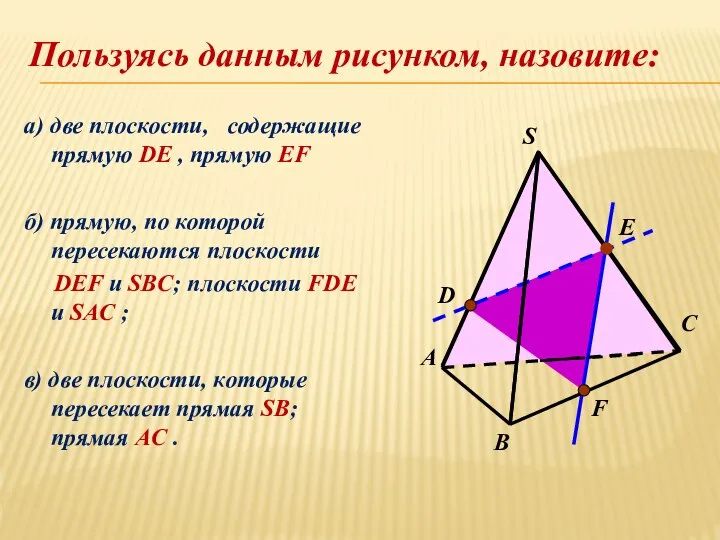
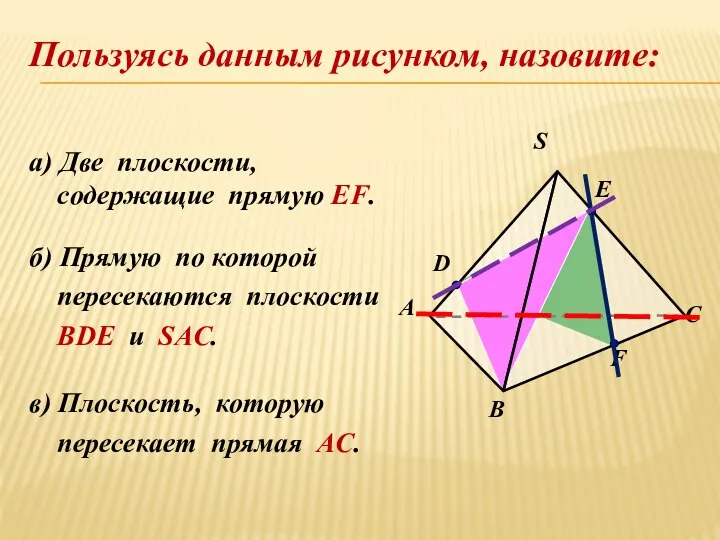
а) две плоскости, содержащие прямую DE , прямую EF
б) прямую, по которой пересекаются плоскости
DEF и SBC; плоскости FDE и SAC ;
в) две плоскости, которые пересекает прямая SB; прямая AC .
Пользуясь данным рисунком, назовите:

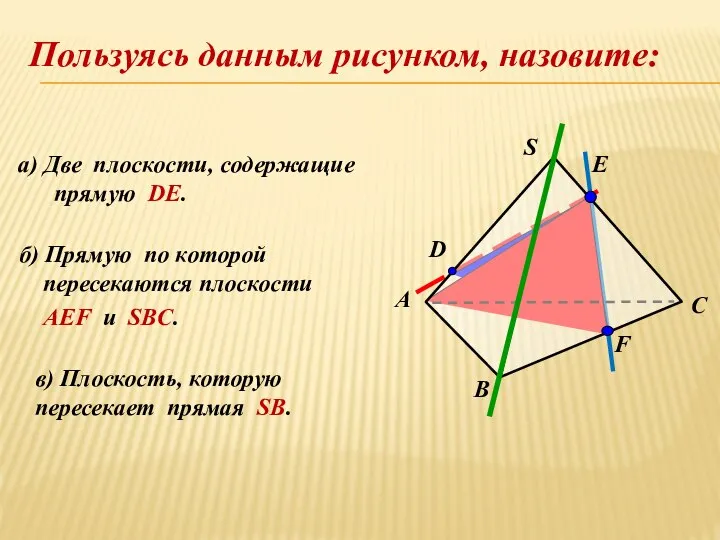
а) Две плоскости, cодержащие
прямую DE.
б) Прямую по которой пересекаются плоскости
АЕF и SBC.
в) Плоскость, которую пересекает прямая SB.
S
Пользуясь данным рисунком, назовите:

а) Две плоскости,
cодержащие прямую EF.
б) Прямую по которой
пересекаются плоскости BDЕ и SAC.
в) Плоскость, которую
пересекает прямая AC.
Пользуясь данным рисунком, назовите:

ДОМАШНЕЕ
ЗАДАНИЕ:
Выучить аксиомы.
2) П. 2-3
стр. 4 – 6.
3) № 1 (в, г); 2(в, г); 6.